Доказательство расходимости гармонического ряда

Доказательством на этой неделе будет сходимость гармонического ряда. Однако, прежде чем мы перейдем к этому, я представлю обычную еженедельную логическую головоломку.

Логическая головоломка

В понедельник в родильном отделении больницы находятся два младенца: мальчик и девочка.

Во вторник у ребенка появился новый малыш.

В среду случайным образом выбирают одного из младенцев. Это оказывается мальчик.

Какова вероятность того, что ребенок, родившийся во вторник, был мальчиком?

Доказательство расходимости гармонического ряда

Гармонический ряд — это множество обратных чисел ко всем целым числам. Другими словами, 1 1 , 1 2 , 1 3 , 1 4 ,6; font-family: 'Open Sans', sans-serif; color: #313131 !important;"> 1 5 ,…, 1 ∞ . Ряд называется расходящимся, если сумма всех его членов бесконечна. Это не очевидно в случае гармонического ряда, поскольку члены становятся бесконечно малыми. Однако позвольте мне доказать, что сумма действительно бесконечна.

Метод 1: Сравнительный тест

Если я могу доказать, что другой ряд с равным или меньшим числом членов расходится, то и гармонический ряд должен расходиться.

Гармонический ряд: 1 1 , 1 2 , 1 3 , 1 4 , 1 5 , 1 6 ,6; font-family: 'Open Sans', sans-serif; color: #313131 !important;"> 1 7 , 1 8 , 1 9 , 1 10 , 1 11 , 1 12 , 1 13 ,…, 1 ∞ .

Серия 2: 1 1 , 1 2 ,6; font-family: 'Open Sans', sans-serif; color: #313131 !important;"> 1 4 , 1 4 , 1 8 , 1 8 , 1 8 , 1 8 , 1 16 , 1 16 , 1 16 , 1 16 ,6; font-family: 'Open Sans', sans-serif; color: #313131 !important;"> 1 16 , 1 16 , 1 16 , 1 32 ,…, 1 ∞ .

Последовательность 2 начинается с тех же двух элементов, что и гармонический ряд. Затем, для каждого n>=2, она повторяется 1 / ²ⁿ × ^2n-1 раз. Заметим, что каждый элемент последовательности 2 равен или меньше элемента гармонического ряда. Последовательность 2 можно разбить на группы, сумма элементов которых равна 1 / ²ⁿ × ^2n-1 = 1/2 . Для наглядности, обозначим каждую группу разным цветом:

Серия 2: 1 1 ,6; font-family: 'Open Sans', sans-serif; color: #313131 !important;"> 1 2 , 1 4 , 1 4 , 1 8 , 1 8 , 1 8 , 1 8 , 1 16 , 1 16 , 1 16 , 1 16 ,6; font-family: 'Open Sans', sans-serif; color: #00A0D1 !important;"> 1 16 , 1 16 , 1 16 , 1 16 , 1 32 (16 раз), 1 64 (32 раза) …, 1 ∞

1 + ( 1 2 X ∞)= ∞

Метод 2: Математический анализ

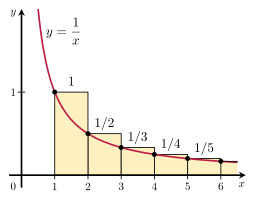
Обратите внимание, что площадь желтых прямоугольников больше, чем площадь под красной кривой. Площадь под красной кривой равна:

∫ ₁ ^∞ 1 x dx = ln(x) + c от 1 до ∞ = ln(∞) + c – ln(1) – c = ∞.

Решение логической головоломки

Краткий ответ

Существует два возможных объяснения произошедшего. Назовем их X и Y.

X = Мальчик появился во вторник, а в среду был замечен мальчик. Вероятность этого равна (1/2)*(2/3) = 2/6 = 1/3.

Y = Девочка появилась во вторник, а мальчик — в среду. Вероятность этого равна (1/2)*(1/3) = 1/6.

X + Y = 1/3 + 1/6 = 1/2

Вопрос сводится к тому, какова вероятность двух событий, где X — это то, что произошло. Вероятность будет X/(X+Y) = (1/3)/(1/2) = 2/3.

Развернутый ответ

Формула условной вероятности Байеса гласит, что Prob(A при условии B) = Prob(A и B)/Prob(B), где prob(x) = вероятность любого события x. Пусть:

А = Мальчик, добавлено во вторник

6; font-family: 'Open Sans', sans-serif; color: #313131 !important; ">B = Мальчик, замеченный в среду

В этом случае:

Вероятность (A при условии B) = Вероятность (мальчик добавлен во вторник при условии, что мальчик наблюдался в среду) = Вероятность (мальчик добавлен во вторник и мальчик наблюдался в среду) / Вероятность (мальчик наблюдался в среду).

Учитывая отсутствие информации о жеребьевке во вторник, существует 50% вероятность того, что во вторник родился мальчик. Если предположить, что ребенок, родившийся во вторник, был мальчиком, то вероятность того, что ребенок, родившийся в среду, также будет мальчиком, составляет 2/3.

Аналогично, учитывая отсутствие информации о жеребьевке во вторник, существует 50% вероятность того, что во вторник родилась девочка. Если предположить, что ребенок, выпавший во вторник, был девочкой, то вероятность того, что ребенок, выпавший в среду, будет мальчиком, составляет 1/3.

Вероятность того, что в среду выпал мальчик, равна: вероятность (мальчик добавлен во вторник) * вероятность (мальчик выпал в среду) + вероятность (девочка добавлена во вторник) * вероятность (мальчик выпал в среду) = (1/2) * (2/3) + (1/2) * (1/3) = 1/2.

Вероятность того, что мальчик был выбран во вторник, а мальчик — в среду, равна (1/2)*(2/3) = 1/3.

Таким образом, ответ равен (1/3)/(1/2) = 2/3.