Круговое планирование

Тема этой недели — как составить расписание кругового турнира. Прежде чем продолжить, поясню: круговой турнир — это формат турнира, в котором каждый игрок играет с каждым другим игроком. В турнире с n игроками количество матчей будет равно n(n-1)/2.

Легко перечислить все n(n-1)/2 возможных пар между n игроками. Однако в идеале это делать по раундам, когда каждый игрок играет один раз в каждом раунде. Вот как это сделать с четным числом игроков. Рассмотрим в качестве примера ситуацию с восемью игроками. На следующем изображении мы обозначим игроков от A до H и покажем двух игроков в матче в четырех прямоугольниках. Эти четыре игры составят первый раунд. Обратите внимание, как играют все.

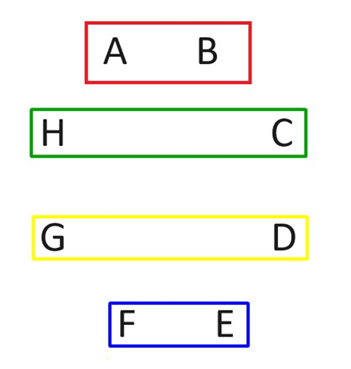
Во втором раунде оставьте игрока А на том же месте. Затем поверните всех остальных по часовой стрелке, как показано на следующей схеме.

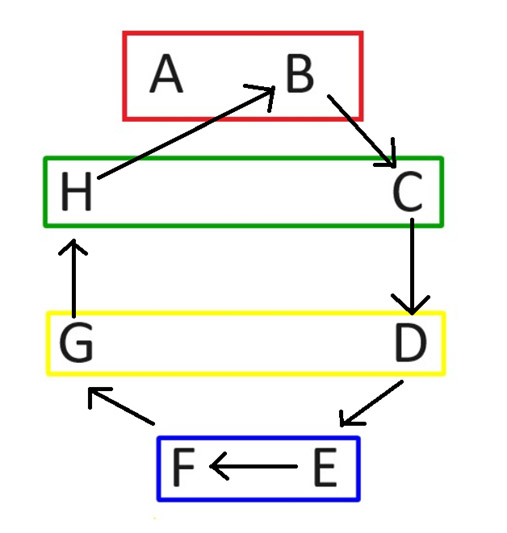
После ротации второй раунд матчей будет выглядеть следующим образом:

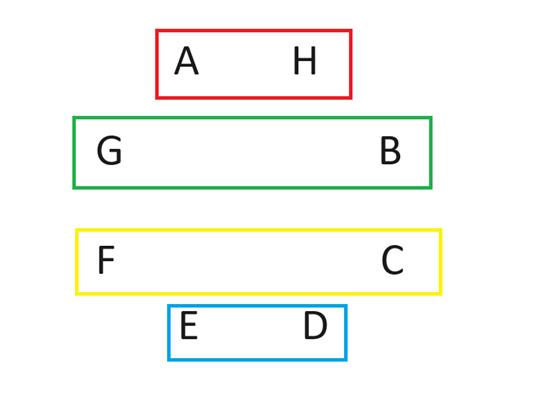
Продолжайте в том же духе, пока все не сыграют против игрока А. Я не могу объяснить, почему это работает, но это так. Это работает для любого четного числа игроков. Для более подробного обсуждения поищите «метод круга» и «круговая система».

В следующей таблице показаны все пары игроков в случае с восемью участниками. Обратите внимание, что каждый игрок играет с каждым из остальных ровно один раз.

Круглый	Игрок 1	Игрок 2
1	А	Б
1	ЧАС	С
1	Г	Д
1	Ф	Е
1	А	ЧАС
2	Г	Б
2	Ф	С
2	Е	Д
3	А	Г
3	Ф	ЧАС
3	Е	Б
3	Д	С
4	А	Ф
4	Е	Г
4	Д	ЧАС
4	С	Б
5	А	Е
5	Д	Ф
5	С	Г
5	Б	ЧАС
6	А	Д
6	С	Е
6	Б	Ф
6	ЧАС	Г
7	А	С
7	Б	Д
7	ЧАС	Е
7	Г	Ф

Если количество игроков нечётное, просто добавьте в турнир фиктивного игрока, чтобы получить чётное число. Тот, кто играет против фиктивного игрока, получает пропуск этого раунда. Таким образом, у каждого игрока будет один раунд, в котором он пропускает игру. Вот как это будет выглядеть в турнире с семью игроками.

Круглый	Игрок 1	Игрок 2
1	А	Б
1	пока	С
1	Г	Д
1	Ф	Е
2	А	пока
2	Г	Б
2	Ф	С
2	Е	Д
3	А	Г
3	Ф	пока
3	Е	Б
3	Д	С
4	А	Ф
4	Е	Г
4	Д	пока
4	С	Б
5	А	Е
5	Д	Ф
5	С	Г
5	Б	пока
6	А	Д
6	С	Е
6	Б	Ф
6	пока	Г
7	А	С
7	Б	Д
7	пока	Е
7	Г	Ф

Наконец, предположим, что это теннисный турнир, где у каждого корта есть хорошая и плохая сторона. Плохая сторона, вероятно, может быть обращена к солнцу. Как справедливо обеспечить каждому игроку одинаковое количество раз игрового времени на хорошей и плохой сторонах корта?

Для решения этой проблемы я предлагаю использовать « расширение Спока-ящера », как это объясняется в «Теории большого взрыва». Этот метод игры в камень-ножницы-бумага работает с любым нечетным числом символов. Чтобы справедливо определить, какому игроку достанется хорошая сторона, рассмотрим случай с семью игроками. На следующей диаграмме показано, как игрок получает хорошую сторону, что показано стрелкой, указывающей на игрока, получившего плохую сторону.

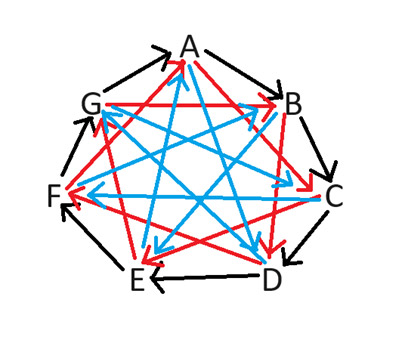
Например, если бы игроки B и D играли, B получил бы преимущество, потому что стрелка между ними указывает на D. Нетрудно понять, как я нарисовал диаграмму. Стрелки всегда указывают по часовой стрелке. Их нужно нарисовать для каждого возможного количества промежутков от 1 до 3.

Однако рисовать такую диаграмму не нужно, достаточно лишь кольца из букв. Рассмотрим оба способа движения по кругу по часовой стрелке, чтобы перейти от одного игрока к другому. Способ с меньшим количеством шагов позволит получить выигрышную сторону. Рассмотрим игру между B и F. Двигаясь по часовой стрелке, от B до 4 нужно сделать четыре шага, а от F до B — три. Поскольку три меньше четырех, выигрышную сторону получает F.

В таблице ниже показаны все возможные пары участников в круговом турнире с участием семи игроков, включая распределение игроков по сторонам (хорошие и плохие стороны).

Круглый	Хорошая сторона	Плохая сторона
1	А	Б
1	С	пока
1	Д	Г
1	Е	Ф
2	А	пока
2	Г	Б
2	С	Ф
2	Д	Е
3	Г	А
3	Ф	пока
3	Б	Е
3	С	Д
4	Ф	А
4	Е	Г
4	Д	пока
4	Б	С
5	Е	А
5	Д	Ф
5	Г	С
5	Б	пока
6	А	Д
6	С	Е
6	Ф	Б
6	Г	пока
7	А	С
7	Б	Д
7	Е	пока
7	Ф	Г

К сожалению, эта стратегия балансировки сторон не работает для четного числа игроков. Это связано с тем, что расстояния по кругу одинаковы, когда два игрока находятся на противоположных сторонах. При необходимости этот метод можно использовать для всех остальных ситуаций, но тогда игрокам придется выбирать случайным образом, когда они окажутся на расстоянии 180 градусов друг от друга по кругу.

На этом я пока остановлюсь. Я оставляю за собой право подробнее обсудить эту тему в одном из будущих выпусков информационного бюллетеня. Возможные темы для дальнейшего обсуждения — матчи с участием трех и более игроков, а также использование нескольких кортов, когда желательно сбалансировать частоту игры каждого игрока на каждом корте.

В заключение, желаю всем счастливой Хануки!

Автор: Michael Shackleford