Теорема о том, что сумма углов треугольника равна 180 градусам.

Общеизвестно, что сумма внутренних углов любого треугольника равна 180 градусам. В этом выпуске я представлю простое доказательство. Однако перед этим я приведу обычную еженедельную логическую головоломку.

Логическая головоломка

У короля 49 золотых монет. Каждая монета весит 1, 2, 3, ... 49 граммов. Как он может разделить их между семью сыновьями так, чтобы каждый сын получил по семь монет, сумма весов которых будет равна?

Доказательство того, что сумма внутренних углов любого треугольника равна 180 градусам.

Начну с того, что нарисую произвольный треугольник и обозначу его углы.

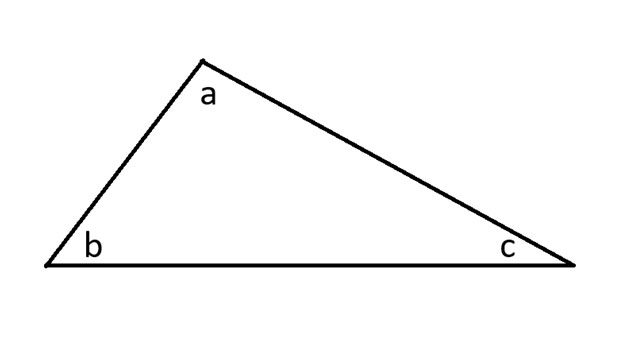
Далее я проведу все три стороны треугольника, а также параллельную линию, которая касается угла А.

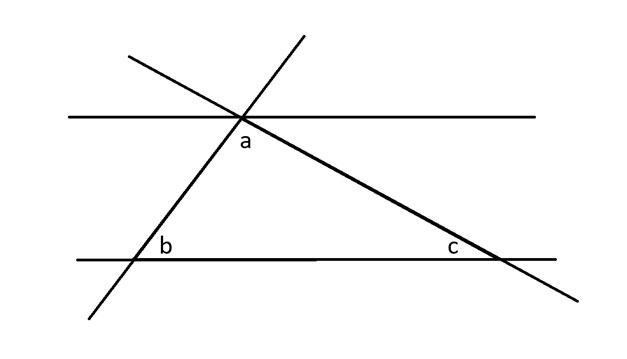
Далее я применю теорему о противоположных углах к углу b, которая гласит, что углы в противоположных точках двух пересекающихся линий равны.

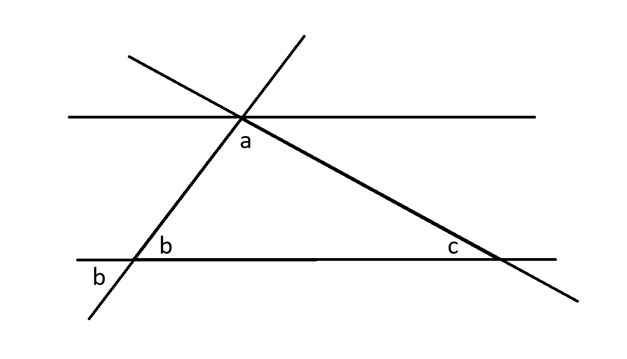
Когда диагональ пересекает набор параллельных линий, она образует одинаковые углы в местах пересечения с каждой из них. Я использую это, чтобы показать еще один угол b градусов рядом с углом a. Затем я делаю то же самое с углом c.

6; font-family: 'Open Sans', sans-serif; color: #313131 !important; ">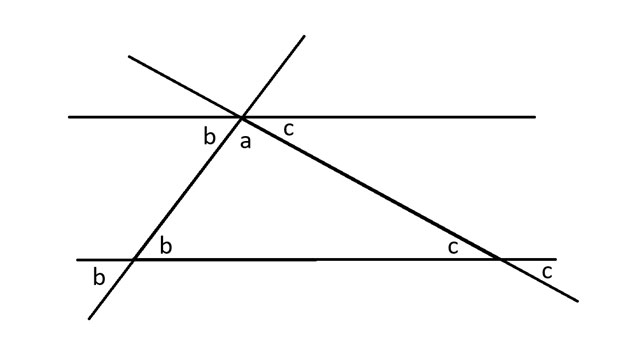

В окружности 360 градусов. Следовательно, в полукруге 180 градусов. Другими словами, если посмотреть на углы в нижней точке верхней параллельной линии, то a + b + c = 180 градусов. Это также три угла исходного треугольника. Таким образом, сумма углов треугольника равна 180 градусам.

Решение логической головоломки

Создайте магический квадрат и раздайте каждому сыну монеты в любом столбце. Вы также можете разделить монеты по рядам. «Как создать магический квадрат 7х7?», — можете спросить вы. Следующий способ известен как сиамский метод и был открыт в Индии давным-давно.

Начнём с сетки, обозначенной как игровое поле для морского боя 7x7.

Начните с цифры 1 в ячейке A4. Затем следуйте этим правилам:

1. При следующей ставке всегда прибавляйте 1 к предыдущему числу.
2. Всегда двигайтесь в северо-западном направлении, если только это место не занято или вы уже находитесь в ряду А или столбце 7.
3. Если вы находитесь в строке А, то для следующего номера перейдите в столбец G.
4. Если вы находитесь в 7-м столбце, то для следующего числа перейдите в 1-й столбец.
5. Вызов A7 приведет к зацикливанию сигнала в обоих направлениях до G1.
6. Если следующая клетка, на которую вам следует перейти, занята, то перейдите на следующую клетку, соответствующую следующему числу (она должна быть пустой).

Вот как мы начнём:

1. 1 в ячейке A4.
2. Мы находимся в строке А, поэтому переходим к строке G, помещая цифру 2 в ячейку G5.
3. Затем мы поставили 3 в F6 и 4 в E7.
4. Мы находимся в 7-м столбце, поэтому мы делаем круговой ход, помещая цифру 5 в ячейку D1.
5. Вставьте 6 в C2, 7 в B3.
6. Далее мы подошли бы к ячейке A4, но она занята цифрой 1. Поэтому мы опускаемся ниже и ставим следующую цифру, 8, в ячейку C3.
7. Повторяйте эти действия, пока Волшебный квадрат не заполнится.

Вот как это будет выглядеть после завершения:

jpg" />

Этот метод подойдет для любого магического квадрата с нечетными размерами.

Затем решите, будете ли вы делить по строкам или по столбцам. Каждому сыну достанутся монеты, найденные в одной из строк/столбцов. Например, если вы будете делить по столбцам, сыну 1 достанутся монеты № 30, 38, 46, 5, 13, 21 и 22.