Доказательство суммы первых n целых чисел

На этой неделе я приведу одно из своих самых простых доказательств: 1+2+3+…+n = n(n+1)/2. Я покажу это двумя очень наглядными способами. На данный момент это моё самое простое доказательство. Однако, прежде чем мы перейдём к нему, я представлю свою обычную еженедельную логическую головоломку.

Логическая головоломка

Элис, Боб и Коул делают следующие заявления:

1. • Элис: Боб — лжец.
2. • Боб: Коул — лжец.
3. • Коул: Элис и Боб — лжецы.

Все трое либо всегда говорят правду, либо всегда лгут. Все они знают, правдива ли речь двух других. Кто же говорит правду?

Ответ и решение вы найдете в конце информационного бюллетеня.

Доказательство суммы первых n целых чисел

Всем известно, что сумма первых n целых чисел равна n(n+1)/2. Другими словами, 1+2+3+…+n = n(n+1)/2. Я приведу два простых доказательства того, почему это так.

Метод 1

Легко заметить, что среднее число в последовательности равно (n+1)/2. Количество членов ряда равно n. Сумма равна произведению количества членов и среднего члена = n × (n+1)/2 = n(n+1)/2.

Этот же метод можно использовать для нахождения суммы с любой начальной и конечной точкой. Назовем начальное число a, а конечное число b. Среднее арифметическое будет равно (a+b)/2. Количество слагаемых будет равно (a-b+1).Таким образом, сумма всех чисел в ряду будет равна (a-b+1) × (a+b)/2.

Метод 2

Следующий метод проще объяснить наглядно. Рассмотрим следующую диаграмму, где синие квадраты иллюстрируют целые числа от 1 до 5.

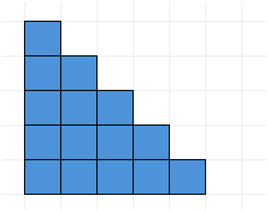
Далее, продублируйте его и разместите рядом с исходным фрагментом следующим образом, образовав прямоугольник.

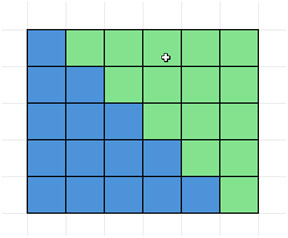
Обратите внимание, что размеры прямоугольника выше равны 5 × 6. В общем случае, при сложении целых чисел от 1 до n, размеры равны n × (n+1). Затем разделим эту площадь на 2, поскольку мы ищем площадь только одной из двух частей. Таким образом, площадь одной части равна n(n+1)/2.

Решение логической головоломки

У всех троих есть два возможных состояния: говорить правду или лгать. Таким образом, получается ^2³ = 8 вариантов. Все они перечислены в таблице ниже.

Сценарий	1	2	3	4	5	6	7	8
Алиса	Т	Т	Т	Т	Ф	Ф	Ф	Ф
Боб	Т	Т	Ф	Ф	Т	Т	Ф	Ф
Коул	Т	Ф	Т	Ф	Т	Ф	Т	Ф

Обратите внимание, что Боб и Коул называют друг друга лжецами. Это возможно только в том случае, если один из них говорит правду, а другой лжец. Таким образом, мы можем исключить четыре ситуации, в которых Боб и Коул одинаково правдивы. Остаются сценарии 2, 3, 6 и 7. Давайте рассмотрим их по очереди.

Во втором сценарии указано, что Алиса говорит правду. Её правдивое утверждение делает Боба лжецом. Однако Боб в этом сценарии тоже говорит правду, что приводит к противоречию. Таким образом, второй сценарий отпадает.

В третьем сценарии предполагается, что Алиса говорит правду. Она говорит, что Боб лжец, что соответствует предположениям третьего сценария. Однако Коул указан как правдивый человек, который говорит, что Алиса лжет. Алиса не может быть одновременно правдивой и лживой, поэтому третий сценарий отпадает.

В седьмом сценарии предполагается, что Алиса лжет. Она говорит, что Боб лжец, что правда. Однако это сделало бы Алису правдивой. Алиса не может быть одновременно правдивой и лживой, поэтому седьмой сценарий отпадает.

Остается только шестой сценарий. Давайте убедимся, что он работает. Если бы Алиса была лжецом, это сделало бы Боба правдивым. Если бы Боб был правдивым, то Алиса, Боб или оба были бы правдивыми. Боб правдив, поэтому утверждение Коула ложно. Таким образом, оно имеет смысл. Боб — единственный правдивый человек.