Анализ парных квадратов - Дополнительная ставка в блэкджеке

Привет, это Майк. Цель этого видео — показать, как рассчитать возврат игроку за дополнительную ставку «Пара в квадрате» в блэкджеке . Прежде чем перейти к «Ставке на сет», также известной как «Пара в квадрате», позвольте мне быстро рассказать о паре математических функций, которые вам, возможно, уже известны. n-факториал — это количество способов расположить n различных уникальных элементов.

Это просто произведение всех целых чисел от единицы до n .

Например:

Пять факториалов — это количество способов расположить пять разных предметов, что равно 1×2×3×4×5, то есть 120. Позвольте мне также объяснить функцию сочетаний. Это количество способов выбрать Y предметов из X, в данном конкретном примере, без учета порядка.

Например, сколько раз в ресторане El Pollo Loco вы сможете выбрать три уникальных гарнира из восьми доступных вариантов.

Эта функция...

...равно факториалу X, деленному на факториал Y, деленному на факториал X минус факториал Y. Я объяснил, почему это так, в своем видео о вероятностях в покере. В качестве примера можно привести вопрос: сколько существует способов выбрать пять карт из 52?

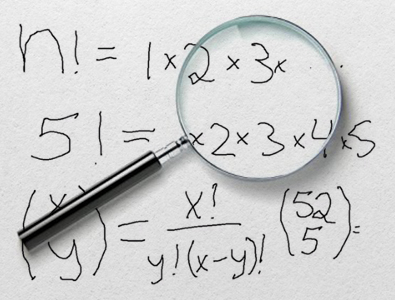
Это равно 52 факториалу, деленному на пять факториалов, деленному на 47 факториалов, что равно 2 598 960. Теперь, когда с этим разобрались, перейдем ко второй части, где я рассчитаю комбинации каждого возможного исхода ставки «Пара квадратов».

Готовы перейти к следующему шагу:

Задача состоит в том, чтобы вычислить количество комбинаций каждого возможного исхода этой ставки. В этом и заключается суть всего видео . Предположим, у нас шесть колод карт. Для пары мастей в колоде 52 разные карты. 13 рангов, умноженные на четыре масти, равны 52. Обе пары должны быть одинаковыми.

Например, обе карты должны быть пятеркой бубен. После того, как вы выбрали свою конкретную карту, в колоде из шести карт будет шесть таких карт.

Вы должны выбрать две карты из этих шести. Шесть выбирают две = 15, поэтому 52 умножить на 15 равно 780. Существует 780 способов получить выигрышную пару одной масти. Сколько существует способов получить непарную пару? Ну, во-первых, вы должны выбрать ранг непарной пары, например, пятерки.

Тогда вам нужно выбрать две разные масти для этой пары, потому что они должны быть разными. Если бы они были одинаковыми, то у вас была бы парная одежда, и вы выиграли бы больше денег.

Есть четыре способа выбрать две масти из четырех, что в сумме составляет шесть. Затем, после того как вы выбрали свой ранг и две масти, есть шесть способов выбрать каждую из них из шести колод.

Например:

Если ваши две карты — король треф и король пик, то в колоде из шести карт содержится по шесть каждой из них. 13 умножить на шесть умножить на шесть в квадрате равно 2808. Наконец, проиграть эту ставку можно, если не собрать пару.

Сколькими способами можно не получить пару?

Итак, вам нужно будет выбрать два разных ранга из 13 доступных, например, семерки и десятки. Затем, после того как вы выберете два конкретных ранга, в колоде будет по 24 карты каждого из этих рангов.

Поскольку в каждой колоде по четыре карты определённого ранга, а всего в колоде шесть колод, то, например, всего в колоде 24 туза. Если бы у нас были, скажем, тузы и короли, то было бы 24 туза и 24 короля.

Вы выбираете по одному из каждой из этих групп.

13 выбрать два — это 78 умножить на 24 в квадрате, что равно 44 928, так что вот наши комбинации. Далее перенесем все это в Excel, чтобы посмотреть, какую выгоду мы получаем от ставки «Пара квадратов».

Перейдём к заключительной части...

Я только что показал вам количество комбинаций каждого возможного исхода в ставке «Пара квадратов». Наиболее распространенная таблица выплат, которую вы видите при игре с шестью колодами, — это выплата за пару одномастных карт 15 к 1, а за пару разномастных карт — 10 к 1.

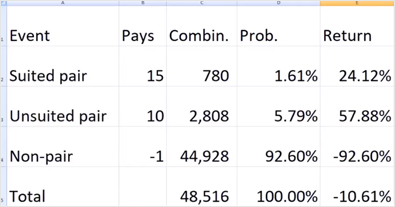
Давайте рассчитаем вероятность каждого события — это очень просто.Вероятность образования пары одномастных карт равна числу способов составить пару одномастных карт, деленному на общее число способов выбрать две карты из 312 и колоды, которое составляет 40 516. 780, разделенное на 40 516, дает примерно 1,61%.

Используя ту же формулу — количество комбинаций каждого события, деленное на общее число, — мы получаем следующие вероятности: 5,79% — вероятность выпадения неподходящей пары и 92,6% — вероятность получения двух разных рангов.

Следующий...

...Мой способ анализа ставки — это просто умножить выигрыш на вероятность. Выигрыш от одномастной пары составляет 15 умножить на вероятность выигрыша, то есть 1,61%, что в сумме дает — давайте увеличим это значение для вас, 24,12%. Используя ту же формулу, мы видим, что выигрыш от непарной пары составляет 57,88%, а выигрыш от непарной пары — -92,6%.

Это означает, что если игрок... это доллар.

Например: он может рассчитывать получить обратно 24,12 цента от одномастных пар, 57,8 цента от разномастных пар, но потерять 92,6 цента от непарных карт. Чтобы получить общую выгоду для игрока , мы просто суммируем эти значения и получаем -10,61%.

Это значит...

Игрок может рассчитывать на потерю 10,61% от всех денег, поставленных на парную игру. Иными словами, преимущество казино составляет 10,61%. Другими словами, за каждый поставленный доллар игрок может рассчитывать на возврат примерно 89,39 центов, а 10,61 цента достается казино.

Для сравнения: преимущество казино в блэкджеке может составлять всего 0,28%. Даже при плохих правилах оно ближе к 0,6%. В данном случае, при условии, что выплата за блэкджек составляет три к двум (к чему следует стремиться при каждой возможности), преимущество казино достигает почти 11%.

Это лишь подтверждает то, что я говорил уже тысячи раз: дополнительные ставки — это ставки для простаков. И это прекрасный тому пример. Я рекомендую избегать этой дополнительной ставки, как и любых других, если это возможно.

Спасибо за просмотр, ребята, и увидимся в моём следующем видео!

Автор: Michael Shackleford