Вероятности в пятикарточном стад-покере

Привет, это Майк, и цель этого видео — показать вам, как рассчитать вероятности в пятикарточном стад-покере . Другими словами, какова вероятность составления любой заданной покерной комбинации из пяти случайных карт из 52? Прежде чем ответить на вопрос о количестве комбинаций каждой покерной комбинации, позвольте мне задать вам более простой вопрос, и если вы знаете, как получить ответ, можете пропустить этот шаг.

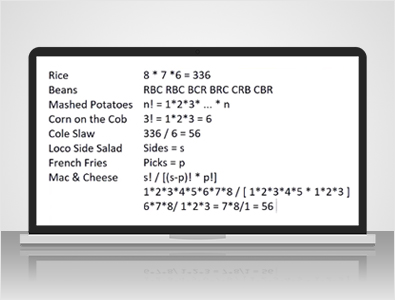
В El Pollo Loco:

У них есть восемь так называемых классических гарниров, которые я перечислил слева. Также есть несколько гарниров класса люкс, но я не буду этим усложнять. Если вы заказываете набор из 12 кусочков, вы можете выбрать любые три из этих восьми гарниров. Давайте представим, что вам нужно выбрать три разных блюда.

Вопрос в том...

...сколькими способами можно заказать три разных гарнира из восьми? Другими словами, предположим, что вы ходите туда каждый день и каждый день заказываете три разных гарнира. Сколько дней вы сможете обходиться без повторения одних и тех же трех гарниров?

Если бы порядок, в котором вы их заказали, имел значение, то ответ был бы 8 x 7 x 6, потому что есть восемь способов выбрать первый товар, семь способов выбрать второй и шесть способов выбрать третий, но кассиру это неважно. Порядок, в котором вы их заказали.

Если вы скажете -

«Я хочу рис, фасоль и кукурузу», — вы получите одно и то же, независимо от того, скажете вы «рис, фасоль и кукурузу» или «кукурузу, фасоль и рис». Сколько разных способов можно заказать три разных гарнира? Допустим, вам нравятся рис, фасоль и кукуруза. Вы можете заказать их в таком порядке: рис, кукуруза, фасоль; фасоль, кукуруза, рис; фасоль, рис, кукуруза или кукуруза, рис, фасоль или кукуруза, фасоль, рис — всего шесть возможных вариантов.

Как я узнал, что их шесть, не просто записав?

Ну, есть очень простая формула . Если там N предметов, то количество способов их упорядочить равно 1 x 2 x 3 раз, и так далее до N.

В данном случае вопрос заключался в том, сколькими способами можно расположить три предмета? Ответ: 3! Это 1 x 2 x 3, что равно 6. Из 336 способов расположить три предмета из восьми возможных, разделив на шесть, поскольку существует шесть способов расположить каждую комбинацию, получаем 56.

Вы можете спросить: какова же общая формула?

Если, допустим, количество сторон равно S, а количество разрешенных вариантов выбора равно P, то общая формула для количества способов выбрать P предметов из S — s! / s - p! xp!. Позвольте мне показать, что это работает на примере задачи.

В этом случае:

s = 8, поэтому 8! равно 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8, а в знаменателе у нас s - p, или 8 - 3, что равно 5 или 5!. Таким образом, 1 x 2 x 3 x 4 x 5, а также p! или 3!, что равно 1 x 2 x 3. Вы видите, что 1 x 2 x 3 x 4 x 5 равно 120, и это в числителе и знаменателе, поэтому давайте сократим это, оставив нам 6 x 7 x 8 / 1 x 2 x 3. Что ж, 2 x 3 = 6, и шестерка присутствует как в числителе, так и в знаменателе, поэтому давайте разделим это.

В итоге у нас остаётся лишь...

...7 x 8 / 1, что равно 56. Для целей этого видео позвольте мне представить функцию. Мы назовем эту функцию C от x и y, как число способов выбрать y предметов из x, или, как мы бы сказали математически, x выбирает y, и определим ее как x! / x - y! умножить на y!.

В случае с примером El Pollo Loco, если бы вопрос звучал так:

«Сколькими способами можно выбрать три слайда из восьми?»

Мы бы выразили это так, что будет равно — перестановка равна 56. Думаю, мы наконец-то готовы начать говорить о покере. Сколько существует способов выбрать пять карт из 52? Ну, это будет 52 выбрать 5, что равно 52! / 47!, 47, потому что 52 - 5 x 5!, и это равно 2 598 960. Давайте начнем с роял-флеша.

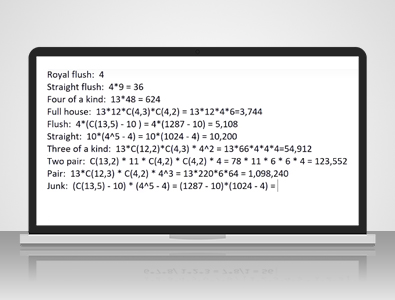
Ну, это довольно просто. Для роял-флеша существует четыре масти: червы, пики, трефы и бубны.В колоде должно быть десять мастей: Валет, Дама, Король, Туз. Да, есть всего четыре варианта. Роял и червы, бубны, трефы или пики.

А как насчет прямого слива?

Итак, у нас по-прежнему четыре масти, но стрит-флеш может начинаться с туза, то есть туз, двойка, тройка, четверка, пятерка (также известный как колесный стрит-флеш), и заканчиваться девяткой, десяткой, валетом, дамой, королем. Если бы это были десятка, валет, дама, король, туз, то это был бы роял-флеш. Самая младшая карта может быть любой от туза до девятки.

В этом случае...

...туз считается за единицу. Для стрит-флеша существует девять возможных комбинаций карт, поэтому 4 масти x 9 комбинаций = 36. Для каре существует 13 возможных рангов для каре, например, дамы, и затем в колоде остается 48 карт для синглтона после того, как вы вынете четыре карты для каре. Это равно 624.

Для полного зала

Для тройки существует 13 возможных рангов, а для пары — 12. Для тройки есть четыре варианта выбора, три способа выбрать три масти из четырех, умноженные на четыре варианта выбора, и два способа выбрать две масти из четырех для пары. Это равно 13 x 12 x 4 x 6, что равно 3744. Что касается флеша, то для флеша у нас четыре масти.

Сколькими способами можно выбрать пять рангов из 13 в данной масти?

Итак, это будет 13, выбираем 5, но 10 из этих способов приведут к стрит-флешу или роял-флешу. Например, 5, 6, 7, 8, 9 приведут к стрит-флешу, поэтому нам нужно выбрать эти 10 пар рангов, которые идут подряд. Таким образом, 13, выбираем 5, получаем 1287, вычитаем 10 и умножаем на 4, получаем 5108.

А как насчет прямой дороги?

Итак, как мы только что видели на примере флеша, существует 10 возможных комбинаций для стрита, начиная с туза, двойки, тройки, четверки, пятерки и заканчивая десяткой: валет, дама, король, туз. Для каждой карты, для каждого ранга в этом стрите, существует четыре возможных масти. 4 х 4 х 4 х 4 х 4 = 4^5, количество способов выбрать другую масть для каждой из пяти карт. Если мы выберем одну и ту же масть все пять раз, то у нас также останется стрит-флеш или роял-флеш. Нам нужно вычесть эти значения. 4^5 = 1024 - 4 = 10200 способов составить стрит.

А как насчет тройки одинаковых карт?

Итак, существует 13 способов выбрать ранг для тройки, а затем нужно выбрать два ранга из оставшихся 12 для двух одиночных карт. После этого нужно выбрать четыре масти из трех для тройки, а затем по одной масти из четырех для каждой из двух одиночных карт.

У нас осталось 13 способов выбрать ранг для тройки одинаковых карт. Из оставшихся 12 способов выбрать два ранга для двух одиночных карт существует 66 способов выбрать три масти из четырех для тройки одинаковых карт, а также четыре способа выбрать одну масть для двух одиночных карт. Ответ — 54 912.

А как насчет двух пар?

Итак, есть 13 способов выбрать два ранга из 13 для вашей пары, тогда у вас останется один ранг для одиночной карты. Для каждой пары есть четыре способа выбрать две масти из четырех для вашей пары. Для вашей одиночной карты четыре масти. 13 способов выбрать два равны 78 умножить на шесть умножить на шесть умножить на четыре, равно... я забыл свои 11 рангов для одиночной карты. 78 x 11 x 6 x 6 x 4 = 123 552.

Для пары

Существует 13 способов выбрать ранг пары, затем нужно выбрать три ранга из двенадцати оставшихся для трех одиночных карт. Для вашей пары есть четыре способа выбрать две масти из четырех, затем для каждой из трех одиночных карт есть четыре возможных масти на выбор. 4 x 4 x 4 — это количество способов выбрать три масти для ваших трех одиночных карт, что равно 13 x 12 — 12 способов выбрать три масти, равно 220 x 6 x 4³ = 64 = 1 098 240.

Окончательно

Давайте рассчитаем вероятность того, что туз окажется выше или ниже, что я назову просто «мусором». Чтобы получить «мусор», нужно выбрать пять разных рангов из 13. Есть 13 способов выбрать пять рангов из десяти, но, как мы видели на примере флешей, нужно выбрать десятые пары, образующие стрит. После того, как вы выбрали пять непоследовательных рангов, для каждого из рангов есть четыре возможных масти.

Вы берете четыре в пятой степени...

...Как мы видели на примере стрейта, нам нужно вычесть четыре, чтобы получить количество способов выбрать одну и ту же масть каждый раз, что приведет к флешу. 13 выбрать пять равно 1287 минус 10 для стрейта, умноженное на четыре в пятой степени, равно 1024 минус четыре равно 1 302 540.

Следующий

Давайте всё это перенесём в электронную таблицу. Я быстро покажу вам, как это сделать в Excel. Мы уже видели, что существует всего четыре способа получить роял-флеш, по одному для каждой масти, 36 стрит-флешей, четыре масти умножить на девять возможных комбинаций. Для вашей каре есть 13 рангов на выбор: четыре, четыре каре и 48 карт остаются для синглтона. Для фулл-хауса есть 13 рангов для трио и 12 для пары.

Четверо выбирают три способа выбрать масти для тройки одинаковых карт. Четверо выбирают два способа выбрать две масти из четырех для пары. В Excel эта формула выражается с помощью распространенной формулы, объединяющей большие числа и запятые, как я и написал. Это дает нам число 3744, которое мы получили ранее.

Для смыва

Есть четыре масти на выбор, 13 выбирают пять способов, пять рангов из 13 в этой масти минус 10 последовательностей, которые приведут к стрит-флешу или роял-флешу, потому что они идут подряд. Это дает нам 5108 флешей. Для стрита есть 10 возможных последовательностей, четыре масти для каждой карты в последовательности, но вычитаем четыре для четырех мастей, которые приведут к стрит-флешу или роял-флешу, и получаем 10200.

Для трех одинаковых

Существует 13 рангов, для тройки одинаковых карт 12 выбирают два ранга для двух одиночных карт. Четыре выбирают три способа выбрать три масти из четырех и четыре раза четыре способа выбрать две масти для двух одиночных карт. 554 912, тройка одинаковых карт. Для двух пар существует 13 способов выбрать два ранга из 13 для двух пар. 11 остаются для одиночной карты, четыре выбирают два способа выбрать две масти из четырех для двух пар и четыре масти для одиночной карты.

Для пары у нас есть 13 рангов, 12 выбирают три способа из 12 для трех одиночных карт. Четыре выбирают два способа из четырех для пары и четыре в третьей степени для способов выбора трех мастей для трех одиночных карт.

Наконец, перейдём к хламу.

Существует 13 способов выбрать пять рангов из 13, за вычетом 10 последовательных способов, которые дадут вам стрит, и четыре способа выбрать каждую из мастей. Четыре в пятой степени минус четыре для способов, которые дадут вам флеш. Как видите, сумма всех этих чисел составляет 2 598 960, что мы также получили в начале этого видео. Хорошо, давайте перейдем к практическому применению всего этого.

Одна из сотен игр казино , которые я описываю на своем сайте Wizard of Odds, называется : Let it ride .

Давайте откроем эту страницу, и перед вами игра в покер, основанная на пятикарточной комбинации. Здесь нет розыгрыша карт, все основано на пяти случайных картах из 52. Я не буду вдаваться в подробности правил, но есть дополнительная ставка, которая выплачивается в зависимости от покерной ценности ваших пяти карт.

Вы можете увидеть...

...я перечислил здесь девять возможных таблиц выплат, но четвертая таблица довольно распространенная. Я уже перевел ее в эту таблицу, ставка составляла 1 доллар. Если у вас роял-флеш, вы выигрываете 20 000 долларов, стрит-флеш — 20 000 долларов, четыре одинаковые карты — 400 долларов. Эти выплаты, кстати, основаны на соотношении 4 к 1, то есть вы не сохраняете свою первоначальную ставку, если выигрываете.

Вот все комбинации, для которых я уже рассчитал вероятности, а в столбце «Возврат» представлено произведение выигрыша на вероятность.

Например, существует:

Как мы уже знали, вероятность собрать роял-флеш составляет примерно четыре целых две десятых миллиона. Если умножить эту вероятность на 20000, получится ожидаемый выигрыш в 3,08 цента. Именно столько игрок может получить, поставив доллар, в виде выигрыша за роял-флеш. За стрит-флеш он может получить до 2,77 цента и так далее.

Если произвести все необходимые расчеты, то в итоге окажется, что игрок, сделавший ставку в 1 доллар, может рассчитывать получить обратно 74,4667 цента. Другими словами, за этот доллар игрок может рассчитывать получить обратно около 74 центов.47%, а казино оставит себе 25,53%.

Вот как бы я это выразил...

... преимущество казино составляет 25,53%, так что просто задумайтесь об этом на минуту. Казино забирает себе более 25% от этой ставки, что лишь подтверждает то, о чем я говорю уже более 20 лет: все дополнительные ставки — это ставки для простаков. Если вы усвоите из этого видео хотя бы одну вещь, я надеюсь, это будет именно она. Видео и так достаточно длинное, приношу свои извинения за продолжительность, и я надеюсь, что оно было информативным и вы чему-то научились.

Спасибо за просмотр.

Автор: Michael Shackleford