Видео о вероятности идеальной скобки

Привет, это Майк, и в этом видео я попытаюсь ответить на вопрос: какова вероятность заполнить идеальную турнирную сетку March Madness?

Я предполагаю, что у вас уже есть базовые знания о том, как это работает , но вкратце, в турнире на выбывание участвуют 64 баскетбольные команды; это означает, что всего будет 63 игры.

Турнир делят на четыре дивизиона , и в каждом дивизионе в первом раунде команда с первым номером посева играет с командой с 16-м номером, вторая команда — с 15-м, третья — с 14-м и так далее. Затем берут победителей всех игр первого раунда, и они играют друг с другом во втором раунде, и в итоге остается только один победитель.

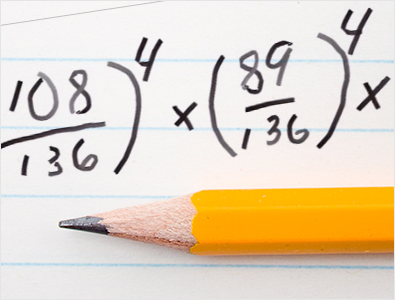
Теперь каждый март...

...в СМИ постоянно всплывает вопрос о вероятности заполнения идеальной турнирной сетки, и у меня мурашки по коже, когда я слышу цифру 1 к 9 квинтиллионам, 223 квадриллионам, 372 триллионам, 36 миллиардам, 854 миллионам, 781 000; я в это верю. Это просто вероятность правильного предсказания результатов 63 подбрасываний монеты подряд. Я не думаю, что кто-то заполняет турнирную сетку March Madness таким образом, потому что некоторые команды явно лучше других. Например, команда с первым номером посева явно лучше, чем команда с шестнадцатым номером.

Прежде чем продолжить...

...позвольте мне сказать, что это видео было снято в апреле 2018 года, поэтому оно основано на всех играх «Мартовского безумия», сыгранных с 1985 по 2018 год. Хорошо, я также хотел бы затронуть другое видео на YouTube от профессора Джеффа Бергена . Он говорит, что при использовании некоторой стратегии, которую он не раскрывает, вероятность составления идеальной турнирной сетки составляет 1 к 128 миллиардам. Эта цифра довольно близка к той, которую получаю я.

Я бы предложил профессору Бергену подробнее рассказать, как он получил эту цифру, но я расскажу вам, как получил свою. Моя стратегия очень проста. Вы всегда выбираете команду с более высоким рейтингом в каждой игре, и в итоге у вас останется всего четыре команды с первым номером посева, после чего вы можете выбирать случайным образом.

Прежде чем кто-нибудь напишет в комментариях

Позвольте мне сказать, что вы можете еще больше улучшить ситуацию, посмотрев на текущие коэффициенты на игры, и, например, когда речь идет о матче между командами с первым номером посева, вы можете посмотреть на коэффициенты ставок в Лас-Вегасе, чтобы понять, у кого больше шансов на победу, но я не буду вдаваться в подробности.

В этом видео я буду просто выбирать команду с более высоким посевом, а когда дело дойдет до четырех команд с первым номером посева, то буду выбирать случайным образом. Ладно, это все, что мне нужно сказать для вступления.

Заранее прошу прощения, что в следующей части видео я буду использовать планшет. У меня уже возникло много технических проблем с его корректной работой, поэтому я решил снять вступление таким образом. Итак, без лишних слов, вот как рассчитать вероятность идеальной турнирной сетки March Madness, используя описанную мной стратегию.

Итак, начнём:

Это моё первое видео, снятое с помощью графического планшета Creative Pen, если так можно выразиться. Я всегда хотел снимать видео в стиле Khan Academy, но о азартных играх и математике. Итак, после вступления, перейдём к вычислениям.

Вероятность победы команды с первым номером посева над командой с шестнадцатым номером посева я оцениваю в 135 из 136, потому что на данный момент было сыграно 136 таких матчей, и команда с первым номером посева выиграла 135 раз. Это вероятность победы команды с первым номером посева в любом конкретном матче, которая составляет 99,26%.

Однако...

...есть четыре разных деления, поэтому вам нужно выполнить это четыре раза, так что возведите это в четвертую степень.

Кроме того, есть четыре разных матча , где команда под номером 2 играет против команды под номером 15. Из 136 таких случаев команда под номером 2 побеждала 127 раз. Вероятность, опять же, исходя из исторических данных, победы команды под номером 2 над командой под номером 15 составляет 93,38%, и это нужно сделать четыре раза для четырех разных дивизионов.

Аналогично, вероятность того, что игрок под номером 3 победит игрока под номером 14, составляет 115, деленное на 136, и это нужно повторить четыре раза. Затем вероятность того, что игрок под номером 4 победит игрока под номером 13, составляет 108, деленное на 136, и снова возведите это в четвертую степень для четырех игр, которые нужно выиграть.

Вероятность победы теннисиста под номером 5 над теннисистом под номером 12 составляет 89 из 136, что примерно равно 65,44% в четвертой степени. Вероятность победы теннисиста под номером 6 над теннисистом под номером 11 составляет 85 из 136, что для любой данной игры равно 62,5%. Вероятность победы теннисиста под номером 7 над теннисистом под номером 10 составляет 83 из 136. Вероятность победы в каждой игре составляет 61,03%. Наконец, вероятность победы теннисиста под номером 8 над теннисистом под номером 9 составляет 71 из 136, и опять же, это нужно повторить четыре раза.

Если вы выиграете все эти игры...

...вы пройдете первый раунд. Затем, во втором раунде, вам предстоит сыграть между командами, посеянными под первым номером, и командами, посеянными под восьмым номером. Это происходило уже 72 раза, и из этих 72 раз команда под первым номером обыграла команду под восьмым номером 58 раз. Вероятность того, что команда под первым номером обыграет команду под восьмым номером, составляет 80,56%, и вам все равно придется повторить это четыре раза.

Затем команды с 4-м номером посева сыграют с командами с 5-м номером посева. Это случалось уже 73 раза, и 41 раз побеждала команда с 4-м номером посева, что составляет вероятность в каждой игре 56,16%. А у нас еще четыре дивизиона, так что возведем это в четвертую степень.

Затем 3-я команда сыграет с 6-й. 3-я команда выиграла 41 раз из 70, вероятность победы составляет 58,57% в каждой игре. Наконец, чтобы пройти второй раунд, 2-я команда сыграет с 7-й. 2-я команда выиграла 56 раз, и это произошло 79 раз, вероятность победы в каждом случае составляет 70,89%. Хорошо, предположим, вы выиграете все эти игры, тогда вы переходите в третий раунд, где 1-я команда сыграет с 4-й.

Это случалось 61 раз за всю историю турнира , и 44 раза побеждал первый номер посева, что составляет вероятность 72,13% в каждом случае. Затем второй номер посева сыграет с третьим номером посева. Это случалось 52 раза, и в 32 из этих случаев побеждал второй номер посева. Опять же, это должно произойти еще четыре раза.

Предположим, вы выиграете все эти игры:

Тогда у вас останутся только команды с 1-м и 2-м номерами посева. Вероятность победы команды с 1-м номером посева над командой со 2-м номером посева составляет 35 из 64, опять же, на основе исторических игр, и это должно произойти четыре раза для четырех дивизионов.

Итак, если вы дошли до этого момента... то вы выиграете все четыре дивизиона , и ваша команда будет на первом месте каждый раз. Вот здесь вы начинаете выбирать случайным образом. Вам нужно еще три игры, чтобы определить лучшую из четырех команд, и, как я сказал во введении, вы просто выбираете случайным образом, поэтому ваши шансы на победу каждый раз будут 1 к 2, и вам нужно еще три игры.

Это ваша вероятность выигрыша, используя мою стратегию , и она составляет 1 к 42 743 890 552. Вот и всё. Я считаю, что это наиболее точная цифра для заполнения идеальной турнирной сетки March Madness.

Как я уже говорил во введении, вы можете улучшить свой результат, посмотрев на текущие коэффициенты на рынке ставок. Спасибо за просмотр этого видео. Я знаю, что оно получилось не очень хорошим.

Рассматривайте это как полезный опыт для меня, и, повторюсь, всё это изложено в письменном виде на моём сайте wizardofodds.com в разделе ставок на спорт, а затем найдите страницу о том, как составить идеальную турнирную сетку March Madness. Думаю, больше нечего добавить.

Спасибо за просмотр.

Автор: Michael Shackleford