Сик Бо - Рассчитайте шансы и выиграйте | Видео

Привет всем, это Майк.

Вы узнаете, как рассчитать шансы в игре Сик Бо . Вкратце, Сик Бо — это очень древняя китайская игра, основанная на бросании трех игральных костей. В игре существует множество вариантов ставок.

Что я собираюсь сделать :

Я разделю эту тему на два видео, потому что все на моём форуме жалуются, что мои видео слишком длинные. В первой части я объясню, как рассчитать вероятность выпадения любой суммы от 3 до 18 на трёх игральных костях, а также вероятность выпадения 0, 1, 2 или 3 на любой грани кости.

Как только мы получим ответы на эти вопросы…

…мы можем перейти ко второй части и проанализировать, какую выгоду вы получаете от всех различных ставок в сик бо.

Давайте ответим на вопрос : «Какова вероятность выпадения любой заданной суммы при броске трех шестигранных кубиков?» Метод, который я вам сейчас покажу, будет работать для любого количества кубиков.

Хочу выразить благодарность Роберту Гудханду из Сомерсета, Великобритания, за этот хитрый прием. Он описан в моей рубрике «Спроси волшебника» (№ 264). Сейчас я поделюсь им с вами.

Для начала нам нужно определить пять фиктивных клеток. Вы поймете почему через минуту. Теперь я перечислю все суммы от 1 до 18. Очевидно, что на одном кубике есть только один способ выбросить 1, 2 или 6.

У каждой грани есть одна сторона, так что это довольно очевидно. При игре с двумя кубиками нужно сложить значения в левом столбце, в данном случае, в столбце B, начиная с одной ячейки слева и заканчивая пятью ячейками выше.

В данном случае…

…Я работаю с ячейкой C8. Она показывает количество способов получить в сумме два броска двух кубиков. Я суммирую значения в ячейках B2–B7. Если ячейка пустая, Excel правильно считает, что в ней ноль.

Я просто копирую и вставляю это вниз, пропуская все возможные суммы до 12. Вы увидите, что при сумме двух есть один способ бросить. При сумме трех есть два способа. При сумме четырех есть три способа.

Итак, почему это работает?

Рассмотрим сумму двух. Чтобы получить два, на первом кубике должна выпасть единица, а на втором — единица. Есть только один способ , как на первом кубике может выпасть единица, и, очевидно, только один способ, как на втором кубике может выпасть единица. Чтобы получить три, есть два способа.

Есть один способ, которым на первом кубике может выпасть единица, а на втором — двойка , плюс один способ, которым на первом кубике может выпасть двойка, а на втором — единица. В сумме это четыре способа, при которых на первом кубике должно выпасть от единицы до тройки.

Всего пять...

Сумма результатов первого кубика должна составлять от одного до четырех. Пока результат первого кубика находится в этом допустимом диапазоне, есть один способ, которым следующий кубик может дать желаемую сумму.

Перейдём к трём игральным костям.

Это абсолютно тот же самый метод. Мы можем просто скопировать и вставить ту же формулу. Я могу взять её из любого места в диапазоне, который мы только что рассмотрели. Я просто сделаю это здесь, скопирую и вставлю её на одну ячейку правее, а затем скопирую и вставлю вниз. Там у нас есть количество комбинаций для любой суммы от 3 до 18 при игре на трёх кубиках.

Например:

Есть один способ получить в сумме три, три способа получить в сумме четыре, шесть способов получить в сумме пять и так далее. Почему это работает? — можете спросить вы снова. Что ж, давайте рассмотрим, например, сумму семь. Чтобы получить в сумме семь с помощью трех кубиков, это можно сделать, если сумма с помощью двух кубиков равна двум, а затем к ней добавить пятерку.

Есть один способ, которым первые две игральные кости могут дать двойку. Другой способ — если сумма первых двух костей равна трём, а третья — четвёрке. Как мы только что видели, есть два способа, которыми сумма первых двух костей может дать три, и три способа, которыми сумма первых двух костей может дать четыре.

Чтобы получить в общей сложности семь …

…сумма ваших первых двух кубиков должна составлять от двух до шести. Мы только что видели, что общее количество возможных вариантов равно сумме чисел от одного до пяти, то есть 15. Давайте составим удобную таблицу. И снова, вот ваша сумма.

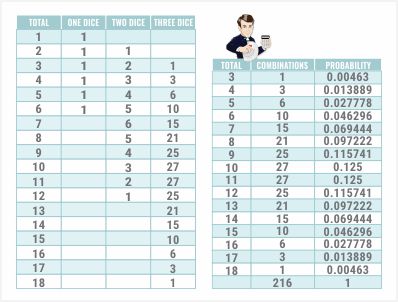
Вот возможные комбинации :

Давайте возьмём сумму этих чисел, 216. Это число кажется знакомым. Возможно, это шесть в третьей степени.

Наконец, давайте найдем вероятность каждой суммы:

Мы просто берем количество комбинаций, деленное на сумму. Это вероятность выпадения любой заданной суммы от 30 до 18. Далее рассмотрим вероятность выпадения любой конкретной грани игральной кости от нуля до трех раз. В сик бо шесть различных ставок, по одной на каждую грань кости.

Игрок выигрывает со счетом один к одному, если выбранная грань выпала один раз, два к одному, если она выпала два раза, и три к одному, если она выпала три раза. Однако многие ошибочно складывают вероятности, когда говорят о нескольких событиях, и каждая игральная кость рассматривается как независимое событие.

Мы не складываем, мы умножаем.

Мне нравится сначала размышлять о комбинациях. Допустим, вы просто выбрали шестерку. Каково, точнее, количество комбинаций, в которых шестерка может выпасть все три раза на трех кубиках? На самом деле, всего одна. Есть только один способ, как это может произойти: 6-6-6. А как насчет двух раз?

Например:

6-6-4 или 2-6-6, 6-1-6. Две из игральных костей выпадают шестеркой, а одна — чем-то другим. Это «что-то другое» может быть любой из пяти других граней, и это «что-то другое» может выпадать на любой из трех игральных костей. Общее количество способов, которыми выбранная вами грань может выпасть дважды из трех игральных костей, равно 15.

А сколько существует способов, которыми это слово может появиться хотя бы один раз?

Итак, две другие игральные кости, которые не являются выбранной вами гранью, могут иметь любую из пяти возможных граней. Мы умножаем 5 на 5, потому что одна из них может иметь любую грань, кроме шестерки или любой другой выбранной вами, а другая также может иметь любую из пяти других граней.

Окончательно…

…мы умножаем на три, потому что выбранная вами грань может совпадать с любой из трех других граней. Количество способов бросить выбранную вами грань за один раз равно 5 x 5 x 3, что равно 75. Например, если вы выбрали грань шесть, это может быть 6-1-2, 1-4-6, 1-6-5, 2-6-2, 6-1-3 и так далее.

А как насчет количества комбинаций, когда ни одна из выбранных вами граней кубика не выпадает?

Итак, каждая из трёх игральных костей может представлять собой одно из пяти значений. Пять игральных костей — то есть три игральные кости, пять различных комбинаций для каждой, кроме выбранной вами грани, — это 5 x 5 x 5 комбинаций, или 125. Давайте возьмём сумму всех этих комбинаций, и мы снова получим 216. Опять же, это шесть в третьей степени, так что я, должно быть, сделал что-то правильно.

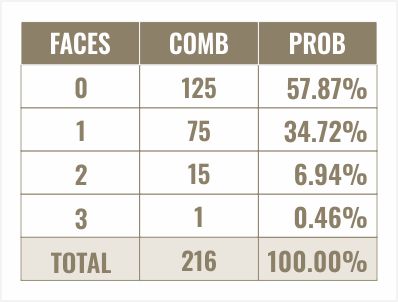
Наконец, давайте рассмотрим вероятность.

Мы просто берем количество комбинаций и делим его на общее количество комбинаций. Запишем это в процентах. Здесь мы видим, что вероятность выпадения выбранного вами символа «ноль» составляет 57,87%, один раз — 34,72%, два раза — 6,94%, и три раза — 0,46%.

Надеюсь, это было понятно. Надеюсь увидеть вас во второй части, где я рассчитаю коэффициенты множества различных ставок на сик бо.

Спасибо за просмотр.

Этот документ создан с помощью инструментов мгновенного редактирования HTML. Нажмите здесь и протестируйте его бесплатно.

Часть 2

Автор: Michael Shackleford