WOO logo

Wizard рекомендует

Спросите Волшебника #171

Я не покупаю вашу игру NIM ! Я всегда думал, что ключ к победе — это оставить противнику (в данном случае, компьютеру) точки, сумма которых равна следующему наименьшему числу, равному его двоичной сумме, то есть, если у меня 17 точек, я забираю 2 и оставляю 15, сумму двоичных чисел 1, 2, 4, 8. Но это, похоже, не работает. Я прав или нет?

Jack от Troy

Вы на верном пути с двоичными числами, но это не совсем выигрышная стратегия. Во-первых, если вы можете оставить противнику нечётное количество строк по одному числу в каждой, сделайте это. В противном случае разбейте каждую строку на её двоичные компоненты. Например, 99 будет 64+32+2+1. Затем сложите количество каждого компонента по всем строкам. Затем найдите ход, который оставит противнику чётное количество всех двоичных компонентов по всем строкам.

Рассмотрим пример. Предположим, настала ваша очередь, и ситуация выглядит следующим образом.

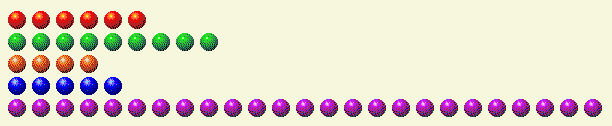
В следующей таблице каждая строка разбита на двоичные компоненты.

Ход игрока 1

Ряд 1 2 4 8 16
6 0 1 1 0 0
9 1 0 0 1 0
4 0 0 1 0 0
5 1 0 1 0 0
25 1 0 0 1 1
Общий 3 1 3 2 1

Как видите, количество единиц, двоек, четверок и шестнадцаток нечетное. Очевидно, нам нужно уменьшить число 25 в ряду до 16, чтобы исключить 16-ю единицу. Чтобы сумма двоичных компонентов оставалась четной, нам нужно убрать 1, добавить 2, добавить 4, оставить 8 и убрать 16. Это означает, что лучший ход — 2+4+8=14 в последнем ряду. Оставив 14 в нижнем ряду, мы получаем следующее.

Первый ход компьютера

Ряд 1 2 4 8 16
6 0 1 1 0 0
9 1 0 0 1 0
4 0 0 1 0 0
5 1 0 1 0 0
14 0 1 1 1 0
Общий 2 2 4 2 0

Затем очередь переходит к компьютеру, и в итоге мы получаем вот это.

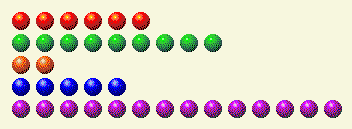
Вот бинарное разложение этого понятия.

Ход игрока 2

Ряд 1 2 4 8 16
6 0 1 1 0 0
9 1 0 0 1 0
2 0 1 0 0 0
5 1 0 1 0 0
14 0 1 1 1 0
Общий 2 3 3 2 0

Здесь нам нужно убрать 2 и 4, чтобы получить равные суммы. Есть только одна строка, 14, в которой присутствуют оба компонента. Поэтому уберем из нее 6, останется 8.

Второй ход компьютера

Ряд 1 2 4 8 16
6 0 1 1 0 0
9 1 0 0 1 0
2 0 1 0 0 0
5 1 0 1 0 0
8 0 0 0 1 0
Общий 2 2 2 2 0

Затем очередь переходит к компьютеру, и в итоге мы получаем вот это.

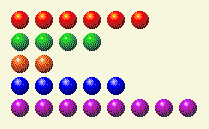
Теперь нам нужно поменять местами столбцы 1, 4 и 8.

Ход игрока 3

Ряд 1 2 4 8 16
6 0 1 1 0 0
4 0 0 1 0 0
2 0 1 0 0 0
5 1 0 1 0 0
8 0 0 0 1 0
Общий 1 2 3 1 0

Это можно сделать, изменив строку с 8 на 5 следующим образом.

Третий ход компьютера

Ряд 1 2 4 8 16
6 0 1 1 0 0
4 0 0 1 0 0
2 0 1 0 0 0
5 1 0 1 0 0
5 1 0 1 0 0
Общий 2 2 4 0 0

Затем очередь переходит к компьютеру, и в итоге мы получаем вот это.

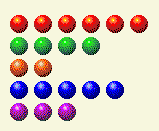
Теперь нам нужно поменять местами суммы 2 и 4.

Ход игрока 4

Ряд 1 2 4 8 16
6 0 1 1 0 0
4 0 0 1 0 0
2 0 1 0 0 0
5 1 0 1 0 0
3 1 1 0 0 0
Общий 2 3 3 0 0

Это можно сделать, заменив 6 на 0.

Четвёртый ход компьютера

Ряд 1 2 4 8 16
0 0 0 0 0 0
4 0 0 1 0 0
2 0 1 0 0 0
5 1 0 1 0 0
3 1 1 0 0 0
Общий 2 2 2 0 0

Затем очередь переходит к компьютеру, и в итоге мы получаем вот это.

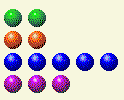
Теперь нам нужно поменять местами двойки и четверки.

Ход игрока 5

Ряд 1 2 4 8 16
0 0 0 0 0 0
2 0 1 0 0 0
2 0 1 0 0 0
5 1 0 1 0 0
3 1 1 0 0 0
Общий 2 3 1 0 0

Этого можно добиться, изменив ряд из 5 чисел на 3. Если вам удастся привести противника к ситуации x, x, y, y, вы обязательно выиграете, если сможете поддерживать эту ситуацию до конца.

Поворот компьютера 5

Ряд 1 2 4 8 16
0 0 0 0 0 0
2 0 1 0 0 0
2 0 1 0 0 0
3 1 1 0 0 0
3 1 1 0 0 0
Общий 2 4 0 0 0

В следующих нескольких ходах я заставляю компьютер использовать последовательность x, x, y, y. В этот раз компьютер оставляет мне 2, 2, 3, 2; поэтому я оставляю ему 2, 2, 2, 2.

Затем компьютер выдает мне 2,2,1,2. Я оставляю ему 2,2,1,1.

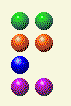
Компьютер оставляет мне 2, 2, 1. Я оставляю ему 2, 2. Если вам удастся выстроить два одинаковых ряда против вашего противника, вы обязательно выиграете, главное — чтобы ряды были одинаковыми.

Затем компьютер оставляет мне одну кучу из 2 штук, и я убираю 1.

Игра подошла к концу.

Я понимаю, что ставка «пут» — хорошая ставка, когда коэффициенты 10x или больше. То есть, если выпадает 6 или 8, ставьте, например, 5 долларов плюс 50 долларов бесплатных коэффициентов. Мой вопрос: зачем ждать выпадения очка? Почему бы не поставить на линию «пас», а затем, если выпадет 6 или 8, поставить все 10-кратные коэффициенты? Таким образом, вы получаете преимущество коэффициентов, плюс преимущество от первого броска 7/11. Я что-то упускаю?

Jay от Whitestone

Согласен. Я не рекомендую делать ставки на «пут» или «плейс», потому что, как вы сказали, шансы выше, если делать ставку на линию, а затем ставку на максимальные шансы. Однако некоторым людям абсолютно необходимо делать ставки непосредственно на очки. Если это так, я рекомендую делать лучшую ставку между «плейс», «бай» и «пут», что я более подробно объясняю в разделе, посвященном крэпсу.
Мы с другом играли в Лас-Вегасе. У нас разгорелся большой спор о том, что статистически имеет лучшие шансы: удвоить ставку, если у игрока 10 очков, а у дилера 7, или удвоить ставку, если у игрока 11 очков, а у дилера 10, в игре с двумя колодами. Мне показалось, что лучше первый вариант.

Brett от Alhambra

Приложение 9 к блэкджеку было создано именно для таких вопросов. Предполагая наличие 6 колод, моя таблица показывает, что ожидаемая выгода от удвоения 8+2 против 7 составляет 0,396342. Ожидаемая выгода от удвоения 8+3 против 10 составляет 0,176919. Так что вы правы, 10 против 7 — гораздо более выгодная комбинация.
Ваш сайт потрясающий, я многому на нём научился. На флопе в холдеме у вас 20 карт, которые дают вам выигрышную комбинацию. Почему процент составления выигрышной комбинации к риверу составляет 67,5%, а не 86% (20/47 + 20/46)? Я везде искал, но так и не смог разобраться, хотя понимаю, что это, вероятно, очень элементарно. Буду благодарен за помощь, спасибо!

Kevin от Vernon, NJ

Спасибо! Ваш способ предполагает двойной подсчет получения двух из 20 необходимых карт. Вероятность получения одной из 20 необходимых карт на терне составляет 20/47 = 0,4255. Вероятность того, что вы не получите ее на терне, но получите на ривере, составляет (27/47)*(20/46) = 0,2498. Таким образом, общая вероятность составляет 0,4255 + 0,2498 = 0,6753.

Недавно я стал свидетелем ситуации в местном племенном казино, связанной с протоколом игры в крэпс, которая меня озадачила, и я хотел бы узнать, пожалуйста, подробности. При первом броске игрок «А» выбросил число и установил точку. Для следующего броска игрок рядом с «А» (игрок «Б») взял кости и бросил их. Неясно, почему он это сделал, и знал ли он вообще «А». Один из других игроков возразил, указав, что «Б» не был тем, кто бросил кости изначально. После долгих обсуждений и недоумения дилеров и кассира кости были переданы следующему игроку (игроку «С»), который и завершил раздачу (в итоге он выбил семерку).

Был ли это правильный протокол в данной ситуации, и если да, то какова его логика? Если игрок «А» по какой-то причине просто не хотел больше бросать кубики, почему ему не следовало разрешить отдать кубики? Если игрок «Б» взял кубики, потому что не понимал правил игры, или если человечек по ошибке положил их перед ним, разве кубики не должны были вернуться к «А», чтобы завершить раздачу?

DAVID от BAINBRIDGE ISLAND, WA

Я задал этот вопрос «Человеку из костей» на сайте nextshooter.com . Вот что он ответил.

Если игрок, не являющийся правильным бросающим, берет кубики и бросает их, это должно считаться «нет результата, нет броска», и кубики должны быть возвращены правильному бросающему. Хотя это действительно правильное правило, в некоторых случаях боксмен может разрешить бросок, если результат благоприятен для всех или большинства игроков. В некоторых случаях результат броска может не повлиять на ставки ни одного из игроков. Также... Любой игрок может попросить отправить кубики следующему бросающему для завершения раздачи. В таких случаях могут быть отправлены те же самые кубики, или новый бросающий может запросить новые кубики. После завершения броска ТОТ ЖЕ бросающий может затем бросить СВОЮ СОБСТВЕННУЮ руку, таким образом, имея более одной руки.

Какова вероятность получить сумму больше 100 при броске 20 игральных костей? С уважением.

Terje от Stockholm

Я начал использовать нормальное приближение для решения этой задачи, но вероятность получения более 100 точек слишком низка, чтобы этот метод был точным. Поэтому я провел случайное моделирование 8,25 миллионов испытаний, и количество испытаний, в которых было 101 точка или больше, составило 127. Таким образом, вероятность составляет примерно 1 к 65 000.
Время для еще одного вопроса из «Сделки или нет». Допустим, после всех сделок с банкиром и выступлений Селин Дион у вас осталось два чемодана: на 500 000 долларов и на 1 000 000 долларов. Предложение банкира, я полагаю, будет чуть меньше 750 000 долларов. Какой бы вы выбрали? А если бы остались два чемодана на 0,01 доллара и на 1 000 000 долларов? Думаю, все дело в том, азартный вы человек или нет, и это никак не связано с вероятностями. Причина, по которой я спрашиваю, заключается в том, интересно, выиграет ли КТО-НИБУДЬ когда-нибудь 1 000 000 долларов (даже если он выбрал волшебный чемодан).

Jason от Vancouver

Когда призы становятся суммами, меняющими жизнь, мудрый игрок должен играть консервативно, стремясь к максимизации ожидаемой выгоды. Хорошая стратегия должна заключаться в максимизации ожидаемого счастья. Хорошей функцией для измерения счастья, на мой взгляд, является логарифм вашего общего богатства. Возьмем человека с уже имеющимся состоянием в 100 000 долларов, которому предлагаются два варианта: 0,01 доллара и 1 000 000 долларов. При выборе варианта «нет сделки» ожидаемое счастье составляет 0,5 * log(100 000,01 доллара) + 0,5 * log(1 100 000 долларов) = 5,520696. Пусть b — банковское предложение, в отношении которого игрок безразличен.

log(b) = 5,520696
b = 10 5.520696
b = 331 662,50 долл. США.

Таким образом, этот гипотетический игрок должен быть равнодушен к предложению банка в размере 331 662,50 долларов. Чем меньше у вас денег в начале игры, тем консервативнее вы должны играть. Обычно на поздних этапах игры предложения банка близки к ожидаемой сумме, иногда немного превышают её. Единственный рациональный случай, когда игрок может выиграть миллион, — это если у него было много денег в начале игры и/или предложения банка были необычайно скупыми. Похоже, продюсерам нравятся трудолюбивые люди из среднего класса, поэтому мы вряд ли увидим кого-то, кто может позволить себе быть легкомысленным, когда речь идёт о больших суммах. Я также никогда не видел, чтобы банк предлагал менее 90% от ожидаемой суммы на поздних этапах игры. Время, когда мы увидим, как кто-то выиграет миллион, — это когда на шоу появится заядлый игрок, который не может остановиться. Когда это произойдёт, я буду болеть за банкира.

Мне очень нравится ваш сайт! Я только что наткнулся на ваш подробный список столов для блэкджека в Лас-Вегасе и их преимуществ, поэтому мне стало интересно: предположим, есть два стола для блэкджека, один с преимуществом 0,2% и минимальным взносом в 10 долларов, а другой — 0,4% и минимальным взносом в 5 долларов. Оба стола имеют одинаковый проигрыш в 0,02 доллара за раздачу. Есть ли какое-либо преимущество в выборе одного стола перед другим?

Milton от Santa Fe

Спасибо. Чтобы ответить на этот вопрос, сначала нужно спросить себя, зачем вы вообще играете в азартные игры. Если вы пытаетесь проиграть как можно меньше, то вам вообще не следует играть. Однако, если вы играете ради удовольствия, то я бы выбрал игру на 10 долларов с преимуществом в 0,2%. Ожидаемый убыток будет таким же, но вы получите большую прибыль, делая более крупные ставки.
В казино Niagara есть дополнительная ставка в Пай Гоу Покер, которая выплачивается из джекпота, а не по фиксированным коэффициентам. Мне интересно, какой должна быть сумма джекпота, чтобы эта ставка окупилась (при условии, что раздача составлена таким образом, чтобы максимизировать отдачу от ставки на джекпот).

William от Mississauga, Ontario

Точка безубыточности составляет 102 680,24 доллара. Я только что добавил анализ этой ставки в свой раздел о дополнительных ставках в Пай Гоу Покер .
Я мало что знаю о покере, но мне он нравится, так что, может быть, вы сможете мне кое-что прояснить. Во время недавней поездки в Вегас с женой мы остановились в отеле Arizona Charlie's Decatur. Причиной нашего выбора стало то, что на их сайте рекламировался Холдем с бай-ином $2-$4. В первое утро мы спустились в покер-зал и записались на игру с бай-ином $2-$4. Я заметил, что покерный парень записывает наши имена в столбцы с бай-ином $4-$8. Поэтому я сказал ему, что мы хотим $2-$4 (на том же листе был столбец с надписью «$2-$4»). Он объяснил, что $2-$4 это: $2 до флопа, $4 после флопа и $8 после терна и ривера. Я объяснил ему, что имею в виду под $2-$4: $2 до и после флопа и $4 после терна и ривера. Он рассмеялся, как будто мы не понимаем, о чем говорим, и сказал, что так игра не ведется. В итоге мы провели остаток поездки, играя в покер в Gold Coast. Нормальны ли такие ставки для покерных клубов? (В итоге я сказал управляющему покерного клуба, что если бы мы могли позволить себе играть в Холдем со ставками $4-$8, мы бы не остановились в Arizona Charlie's.)

Mike от Philadelphia, PA

Я согласен, что игра "2/4" означает, что ставки составляют 2 доллара до терна и 4 доллара после терна. Однако малый блайнд, скорее всего, равен 1 доллару. Похоже, когда в Arizona Charlie's называют игру "2/4", они имеют в виду блайнды, что означает малый блайнд в 2 доллара и большой блайнд в 4 доллара, что подразумевает ставки в 8 долларов после терна. Я никогда раньше не слышал такого использования, поэтому не виню вас за удивление.

P.S. Позже я получил следующее от Энтони, управляющего покерным залом.

Я являюсь супервайзером покер-рума. Я просто хотел сообщить вам о правильной формулировке лимитов в покере Техасский Холдем. Если игра обозначена как $2/4, это относится к ставкам. (Игра обозначается блайндами только в безлимитном формате.) $2 на префлопе и постфлопе, $4 на терне и ривере. Игра, обозначенная как $2/$4/$8 (что, как я подозреваю, и имел в виду предыдущий автор письма), означает $2 на префлопе, $4 на постфлопе, $8 на терне и ривере. Также возможно обозначение игры как $2/$4/$6/$8. Просто передаю информацию, хорошие супервайзеры покер-румов хотят, чтобы у людей было как можно больше информации.