Спросите Волшебника #253
Я не понимаю, как так получается, что в ваших таблицах силы карт Техасского Холдема A-7 занимает более низкое место, чем KJ одномастные, но на вашем калькуляторе у A7 выше вероятность выигрыша.
Хороший вопрос. Для удобства других читателей, вот шансы против случайной руки с каждой из этих двух стартовых рук в игре для двух игроков:
KJ Suited против A-7 Off-Suit
| Рука | Победить | Терять | Рисовать | Ожидаемое значение |
К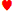 Дж. Дж.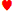 | 0.6148 | 0.3634 | 0,0218 | 0,2513 |
А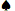 7 7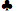 | 0.5717 | 0.3949 | 0,0334 | 0.1768 |
Однако, согласно моему калькулятору для игры в Техасский Холдем вдвоем, вероятность того, что эти две руки окажутся друг напротив друга, такова:
Победы A7 = 53,52%
Победы К.Дж.: 46,10%
Ничья = 0,39%
Таким образом, KJ в одномастных картах занимает более высокое место в моей таблице, но уступает A7 в прямом сравнении. Почему?
Ответ сложно объяснить. При сравнении двух рук необходимо учитывать их взаимодействие. Например, в таблице силы стартовых рук AK разномастная лишь немного лучше, чем AQ разномастная, с ожидаемыми значениями 0,3064 и 0,2886 соответственно. Однако, если сравнить их, AK значительно превосходит AQ, как показано ниже:
Победы АК = 71,72%
Победы AQ = 23,69%
Ничья = 4,58%
В разномастных тузах и валетах против одномастных королей и валетов туз значительно превосходит короля и валета. Наибольшие шансы на победу у игрока с королем и валетом возникают, если у него пара королей или валетов, и тузов не выпадает. Я показываю, что вероятность этого составляет всего 37,73%. Остальные 46,10% вероятности победы игрока с королем и валетом приходятся на более сильные руки.
Хотя A7 сильна против KJ, она чаще оказывается под контролем случайных рук, чем KJ.
Возможно, это неудачное сравнение, но это чем-то похоже на игру «камень-ножницы-бумага» . Среди опытных игроков каждый бросок должен иметь примерно одинаковый показатель силы. Однако, если один игрок бросает бумагу, а другой — ножницы, показатели силы ничего не значат, и ножницы выиграют.
В казино Bighorn and Longhorn в Лас-Вегасе разрешено удваивать ставку на три карты в блэкджеке. Следует ли мне внести какие-либо изменения в свою стратегию, исходя из этого правила?
Один из читателей моего сайта Wizard of Vegas предлагает внести следующие изменения по сравнению со стандартной стратегией игры с несколькими колодами, где дилер берет карту, если у него «мягкая» 17:
- Мягкий удар 13 против 5 или 6
- Удар по 2 картам, мягкий 15 против 4
- Удар 3,3 против 2
Причина, по которой стоит брать дополнительные карты с мягкими руками, заключается в том, что после взятия карты вы можете получить более выгодный вариант удвоения с мягкими руками. Ценность взятия карт с тремя картами выше по этому правилу, потому что получение туза будет хорошим вариантом удвоения с тремя картами.
Этот вопрос был поднят и обсужден на форуме моего дочернего сайта Wizard of Vegas .
Если монету подбросить 100 раз, какова вероятность того, что хотя бы раз подряд выпадет не менее 7 орлов?
Если существует простое, нерекурсивное выражение для ответа, мне о нём неизвестно. Однако существует простое рекурсивное выражение для ответа.
f(n) = pr(решка при первом броске)×f(n-1) +
pr(орёл при первом броске, решка при втором броске)×f(n-2) +
pr(орёл в первых двух бросках, решка в третьем броске)×f(n-3) +
pr(орёл в первых трёх бросках, решка в третьем броске)×f(n-4) +
pr(орёл в первых 4 бросках, решка в четвёртом броске)×f(n-5) +
pr(орёл в первых 5 бросках, решка в пятом броске)×f(n-6) +
pr(орёл в первых 6 бросках, решка в шестом броске)×f(n-7) +
pr(орёл в первых 7 бросках) =
(1/2)×f(n-1) +
(1/2) 2 ×f(n-2) +
(1/2) 3 ×f(n-3) +
(1/2) 4 ×f(n-4) +
(1/2) 5 ×f(n-5) +
(1/2) 6 ×f(n-6) +
(1/2) 7 ×f(n-7) +
(1/2) 7
Где:
f(n) = вероятность успеха при n бросках.
pr(x) = вероятность наступления события x.
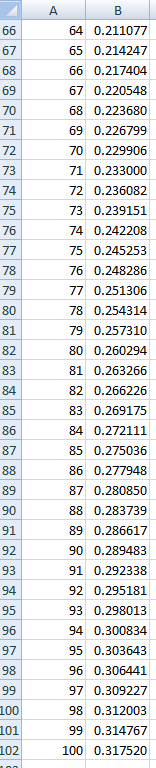
Электронные таблицы идеально подходят для решения подобных задач. На скриншотах таблицы ниже я указал вероятность 0 для ячеек B2–B8, потому что невозможно получить 7 орлов подряд за 6 или менее бросков. Для ячейки B9 я ввел формулу:
=(1/2)*B8+(1/2)^2*B7+(1/2)^3*B6+(1/2)^4*B5+(1/2)^5*B4+(1/2)^6*B3+(1/2)^7*B2+(1/2)^7
Затем я скопировал и вставил это из ячейки B10 в ячейку B102, что соответствует 100 броскам. Вероятность составляет 0,317520. Случайное моделирование это подтверждает.
 |  |
После первоначальной публикации Рик Перси поделился со мной своим решением задачи матричной алгебры. Вот оно, изложенное моими собственными словами. Я предполагаю, что читатель уже знаком с основами матричной алгебры.
Во-первых, в любой момент времени ласт может находиться в восьми различных состояниях:
p 1 = Вероятность успеха при условии, что вам нужно еще 7 орлов с текущей точки.
p 2 = Вероятность успеха при условии, что вам нужно еще 6 орлов с текущей точки.
p 3 = Вероятность успеха при условии, что вам нужно еще 5 орлов с текущей точки.
p 4 = Вероятность успеха при условии, что вам нужно еще 4 орла с текущей точки.
p 5 = Вероятность успеха при условии, что вам нужно еще 3 орла с текущей точки.
p 6 = Вероятность успеха при условии, что вам нужно еще 2 орла с текущей точки.
p 7 = Вероятность успеха при условии, что вам нужно еще 1 орёл с текущей точки.
p 8 = Вероятность успеха при условии, что вам больше не нужно выпадать орлом = 1.
Определим макстрикс S n как вероятность нахождения в каждом состоянии после n -го броска. S 0 представляет собой вероятности до первого броска, когда существует 100% вероятность нахождения в состоянии 0. Таким образом, S 0 =
| 1 0 0 0 0 0 0 0 |
Пусть T — матрица преобразования двух последовательных переворотов, или S n в S n+1 , где S n+1 = T × S n
- Если вы находитесь в состоянии 1, то после одного броска у вас есть 0,5 шанса оказаться в состоянии 2 (при выпадении орла) и 0,5 шанса остаться в состоянии 1 (при выпадении решки).
- Если вы находитесь во втором состоянии, то после одного броска у вас есть 0,5 шанса оказаться в третьем состоянии (при выпадении орла) и 0,5 шанса вернуться в первое состояние (при выпадении решки).
- Если вы находитесь в состоянии 3, то после одного броска у вас есть 0,5 шанса оказаться в состоянии 4 (при выпадении орла) и 0,5 шанса вернуться в состояние 1 (при выпадении решки).
- Если вы находитесь в состоянии 4, то после одного броска у вас есть 0,5 шанса оказаться в состоянии 5 (при выпадении орла) и 0,5 шанса вернуться в состояние 1 (при выпадении решки).
- Если вы находитесь в состоянии 5, то после одного броска у вас есть 0,5 шанса оказаться в состоянии 6 (при выпадении орла) и 0,5 шанса вернуться в состояние 1 (при выпадении решки).
- Если вы находитесь в состоянии 6, то после одного броска у вас есть 0,5 шанса оказаться в состоянии 7 (при выпадении орла) и 0,5 шанса вернуться в состояние 1 (при выпадении решки).
- Если вы находитесь в 7-м состоянии, то после одного броска у вас есть 0,5 шанса оказаться в 8-м состоянии (при выпадении орла) и 0,5 шанса вернуться в 1-е состояние (при выпадении решки).
- Если вы находитесь в состоянии 8, значит, вы добились успеха и останетесь в состоянии 8 с вероятностью 1,0.
Представим все это в виде матрицы перехода T =
| 0.5 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.5 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.5 0.0 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.5 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.5 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.5 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.5 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.5 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 |
Чтобы определить вероятность каждого состояния после одного броска...
(1) S 1 = S 0 × T
А что, если после двух переворотов?
(2) S 2 = S 1 × T
Подставим уравнение (1) в уравнение (2)...
(3) S 2 = S 0 × T × T = S 0 × T 2
А что будет после 3 переворотов?
(4) S 3 = S 2 × T
Подставляя уравнение (3) в (4)...
(5) S 3 = S 0 × T 2 × T = S 0 × T 3
Мы можем продолжать это делать вплоть до штата и после сотой попытки переворота...
S 100 = S 0 × T 100
Итак, что же такое T 100 ? До появления компьютеров, должно быть, было очень сложно разобраться в таких вещах. Однако, с помощью функции MMULT в Excel и множества операций копирования и вставки, мы получаем T 100 =
| 0.342616 0.171999 0.086347 0.043347 0.021761 0.010924 0.005484 0.317520 |
| 0.339863 0.170617 0.085653 0.042999 0.021586 0.010837 0.005440 0.323005 |
| 0.334379 0.167864 0.084271 0.042305 0.021238 0.010662 0.005352 0.333929 |
| 0.323454 0.162380 0.081517 0.040923 0.020544 0.010313 0.005178 0.355690 |
| 0.301693 0.151455 0.076033 0.038170 0.019162 0.009620 0.004829 0.399038 |
| 0.258346 0.129694 0.065109 0.032686 0.016409 0.008237 0.004135 0.485384 |
| 0.171999 0.086347 0.043347 0.021761 0.010924 0.005484 0.002753 0.657384 |
| 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 1.000000 |
Термин в правом верхнем углу показывает вероятность нахождения в состоянии 8 после 100 бросков, которая составляет 0,317520.
Недавно в казино Tuscany прошла акция, в рамках которой за 30 дней, набрав 30 блэкджеков, можно было выиграть бонус в размере 100 долларов. Изначально минимальная ставка для получения штампа на карту составляла 5 долларов. Однако позже я узнал, что минимальная ставка была повышена до 15 долларов. Я написал жалобу менеджеру казино, в которой, в частности, указал:
Я просто хотел выразить своё разочарование по поводу этого изменения, если оно действительно произошло. У меня так и не было возможности воспользоваться этой акцией, и я сомневаюсь, что смогу сделать это сейчас. Время, необходимое для получения 30 блэкджеков (мне сказали, что это около 8 часов непрерывной игры), кажется неразумным при ставке в 15 долларов за раздачу, когда акция по-прежнему предлагает только 100 долларов.
Вот ответ, который я получил:
В ответ на ваше электронное письмо по поводу акции «Blackout» в блэкджеке, я не уверен, откуда вы взяли информацию о том, сколько времени требуется для заполнения карточки «Blackout». Мы видели, как игроки заполняли карточку менее чем за четыре часа. Кроме того, у вас есть тридцать дней на заполнение карточки. Надеюсь, вы понимаете, что это вполне выполнимая задача за такое время. СПАСИБО за ваше письмо. Приятно получать отзывы от наших клиентов. Надеюсь, вы попробуете и выиграете немного денег!
Какова вероятность получить 30 блэкджеков за четыре часа?
Согласно моим сравнительным играм , игроки в блэкджек разыгрывают около 70 раздач в час. Вероятность блэкджека в игре с шестью колодами составляет 24*96/комбинация(312,2)=4,75%. Я предполагаю, что ничья в блэкджеке всё равно получает отметку. Таким образом, для заполнения колоды потребуется примерно 30/0,0475=632 раздачи, или 9,02 часа.
Вероятность заполнения карточного поля за 4 часа, при условии 280 раздач, составляет 1 к 30 000, играя по одной раздаче за раз. Я подозреваю, что любой игрок, достигший цели за четыре часа, играл как минимум по две раздачи за раз.
Этот вопрос был поднят и обсужден на форуме моего дочернего сайта Wizard of Vegas .


