Спросите Волшебника #284
Вы слышали о автосалоне в Сиэтле, которому пришлось заплатить 420 000 долларов из-за того, что «Сиэтл Сихокс» не смогли забить ни одного очка в матче против «Нью-Йорк Джайентс»? Я читал, что им пришлось заплатить 7000 долларов за страховой полис. Какова была бы справедливая страховая премия?
Согласно статье «Автосалон в Вашингтоне выплатил 420 000 долларов после победы «Сиэтл Сихокс» над «Нью-Йорк Джайентс» всухую» , автосалон проводил акцию, в рамках которой двенадцать победителей должны были получить по 35 000 долларов каждый, если «Сихокс» одержат победу над «Нью-Йорк Джайентс» в матче 15-й недели, состоявшемся 15 декабря 2013 года. В статье также говорится, что автосалон заплатил 7000 долларов за страховой полис на случай, если это действительно произойдет.
На основе анализа всех игр НФЛ с сезонов 1983 по 2012 год, в каждой конкретной игре одна из сторон оставалась без очков. Однако, учитывая, что «Джайентс» считались аутсайдерами с разницей в семь очков, а средний тотал был выше среднего, я бы предположил, что вероятность того, что они не наберут ни одного очка, была выше среднего. Тотал в той игре составлял 41. Давайте немного поразмышляем, чтобы вычислить ожидаемое количество очков, набранных «Джайентс».
Позволять:
s = очки "Сихокс"
g = очки "Гигантов"
Мы знаем, что s+g=41 и s=g+7, исходя из разницы очков и общего/меньшего количества очков.
Подставим второе уравнение в первое:
(g+7) + g = 41
2 г + 7 = 41
2 г = 34
g = 17
Далее рассмотрим вероятность «сухой» победы в зависимости от предполагаемого количества очков каждой команды за сезоны с 1983 по 2012 год. Я пропустил все строки, где размер выборки был равен нулю.
Вероятность «сухой» победы
| Оцененный Баллы | Размер выборки | Сухие матчи | Соотношение |
|---|---|---|---|
| 5.25 | 1 | 0 | 0,0% |
| 6.50 | 1 | 0 | 0,0% |
| 7.75 | 1 | 0 | 0,0% |
| 8.00 | 1 | 0 | 0,0% |
| 8.25 | 3 | 0 | 0,0% |
| 8.50 | 2 | 0 | 0,0% |
| 8.75 | 2 | 0 | 0,0% |
| 9.00 | 2 | 0 | 0,0% |
| 9.50 | 4 | 0 | 0,0% |
| 9.75 | 6 | 1 | 16,7% |
| 10.00 | 10 | 1 | 10,0% |
| 10.25 | 7 | 0 | 0,0% |
| 10.50 | 14 | 2 | 14,3% |
| 10.75 | 7 | 1 | 14,3% |
| 11.00 | 13 | 1 | 7,7% |
| 11.25 | 21 | 1 | 4,8% |
| 11.50 | 22 | 3 | 13,6% |
| 11.75 | 23 | 1 | 4,3% |
| 12.00 | 34 | 2 | 5,9% |
| 12.25 | 36 | 7 | 19,4% |
| 12.50 | 41 | 3 | 7,3% |
| 12.75 | 39 | 4 | 10,3% |
| 13.00 | 55 | 1 | 1,8% |
| 13.25 | 58 | 5 | 8,6% |
| 13.50 | 78 | 1 | 1,3% |
| 13.75 | 89 | 5 | 5,6% |
| 14.00 | 92 | 4 | 4,3% |
| 14.25 | 108 | 7 | 6,5% |
| 14.50 | 117 | 8 | 6,8% |
| 14.75 | 141 | 7 | 5,0% |
| 15.00 | 160 | 7 | 4,4% |
| 15.25 | 160 | 7 | 4,4% |
| 15.50 | 213 | 7 | 3,3% |
| 15.75 | 198 | 11 | 5,6% |
| 16.00 | 206 | 6 | 2,9% |
| 16.25 | 221 | 12 | 5,4% |
| 16.50 | 241 | 10 | 4,1% |
| 16.75 | 273 | 7 | 2,6% |
| 17.00 | 306 | 8 | 2,6% |
| 17.25 | 305 | 8 | 2,6% |
| 17.50 | 306 | 10 | 3,3% |
| 17.75 | 323 | 4 | 1,2% |
| 18.00 | 299 | 8 | 2,7% |
| 18.25 | 332 | 8 | 2,4% |
| 18.50 | 309 | 9 | 2,9% |
| 18.75 | 307 | 7 | 2,3% |
| 19.00 | 356 | 8 | 2,2% |
| 19.25 | 389 | 5 | 1,3% |
| 19.50 | 361 | 5 | 1,4% |
| 19.75 | 343 | 6 | 1,7% |
| 20.00 | 402 | 8 | 2,0% |
| 20.25 | 379 | 6 | 1,6% |
| 20.50 | 359 | 3 | 0,8% |
| 20.75 | 353 | 5 | 1,4% |
| 21.00 | 344 | 1 | 0,3% |
| 21.25 | 317 | 3 | 0,9% |
| 21.50 | 341 | 2 | 0,6% |
| 21.75 | 331 | 1 | 0,3% |
| 22.00 | 369 | 1 | 0,3% |
| 22.25 | 336 | 0 | 0,0% |
| 22.50 | 316 | 2 | 0,6% |
| 22.75 | 280 | 3 | 1,1% |
| 23.00 | 311 | 1 | 0,3% |
| 23.25 | 290 | 3 | 1,0% |
| 23.50 | 279 | 1 | 0,4% |
| 23.75 | 255 | 1 | 0,4% |
| 24.00 | 246 | 1 | 0,4% |
| 24.25 | 219 | 0 | 0,0% |
| 24.50 | 230 | 2 | 0,9% |
| 24.75 | 230 | 1 | 0,4% |
| 25.00 | 212 | 2 | 0,9% |
| 25.25 | 207 | 0 | 0,0% |
| 25.50 | 176 | 1 | 0,6% |
| 25.75 | 154 | 0 | 0,0% |
| 26.00 | 154 | 1 | 0,6% |
| 26.25 | 113 | 0 | 0,0% |
| 26.50 | 137 | 0 | 0,0% |
| 26.75 | 122 | 0 | 0,0% |
| 27.00 | 95 | 0 | 0,0% |
| 27.25 | 98 | 0 | 0,0% |
| 27.50 | 83 | 0 | 0,0% |
| 27.75 | 81 | 0 | 0,0% |
| 28.00 | 82 | 0 | 0,0% |
| 28.25 | 55 | 1 | 1,8% |
| 28.50 | 56 | 0 | 0,0% |
| 28.75 | 51 | 0 | 0,0% |
| 29.00 | 48 | 0 | 0,0% |
| 29.25 | 34 | 0 | 0,0% |
| 29.50 | 24 | 0 | 0,0% |
| 29.75 | 25 | 0 | 0,0% |
| 30.00 | 24 | 0 | 0,0% |
| 30.25 | 21 | 0 | 0,0% |
| 30.50 | 18 | 0 | 0,0% |
| 30.75 | 23 | 0 | 0,0% |
| 31.00 | 16 | 0 | 0,0% |
| 31.25 | 15 | 0 | 0,0% |
| 31.50 | 8 | 0 | 0,0% |
| 31.75 | 3 | 0 | 0,0% |
| 32.00 | 6 | 0 | 0,0% |
| 32.25 | 7 | 0 | 0,0% |
| 32.50 | 6 | 0 | 0,0% |
| 32.75 | 3 | 0 | 0,0% |
| 33.00 | 4 | 0 | 0,0% |
| 33.25 | 6 | 0 | 0,0% |
| 33.50 | 5 | 0 | 0,0% |
| 34.75 | 4 | 0 | 0,0% |
| 35.00 | 2 | 0 | 0,0% |
| 35.50 | 1 | 0 | 0,0% |
| 36.00 | 2 | 0 | 0,0% |
| 36.25 | 1 | 0 | 0,0% |
| 36.50 | 1 | 0 | 0,0% |
| 37.25 | 1 | 0 | 0,0% |
| 37.75 | 2 | 0 | 0,0% |
| 42.25 | 1 | 0 | 0,0% |
Следующие шаги слишком сложны, чтобы объяснять их здесь, но я разработал формулу для вероятности нулевой победы, учитывая количество оцененных точек.
p = Предполагаемое количество точек.
x = 1,562545 - 0,302485 * p
Вероятность «сухой» победы = e x /(1+e x )
На следующем графике показана фактическая и расчетная вероятность «сухой» победы при разнице очков от 14 до 22.
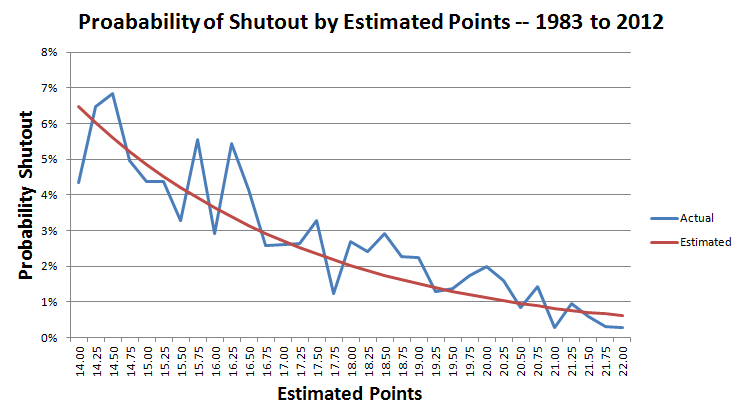
В рассматриваемой игре "Джайентс" рассчитывали набрать 17 очков.
Используя формулу, приведенную выше в таблице:
x = 1,562545 - 0,302485 * 17 = -3,579706
Вероятность «сухой» победы = exp(-3,579706)/( exp(-3,579706)+1) = 2,71%. Точнее, 0,0271275.
Учитывая, что автосалону пришлось бы заплатить 420 000 долларов в случае, если бы «Джайентс» не смогли забить ни одного гола, справедливая стоимость полиса составила бы 420 000 × 0,0271275 = 11 394 доллара. Обычно страховые компании, страхующие необычные акции, подобные этой, удваивают справедливую стоимость, поэтому я ожидал увидеть премию в размере 22 788 долларов. Таким образом, премия в 7000 долларов, которую заплатил автосалон, была невероятно выгодной. Если бы начальник проверил расчеты, я бы не хотел оказаться на месте того, кто рассчитал эту премию в 7000 долларов.
Этот вопрос был поднят и обсуждался на моём форуме в Wizard of Vegas .
Каково доказательство того, что наибольшего простого числа не существует?
Давайте на минуту предположим, что существует наибольшее простое число. Мы можем пронумеровать эти простые числа: p1=2, p2=3, p3=5, p4=7, ... pL = наибольшее простое число.
Теперь определим число x = p1*p2*p3*p4*...*pL + 1.
Простое число означает, что никакое другое, меньшее простое число, не делится на него без остатка.
Если разделить x на p1, p2, p3, ... pL, то каждый раз получим остаток 1.
Можно предположить, что простое число, большее pL, делит x нацело. Да, но тогда вы бы нашли простое число, большее так называемого наибольшего простого числа. Если нет, то x становится новым наибольшим простым числом, доказывая первоначальную гипотезу о существовании наибольшего простого числа методом от противного.
Этот вопрос был задан и обсуждался на моём форуме, посвящённом игре Wizard of Vegas .
Согласны ли вы со статьей под названием«Математика говорит, что вам следует купить лотерейный билет Mega Millions прямо сейчас » на сайте Business Insider?
Нет, я с этим не согласен. Это ужасная журналистская работа, и Business Insider должно быть стыдно за это.
Для начала, статья была опубликована 17 декабря 2013 года, до розыгрыша джекпота в размере 636 миллионов долларов, который состоялся в тот вечер. Давайте рассмотрим математические расчеты, чтобы оценить стоимость билета в 1 доллар. В следующей таблице показаны вероятности и ожидаемая прибыль всех возможных исходов для джекпота в 636 миллионов долларов, до учета таких факторов, как единовременный штраф, налоги и распределение джекпота. Три наиболее вероятных значения представлены в научной нотации, поскольку эти числа очень малы.
Mega Millions — Джекпот в размере 636 миллионов долларов.
| Ловить | Мегабол | Платит | Комбинации | Вероятность | Возвращаться |
|---|---|---|---|---|---|
| 5 | Да | 636 000 000 долларов США | 1 | 3.86E-09 | 2.456634 |
| 5 | Нет | 1 000 000 долларов США | 14 | 5.41E-08 | 0.054077 |
| 4 | Да | 5000 долларов | 350 | 1.35E-06 | 0.006760 |
| 4 | Нет | 500 долларов | 4900 | 0.000019 | 0.009463 |
| 3 | Да | 50 долларов | 24,150 | 0.000093 | 0.004664 |
| 3 | Нет | 5 долларов | 338,100 | 0.001306 | 0.006530 |
| 2 | Да | 5 долларов | 547,400 | 0.002114 | 0.010572 |
| 1 | Да | 2 доллара | 4 584 475 | 0.017708 | 0.035416 |
| 0 | Да | 1 доллар | 12,103,014 | 0.046749 | 0.046749 |
| Неудачник | 0 долларов | 241,288,446 | 0.932008 | 0.000000 | |
| Общий | 258,890,850 | 1.000000 | 2.630865 | ||
Это показывает, что за билет стоимостью 1 доллар можно получить 2,630864 доллара прибыли. После вычета доллара, потраченного на билет, ожидаемая прибыль составляет 1,630864 доллара. Business Insider получает 1,632029 доллара. Разница составляет 0,001164 доллара, но это не имеет большого значения.
Однако есть три фактора, которые значительно снижают его значение:
- Штраф в виде единовременной выплаты.
- Налоги.
- Разделение джекпота.
Давайте рассмотрим их по очереди.
Крупные прогрессивные джекпоты лотерей обычно выплачиваются в виде аннуитета в течение примерно 30 лет, включая Mega Millions. Если победитель хочет получить все деньги сразу, что делают большинство, ему приходится соглашаться на значительное уменьшение суммы выигрыша. Это справедливо, поскольку доллар сегодня стоит больше, чем доллар в будущем. В случае розыгрыша 17 декабря 2013 года общая сумма выигрыша была уменьшена до 347,6 миллионов долларов, или 54,65% от заявленного джекпота.
Теперь давайте рассмотрим налоги. Самая высокая федеральная предельная ставка подоходного налога составляет 39,6%. Налоги штатов варьируются от 0% до 12,3%, поэтому давайте предположим, что в среднем это 6%. После вычета 45,6% налогов у нас остается 189,1 миллиона долларов.
Теперь самая сложная часть — распределение джекпота. Следует отметить, что начиная с розыгрыша 22 октября 2013 года, правила лотереи Mega Millions изменились на формат 75-15, где разыгрываются пять чисел от 1 до 75, а затем одно число из отдельного пула от 1 до 15. Это снизило шансы на выигрыш до 1 к 258 890 850, очевидно, в попытке увеличить джекпоты. Рассмотрев только 17 розыгрышей с тех пор, используя данные о джекпотах и продажах с сайта LottoReport.com , я обнаружил экспоненциальную зависимость между размером джекпота и спросом. Кстати, то же самое я обнаружил и для лотереи Powerball . Используя экспоненциальную регрессию, моя формула для общего количества проданных билетов (в миллионах) выглядит так: 12,422 × exp(0,0052 × j), где j — размер джекпота (в миллионах). Например, при джекпоте в 636 миллионов долларов ожидаемая выручка составила бы 12,422 * exp(0,0052*636) = 339,2 (миллион). Фактическая выручка составила 337 миллионов долларов, так что довольно близко к истине.
Исходя из фактического количества проданных билетов — 336 545 306, — мы можем ожидать 336 545 306 / 258 890 850 = 1,300 победителей. Важный вопрос: если вы выиграете, с каким количеством других людей вы сможете разделить выигрыш? На него легко ответить, используя распределение Пуассона. При среднем значении 1,3 победителя вероятность того, что выиграет ровно x человек, равна exp(1,3)×1,3 x /fact(x). В следующей таблице показана вероятность того, что выиграет от 0 до 10 других человек, ваша доля джекпота в каждом случае и ожидаемая доля, если вы выиграете.
Ожидаемая доля джекпота в среднем составляет 1,3 доли от других победителей.
| Другие победители | Вероятность | Доля джекпота | Ожидаемая доля |
|---|---|---|---|
| 10 | 0.000001 | 0.090909 | 0.000000 |
| 9 | 0.000008 | 0.100000 | 0.000001 |
| 8 | 0.000055 | 0.111111 | 0.000006 |
| 7 | 0.000339 | 0.125000 | 0.000042 |
| 6 | 0.001827 | 0.142857 | 0.000261 |
| 5 | 0.008431 | 0.166667 | 0.001405 |
| 4 | 0.032429 | 0.200000 | 0.006486 |
| 3 | 0.099786 | 0.250000 | 0.024946 |
| 2 | 0.230283 | 0.333333 | 0.076761 |
| 1 | 0.354295 | 0.500000 | 0.177148 |
| 0 | 0.272545 | 1.000000 | 0.272545 |
| Общий | 1.000000 | 0.559602 |
В нижней правой ячейке указано, что вы можете рассчитывать на то, что оставите себе 55,96% денег, а остальные 44,04% достаются тем самым другим победителям, с которыми вам придется делиться.
Теперь наш джекпот в 636 миллионов долларов сократился до 189,1 × 55,96% = 105,8 миллионов долларов. Давайте посмотрим, как будет выглядеть таблица выплат с этой суммой джекпота.
Mega Millions — Джекпот в размере 105,8 миллионов долларов.
| Ловить | Мегабол | Платит | Комбинации | Вероятность | Возвращаться |
|---|---|---|---|---|---|
| 5 | Да | 105 800 000 долларов США | 1 | 3.86E-09 | 0.408666 |
| 5 | Нет | 1 000 000 долларов США | 14 | 5.41E-08 | 0.054077 |
| 4 | Да | 5000 долларов | 350 | 1.35E-06 | 0.006760 |
| 4 | Нет | 500 долларов | 4900 | 0.000019 | 0.009463 |
| 3 | Да | 50 долларов | 24,150 | 0.000093 | 0.004664 |
| 3 | Нет | 5 долларов | 338,100 | 0.001306 | 0.006530 |
| 2 | Да | 5 долларов | 547,400 | 0.002114 | 0.010572 |
| 1 | Да | 2 доллара | 4 584 475 | 0.017708 | 0.035416 |
| 0 | Да | 1 доллар | 12,103,014 | 0.046749 | 0.046749 |
| Неудачник | 0 долларов | 241,288,446 | 0.932008 | 0.000000 | |
| Общий | 258,890,850 | 1.000000 | 0.582898 | ||
В нижней правой ячейке показана ожидаемая доходность в 58,29%. Другими словами, ваши инвестиции в 1 доллар могут принести около 58 центов обратно, при ожидаемом убытке, или преимуществе казино, около 42%. Похоже ли это на расчеты, которые говорят о необходимости купить билет?
Согласно статье, "пока продано менее 730 миллионов билетов, что сейчас довольно вероятно, ожидаемая стоимость билета должна быть положительной, поэтому вам следует подумать о покупке билета Mega Millions сегодня".
Объем продаж был значительно меньше 730 миллионов, и это все равно было ужасно невыгодно. Однако, справедливости ради, в статье далее говорилось следующее:
«Имейте в виду, что к этому анализу есть много оговорок. Налоги, скорее всего, сильно сократят ваш ожидаемый выигрыш — федеральное правительство заберет около 40%, а ваш родной штат — от 0% до примерно 13%».
«Многие покупают билеты, и, как обсуждалось выше, это значительно увеличит вероятность ничьей и, соответственно, снизит размер выигрыша». — Business Insider
Это довольно существенные оговорки! Их не следует просто упомянуть вскользь в конце, а нужно учитывать при анализе с самого начала.
Не то чтобы вы спрашивали, но, по моим расчетам, играть в Mega Millions никогда не стоит. Учитывая экспоненциальный спрос на билеты, основанный на размере джекпота, я считаю оптимальным временем для игры джекпот в 545 миллионов долларов. При джекпотах большего размера вам придется делить его со слишком многими другими победителями. При таком размере джекпота игрок может рассчитывать на доход в 60,2% или убыток в 39,8%. Это лучший результат, которого можно достичь.
В заключение, нет, я не согласен с Business Insider в том, что издание обманывает читателей сенсационным заголовком и не проводит должного анализа налогов и распределения джекпотов.
Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .


