Спросите Волшебника #402

На вашем калькуляторе для видеопокера 9-6 Jacks or Better указано общее количество комбинаций — 1 661 102 543 100. В то же время на вашей странице Jacks or Better указано 19 933 230 517 200. Мне кажется, количество комбинаций должно быть одинаковым. Интересно, почему такая разница? Выигрыш (0,995439) кажется одинаковым.

IndyJeffrey

Да, оба источника посвящены одной и той же игре.

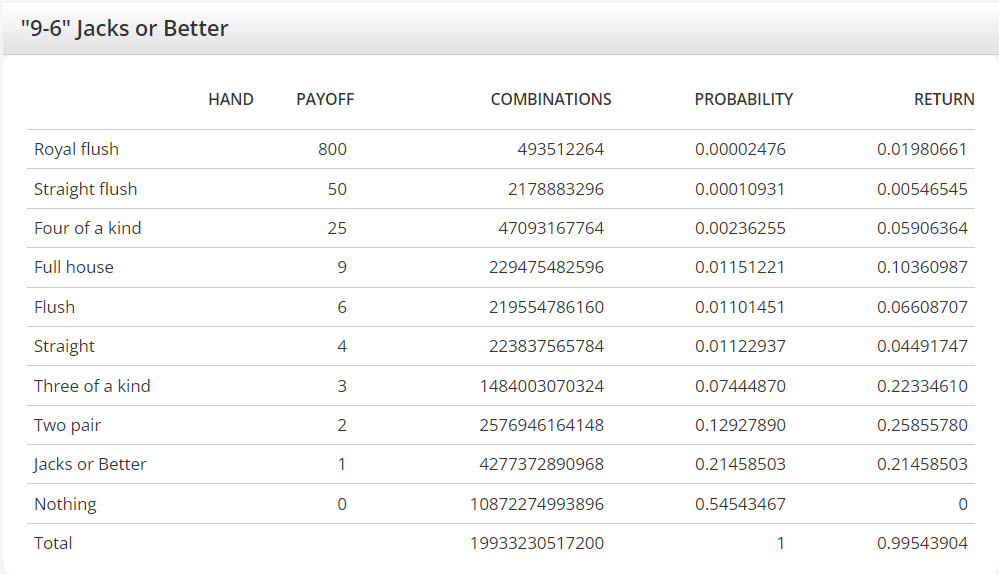
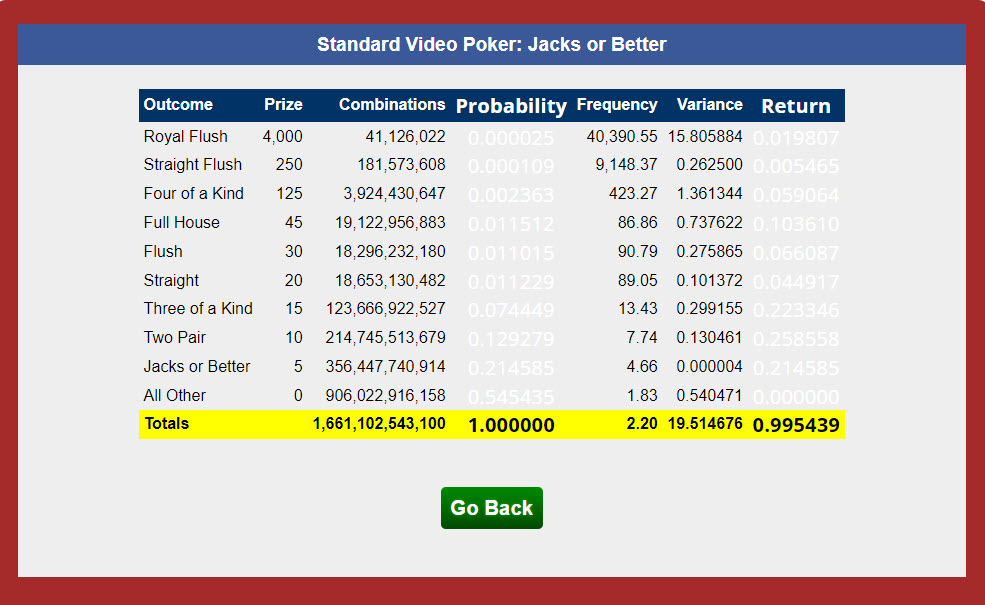
Причина кроется в способе анализа игры. Чем больше карт игрок сбрасывает, тем больше комбинаций при розыгрыше. В следующей таблице показано количество комбинаций при розыгрыше, то есть количество способов выбрать количество сброшенных карт из 47 оставшихся в колоде.

Отбросы	Комбинации при ничьей	Взвешивание
0	1	7 669 695
1	47	163,185
2	1081	7095
3	16,215	473
4	178,365	43
5	1 533 939	5

Наименьшее общее кратное чисел 1, 47, 1081, 16215, 178365 и 1533939 равно 7669695.

Важно, чтобы каждая стартовая рука имела одинаковый суммарный вес. Для этого я применяю к каждой руке весовой коэффициент в зависимости от количества сброшенных карт. Этот весовой коэффициент указан в правом столбце таблицы выше. Произведение количества комбинаций в раздаче и весового коэффициента всегда будет равно 7 669 695.

Существует комбинация (52,5) = 52!/(47!*5!) = (48*49*50*51*52)/(1*2*3*4*5) = 2 598 960 способов выбрать пять карт из 52. Таким образом, общее количество комбинаций в видеопокере, согласно моему анализу, составляет combin(52,5)*combin(47,5)*5 = 2 598 960 * 7 669 695 = 19 933 230 517 200. Именно поэтому вы так часто видите это число в качестве общего количества комбинаций в моих таблицах возврата.

Почему же калькулятор показывает 1 661 102 543 100, спросите вы? Этот калькулятор создал гений программирования видеопокера JB. Он добавил шаг для нахождения наибольшего общего кратного комбинаций каждой руки. Это наименьшее общее кратное обычно составляло 12. Каким бы оно ни было, он делил каждое число комбинаций на это наименьшее общее кратное. Я думаю, это потому, что он предпочитает, чтобы числа были как можно меньше, не жертвуя при этом точностью.

Есть резиновая лента длиной один метр, на одном конце которой находится муравей. Каждый день муравей проходит один сантиметр. В конце дня резиновая лента растягивается на один метр. Сколько времени потребуется муравью, чтобы добраться до другого конца?

анонимный

Сразу предупреждаю, это довольно сложная задача. В спойлере ниже я приведу несколько подсказок, которые помогут вам её решить.

[спойлер=Подсказки]

Гармонический ряд

Постоянная Эйлера (не путать с числом Эйлера)

[/спойлер]

15,092,688,622,113,800,000,000,000,000,000,000,000,000,000

Вот моё решение (PDF).

Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .

Недавно мы с другом получили два из трёх символов Megabucks. Какова вероятность этого?

Hot Blonde от Las Vegas

Согласно информации на моей странице о Megabucks , общий вес каждого барабана составляет 368, при этом символы Megabucks имеют вес 1. Таким образом, вероятность выпадения символов Megabucks на любом барабане составляет 1/368.

Вероятность получить ровно 2 из 3 составляет 3 × (1/368) * (1/368) × (367/368) ≈ 0,0000220924 ≈ 1/45264.