WOO logo

Wizard рекомендует

Спросите Волшебника #422

Допустим, в игре в блэкджек используется бесконечное количество колод, допускается бесконечное повторное разделение карт, и игрок разделит любую пару. Какова вероятность того, что игрок сыграет любое заданное количество финальных раздач?

анонимный

Вероятность повторного разделения на n рук равна (комбинация(2*(n-1),n-1)/n) × (1/13)^(n-1) × (12/13)^n. Для получения дополнительной информации о первом члене, с которым мне понадобилась помощь, обратитесь к каталанским числам .

В следующей таблице показана вероятность выпадения от 1 до 20 финальных раздач. В столбце «секунды» указано количество «деревьев», которое в приведенном выше выражении соответствует каталанскому числу.

Руки Деревья Вероятность
1 1 0.9230769230769
2 1 0.0655439235321
3 2 0.0093080128093
4 5 0.0016523099661
5 14 0.0003285065968
6 42 0.0000699777366
7 132 0.0000156163334
8 429 0.0000036037693
9 1430 0.0000008529631
10 4862 0.0000002059225
11 16796 0.0000000505114
12 58786 0.0000000125531
13 208012 0.0000000031540
14 742900 0.0000000007998
15 2674440 0.0000000002045
16 9694845 0.0000000000526
17 35357670 0.0000000000136
18 129644790 0.0000000000035
19 477638700 0.0000000000009
20 1767263190 0.0000000000002

Я слышал, что существует бесконечное количество пифагоровых троек. Есть ли какой-нибудь формульный способ их найти?

анонимный

Да, существует бесконечное количество уникальных пифагоровых троек! Для тех, кто не знаком с этим термином, это прямоугольные треугольники, каждая сторона которых является целым числом. 3-4-5 — самая известная из них. Чтобы получить уникальное (другими словами, неприводимое) множество пифагоровых троек, выберите любые целые значения для a и b, где a < b, и одно из них нечетное, а другое четное.

  • Нога 1 = b 2 - a 2
  • Вторая нога = 2ab
  • Гипотенуза = a² + b²

В следующей таблице показаны все неприводимые пифагорейские тройки, у которых все стороны равны 101 или меньше.

а,б Этап 1 Этап 2 Гипотенуза
1,2 3 4 5
1,4 8 15 17
1,6 12 35 37
1,8 16 63 65
1,10 20 99 101
2,3 5 12 13
2,5 20 21 29
2,7 28 45 53
2,9 36 77 85
3,4 7 24 25
3,6 27 36 45
3,8 48 55 73
4,5 9 40 41
4,7 33 56 65
4,9 65 72 97
5,6 11 60 61
5,8 39 80 89
6,7 13 84 85

Какова вероятность того, что при выпадении любой суммы на двух игральных костях, кроме семерки, она выпадет как минимум дважды, прежде чем выпадет семерка?

Garrison

Секрет подобных задач заключается в том, что вероятность одинакова, если промежуток времени между бросками подчиняется экспоненциальному распределению со средним значением, равным 1. В этом случае её можно выразить следующей формулой.

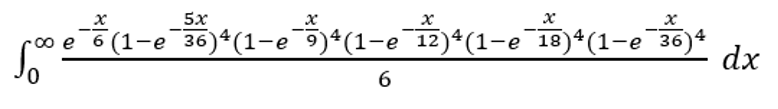
В текстовом виде: exp(-x/6)*(1-exp(-5x/36))^4*(1-exp(-4x/36))^4*(1-exp(-3x/36))^4*(1-exp(-2x/36))^4*(1-exp(-1x/36))^4/6

Для решения подобных интегралов я рекомендую этот калькулятор интегралов .

Ответ равен 7864581698887803455719/10946915593544650625105200 =~ 0.0007184290069364848.