Крэпс - Кубики и броски
Я хотел бы узнать, как изменить бросок кубиков в игре в крэпс, чтобы каждый раз выпадало 7 или 11? Можете помочь? Спасибо.
Измените игральную кость так, чтобы на одной стороне каждой игральной кости была шестерка, а на другой — только единицы и пятерки.
Верите ли вы, что «выдача желаемого за действительное» со стороны игроков может повлиять на исход игры? Заметьте, меня не интересует РАЗМЕР этого влияния, а только ваше философское мнение. Также, считаете ли вы, что способ, которым игрок бросает кости в крэпсе, может вызвать предвзятость (хорошую или плохую) в исходе игры? Как всегда, ваш сайт ПОТРЯСАЮЩИЙ.
Спасибо за добрые слова. Нет, я не думаю, что выдача желаемого за действительное помогает в казино, при прочих равных условиях.
Вопрос о влиянии игральных костей является предметом жарких дебатов. Лично я отношусь к этому очень скептически. Перечитывая этот ответ в 2013 году, я до сих пор не вижу убедительных доказательств того, что кто-либо может повлиять на результат настолько, чтобы получить преимущество.
Мне просто интересно ваше мнение о возможности изменения таблицы частот в игре в кости путем предварительной настройки игральных костей.
Я отношусь к этому очень скептически. Некоторые эксперименты на эту тему я описываю в приложении 3 к моей книге о крэпсе .
Недавно я узнал кое-что о стратегиях расстановки кубиков в крэпсе. Некоторые считают, что можно установить кубики определённым образом перед броском, и, удерживая бросок кубиков только на одной оси вращения, можно уменьшить количество возможных семерок при определённых наборах кубиков. Я хотел бы узнать, есть ли в этом доля правды или это просто заблуждение.
Я в это не верю. До сих пор я не видел ни одного уважаемого мною человека, который бы одобрил этот метод, и никаких доказательств его эффективности. Хотя я не исключаю полностью такую возможность, я отношусь к этому крайне скептически. Я, может быть, и живу в Неваде, но когда дело доходит до таких вещей, как расстановка игральных костей, я из Миссури, «покажите мне», что это работает.
Действительно ли игральные кости беспристрастны? Кажется, что грани с большими числами, имеющие больше отверстий, будут легче, чем грани с меньшими числами и меньшим количеством отверстий. Это, по-видимому, предполагает, что более тяжелые грани с большей вероятностью упадут лицевой стороной вниз, а грани с большими числами — лицевой стороной вверх. Я могу представить себе систему игры в кости, которая могла бы попытаться использовать этот принцип, но мне интересно, сработает ли это на самом деле. Что вы думаете?
В случае с обычными игральными костями, такими, какие используются в настольных играх, это верно. Однако в игральных костях казино есть инкрустированные точки. На заводе сверлят отверстия для точек, а затем вставляют в них белые точки той же плотности, что и сама игральная кость. Таким образом, игральная кость по сути представляет собой идеальный куб. Даже если бы они использовали обычные игральные кости из настольной игры, я сомневаюсь, что это смещение было бы достаточно сильным, чтобы перевесить преимущество казино.
Верите ли вы, что бросок костей за столом для игры в крэпс в казино действительно случаен, как это бывает с генератором случайных чисел, или же есть хорошие и плохие игроки, которые бросают кости либо из-за «механики» броска, либо из-за просто небрежного броска (например, короткие броски)? Если в реальном мире игра в крэпс не является по-настоящему случайной, как я могу этим воспользоваться?
Я думаю, что не бывает от природы плохих игроков в кости. За исключением, возможно, нескольких профессионалов, все броски костей можно считать абсолютно случайными. Существуют семинары о том, как преодолеть преимущество казино в крэпсе с помощью прецессионного броска, но я не делаю никаких заявлений за или против них. Я пока не видел достаточно доказательств ни в пользу, ни против.
В октябрьском номере журнала Casino Player Фрэнк Скоблете написал статью о контролируемой игре в кости, где вы утверждаете, что проиграли 1800 долларов Стэнфорду Вонгу, когда тот выбросил всего 74 семерки из 500 бросков. Почему вы сделали ставку на такую маленькую выборку (500)? Человек, утверждающий, что умеет контролировать кости, должен быть готов продемонстрировать свое мастерство, сделав как минимум 50 000 бросков. Не ошибаюсь ли я, считая, что 500 бросков — это настолько маленькая выборка, что может произойти практически что угодно?
Я проиграл 1800 долларов другому автору статей об азартных играх, а не Стэнфорду. Я бы предпочел больше бросков, но было очевидное ограничение по времени. Предполагая один бросок в минуту, потребовалось бы 34,7 дня, чтобы бросить кости 50 000 раз. Я не тот, кто выбрал 500, но это показалось разумным компромиссом между большим размером выборки и временем. Вы правы, 500 слишком мало, чтобы убедительно доказать за или против влияния бросков костей, но 500 бросков лучше, чем ноль.
Я знаю, вы скептически относитесь к контролю над броском кубиков. Я тренируюсь в расстановке кубиков и контролируемом броске уже 3 месяца. Какова вероятность выпадения 78 семерок из 655 случайных бросков? Спасибо за помощь :)
Для большого количества бросков мы можем использовать аппроксимацию кривой Гаусса. Ожидаемое количество семерок из 655 бросков составляет 655 × (1/6) = 109,1667. Дисперсия равна 655 × (1/6) × (5/6) = 90,9722. Стандартное отклонение равно sqr(90,9722) = 9,5379. Ваши 78 семерок на 109,1667 − 78 = 31,1667 меньше ожидаемого значения. Это (31,1667 - 0,5)/9,5379 = 3,22 стандартных отклонения ниже ожидаемого значения. Вероятность отклонения на 3,22 или более стандартных отклонений от ожидаемого значения составляет 0,000641, или 1 к 1560. Этот результат я получил в Excel, используя формулу normsdist(-3.22).
Речь идёт о контроле над игральными костями в крэпсе. Ранее вы обсуждали Стэнфордский эксперимент Вонга , заявив: «Условием пари было то, смогут ли игроки, отличающиеся точностью бросков, выбросить менее 79,5 семёрок за 500 бросков костей. Ожидаемое число в случайной игре составило бы 83,33. Вероятность выпадения 79 или менее семёрок за 500 случайных бросков составляет 32,66%... Вероятность выпадения 74 или менее семёрок за 500 случайных бросков составляет 14,41%».
Вопрос, который у меня возникает по поводу этой ставки, заключается в том, что 14,41% все еще не является «статистически значимым» [т.е. p < 0,05], что обычно понимается как отклонение более чем на два стандартных отклонения от среднего значения — или вероятность того, что менее *совокупных* 5% событий произойдет случайным образом на любом из концов ряда.
Сколько семерок должно выпасть за 500 бросков, чтобы можно было сказать, что вероятность того, что результат был полностью случайным (то есть, статистически значимым), составляет менее 2,5%?
Большое спасибо! И кстати, ваш сайт — БЕЗУСЛОВНО ЛУЧШИЙ сайт по теме коэффициентов и вероятностей в азартных играх, который я нашел... Продолжайте в том же духе!!!
Спасибо за добрые слова. Не следует говорить, что вероятность того, что броски были неслучайными, равна p. Правильнее было бы сформулировать это так: вероятность того, что случайная игра даст такой результат, равна p. Никто не ожидал, что 500 бросков что-либо докажут или опровергнут. Не я установил линию в 79,5 семерок, но сомневаюсь, что она была выбрана с целью статистической значимости; скорее, я подозреваю, что это была точка, при которой обе стороны согласились бы на пари.
Уровень значимости 2,5% составляет 1,96 стандартных отклонений от ожидаемого значения. Это можно рассчитать с помощью формулы =normsinv(0,025) в Excel. Стандартное отклонение для 500 бросков равно sqr(500*(1/6)*(5/6)) = 8,333. Таким образом, 1,96 стандартных отклонений — это 1,96 * 8,333 = 16,333 бросков в сторону меньше ожидаемого значения. Ожидаемое количество семерок в 500 бросках составляет 500*(1/6) = 83,333. Таким образом, 1,96 стандартных отклонений в сторону меньше этого значения равно 83,333 − 16,333 = 67. Проверив это с помощью биномиального распределения, получаем, что точная вероятность выпадения 67 или менее семерок составляет 2,627%.
Три года назад в рубрике «Спроси волшебника » вы написали: «Вы правы, 500 бросков — это слишком мало, чтобы убедительно доказать за или против влияния на результаты бросков кубиков, но 500 бросков лучше, чем ноль». Можете ли вы описать, что вам потребуется от предполагаемого «влиятеля на результаты бросков кубиков» в эксперименте, чтобы вы почувствовали себя достаточно уверенно, чтобы начать делать на него значительные ставки? Я спрашиваю, потому что миллиард бросков — это хороший ориентир для «надежных» результатов в некоторых симуляторах блэкджека. При самом эффективном (то есть требующем наименьшего количества бросков) экспериментальном дизайне, сколько бросков должен сделать игрок, чтобы быть уверенным, что он влияет на результаты? Я понимаю, что ответ будет зависеть от мастерства игрока, но вы меня понимаете. Если вам потребуется миллион бросков даже в лучшем случае, это не будет стоящим делом.
Нет определенной точки, после которой можно заслужить уверенность. Это вопрос степени. Во-первых, я бы спросил, что именно проверяется и что, по оценке стрелка, произойдет. В любом тесте возможны две ошибки. Опытный стрелок может провалить тест из-за невезения, а случайный стрелок может пройти его из-за удачи. Из этих двух я бы предпочел избежать ложноположительного результата. Думаю, разумный тест должен устанавливать вероятность ложноотрицательного результата примерно на уровне 5%, а ложноположительного — примерно на уровне 1%.
Например, предположим, что истец утверждает, что в среднем выпадает одна семерка каждые семь бросков игральных костей. Случайный стрелок в среднем выбрасывает одну семерку каждые шесть бросков. Методом проб и ошибок я обнаружил, что для проверки, удовлетворяющей обоим этим критериям, необходимо бросить кости 3600 раз и получить не более 547 семерок, или одну семерку на 6,58 бросков.
У одного из семи стрелков в среднем должно выпадать 514,3 семерки, со стандартным отклонением 21,00. Используя гауссову аппроксимацию, вероятность того, что такой опытный стрелок выбросит 548 или более семерок (ложноотрицательный результат), составляет 5,7%. У случайного стрелка в среднем должно выпадать 600 семерок, со стандартным отклонением 22,36. Вероятность того, что случайный стрелок пройдет тест (ложноположительный результат), составляет 0,94%. На графике ниже показаны возможные результаты для опытных и случайных стрелков. Если результаты находятся слева от зеленой линии, то я бы посчитал, что стрелок прошел тест, и сделал бы на него ставку.
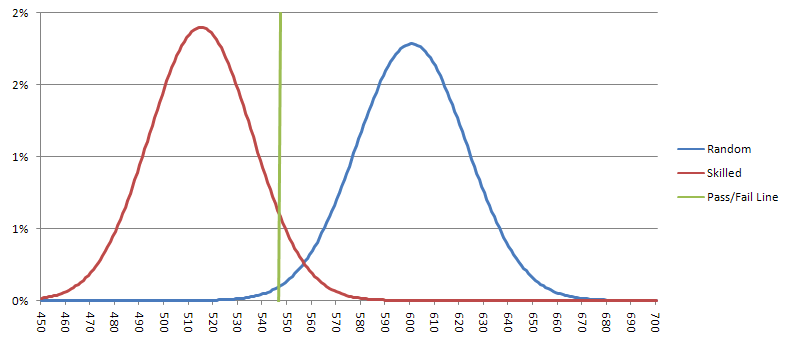
Практическая дилемма заключается в том, что если предположить два броска в минуту, то на проведение теста потребуется 30 часов. Возможно, я мог бы быть более либеральным в отношении уровня значимости, чтобы сократить затраты времени, но результаты не были бы такими убедительными. Я думаю, что настало время для более масштабного теста, чем эксперимент Вонга с 500 бросками.
Сегодня в новостях: женщина в Атлантик-Сити бросила две игральные кости 154 раза подряд, прежде чем выпала семерка, в казино Borgata . Это значит, что она бросила две кости 154 раза, и ни одной семерки не выпала. Поэтому я взял (30/36) 154 и получил шансы более 1,5 триллиона к 1. Вероятность выиграть в лотерею Mega Millions примерно в 9000 раз выше, чем совершить марафон из 154 бросков костей подряд, не выпавших семерки. Учитывая астрономическую маловероятность этого, и учитывая, что людей осуждают на основании ДНК-доказательств, вероятность ложного совпадения которых составляет всего миллиард к одному, насколько сильно вы бы заподозрили мошенничество и предложили бы вы проконсультироваться по этому поводу в Borgata? Я уже позвонил им, назвал свое имя и сказал, чтобы они делали с ним что хотят. Мне интересно ваше мнение.
Во-первых, она бросила кости в общей сложности 154 раза, причём 154-й бросок выпал на семёрку ( Источник: NJ.com ). Однако это не означает, что она ни разу не выбросила семёрку за первые 153 броска. Она могла выбросить их много раз при первом броске. Как я показываю в своей колонке от 3 мая 2003 года , вероятность дойти до 154-го броска составляет 1 к 5,6 миллиардам. Шансы выиграть в Mega Millions составляют 1 к комбинации (56,5)*46 = 175 711 536. Таким образом, дойти до 154 или более бросков примерно в 32 раза сложнее. При достаточном количестве времени и таблицах, которые, как я думаю, существуют, что-то подобное должно было произойти рано или поздно. Поэтому я бы не стал подозревать мошенничество. Я приблизительно оцениваю вероятность того, что это произойдёт в любой конкретный год, примерно в 1%.
См. также мое решение, выраженное в матрицах, на сайте mathproblems.info , задача 204.
Я думаю, что в некоторых казино Лас-Вегаса используют игральные кости, утяжеленные с одной стороны. В качестве доказательства я привожу результаты 244 бросков, которые я собрал в одном из казино на Стрипе. Какова вероятность того, что такие искаженные результаты могут быть получены при использовании честных игральных костей?
| Данные теста Dice | |
| Сумма выпавших кубиков | Наблюдения |
| 2 | 6 |
| 3 | 12 |
| 4 | 14 |
| 5 | 18 |
| 6 | 23 |
| 7 | 50 |
| 8 | 36 |
| 9 | 37 |
| 10 | 27 |
| 11 | 14 |
| 12 | 7 |
| Общий | 244 |
7,7%.
Критерий хи-квадрат идеально подходит для решения подобных задач. Для использования критерия возьмите (ae) ² /e для каждой категории, где a — фактический результат, а e — ожидаемый результат. Например, ожидаемое количество бросков, дающих в сумме 2, из 244 составляет 244 × (1/36) = 6,777778. Если вы не понимаете, почему вероятность выпадения 2 равна 1/36, пожалуйста, прочтите мою страницу об основах вероятности при бросках игральных костей . Для значения хи-квадрат, дающего в сумме 2, a=6 и e=6,777778, поэтому (ae) ² /e = (6-6,777778) ² /6,777778 = 0,089253802.
Результаты критерия хи-квадрат
| Сумма выпавших кубиков | Наблюдения | Ожидал | Хи-квадрат |
| 2 | 6 | 6.777778 | 0.089253 |
| 3 | 12 | 13.555556 | 0.178506 |
| 4 | 14 | 20.333333 | 1.972678 |
| 5 | 18 | 27.111111 | 3.061931 |
| 6 | 23 | 33.888889 | 3.498725 |
| 7 | 50 | 40.666667 | 2.142077 |
| 8 | 36 | 33.888889 | 0.131512 |
| 9 | 37 | 27.111111 | 3.607013 |
| 10 | 27 | 20.333333 | 2.185792 |
| 11 | 14 | 13.555556 | 0.014572 |
| 12 | 7 | 6.777778 | 0.007286 |
| Общий | 244 | 244 | 16.889344 |
Затем возьмите сумму значений в столбце хи-квадрат. В этом примере сумма равна 16,889344. Это называется статистикой хи-квадрат. Число «степеней свободы» на единицу меньше, чем число категорий в данных, в данном случае 11-1=10. Наконец, либо найдите в статистической таблице значение хи-квадрат, равное 10,52, и 10 степеней свободы, либо используйте формулу =chidist(16,889344,10) в Excel. В любом случае вы получите результат 7,7%. Это означает, что вероятность того, что честные игральные кости дадут результаты с таким или более сильным искажением, составляет 7,7%. В итоге, хотя эти результаты более искажены, чем ожидалось, они не настолько, чтобы вызывать какие-либо вопросы. Если вы продолжите этот тест, я бы посоветовал собирать индивидуальные результаты каждой игральной кости, а не их сумму. Следует также отметить, что критерий хи-квадрат неприменим, если ожидаемое число исходов в категории невелико. Обычно используется значение 5, минимальное ожидаемое число.
Что произойдет, если в игре в кости две игральные кости выпадут стопкой? Будет ли это действительный бросок? Если да, то как дилеры объявят, на какое число выпало меньшее число?
Действительность броска зависит от места. В правилах штата Нью-Джерси, касающихся азартных игр, в пункте 19:47-1.9(a) говорится:
Бросок игральных костей считается недействительным, если одна или обе кости выпадают за пределы стола или если одна кость оказывается поверх другой. -- NJ 19:47-1.9(a)
В Пенсильвании действует точно такое же положение, Раздел 537.9(a) :
Бросок игральных костей считается недействительным, если одна или обе кости выпадают за пределы стола или если одна кость оказывается поверх другой. -- PA 537.9(a)
Я спросил дилера по игре в кости в Лас-Вегасе, и он сказал, что здесь это будет считаться действительным броском, если в остальном это правильный бросок. Хотя он никогда не видел, чтобы такое случалось, он сказал, что если бы это произошло, дилеры просто передвинули бы верхнюю кость, чтобы посмотреть, на какое число выпало нижнее число. Однако результат броска нижнего кубика можно определить, не прикасаясь к верхнему и не глядя на него. Вот как это сделать. Во-первых, посмотрев на четыре грани, можно сузить круг возможных вариантов до двух. Вот как это определить, исходя из этих трех вариантов.
- 1 или 6: Ищите цифру 3. Если верхняя точка граничит с 5, то 1 находится сверху. В противном случае, если она граничит с 2, то 6 находится сверху.
- 2 или 5: Ищите цифру 3. Если верхняя точка граничит с 6, то 2 находится сверху. В противном случае, если она граничит с 1, то 5 находится сверху.
- 3 или 4: Ищите цифру 2. Если верхняя точка граничит с 6, то 3 находится сверху. В противном случае, если она граничит с 1, то 4 находится сверху.
Этот вопрос был поднят и обсужден на форуме моего дочернего сайта Wizard of Vegas .
Каково ожидаемое количество бросков двух игральных костей, при которых хотя бы один раз выпадет сумма от 2 до 12?
Этот вопрос был задан на сайте TwoPlusTwo.com, и на него правильно ответил BruceZ . Следующее решение использует тот же метод, что и BruceZ, который заслуживает должного признания. Это сложный ответ, поэтому будьте внимательны.
Для начала рассмотрим ожидаемое количество бросков, необходимых для получения в сумме двух чисел. Вероятность выпадения двойки составляет 1/36, поэтому в среднем потребуется 36 бросков, чтобы получить первую двойку.
Далее рассмотрим ожидаемое количество бросков, необходимых для получения двойки и тройки. Мы уже знаем, что в среднем потребуется 36 бросков, чтобы получить двойку. Если тройка выпадает во время ожидания двойки, то дополнительных бросков для тройки не потребуется. Однако, если нет, то для получения тройки придется бросить больше кубиков.
Вероятность выпадения тройки составляет 1/18, поэтому в среднем потребуется 18 дополнительных бросков, чтобы получить тройку, если сначала выпадет двойка. Учитывая, что существует 1 способ выбросить двойку и 2 способа выбросить тройку, вероятность того, что сначала выпадет двойка, составляет 1/(1+2) = 1/3.
Таким образом, существует вероятность 1/3, что нам потребуется еще 18 бросков, чтобы получить тройку. Следовательно, ожидаемое количество бросков, чтобы получить и двойку, и тройку, составляет 36 + (1/3) × 18 = 42.
Далее, подумайте, сколько еще бросков вам понадобится, чтобы получить четверку. К тому моменту, когда вы выбросите двойку и тройку, если вы еще не получили четверку, вам придется бросить кубики в среднем еще 12 раз, чтобы получить ее. Это потому, что вероятность выпадения четверки составляет 1/12.
Какова вероятность получить четверку раньше, чем двойку и тройку? Для начала давайте вспомним распространенное правило вероятности для случаев, когда A и B не являются взаимоисключающими:
пр(А или В) = пр(А) + пр(В) - пр(А и В)
Вы вычитаете pr(A и B), потому что эта случайная величина учитывается дважды в pr(A) + pr(B). Таким образом,
pr(4 перед 2 или 3) = pr(4 перед 2) + pr(4 перед 3) - pr(4 перед 2 и 3) = (3/4)+(3/5)-(3/6) = 0,85.
Вероятность того, что на пути к двойке и тройке не выпадет четверка, составляет 1,0 - 0,85 = 0,15. Таким образом, существует 15% вероятность того, что потребуется еще 12 бросков. Следовательно, ожидаемое количество бросков для получения двойки, тройки и четверки составляет 42 + 0,15 * 12 = 43,8.
Далее, подумайте, сколько еще бросков вам понадобится, чтобы получить пятерку. К тому моменту, когда вы выбросите от двойки до четырех, если пятерка еще не выпала, вам придется бросить кубики в среднем еще 9 раз, чтобы получить ее, потому что вероятность выпадения пятерки составляет 4/36 = 1/9.
Какова вероятность получить пятерку раньше, чем двойку, тройку или четверку? Общее правило таково:
pr (A или B или C) = pr(A) + pr(B) + pr(C) - pr(A и B) - pr(A и C) - pr(B и C) + pr(A и B и C)
Итак, pr(5 до 2, 3 или 4) = pr(5 до 2)+pr(5 до 3)+pr(5 до 4)-pr(5 до 2 и 3)-pr(5 до 2 и 4)-pr(5 до 3 и 4)+pr(5 до 2, 3 и 4) = (4/5)+(4/6)+(4/7)-(4/7)-(4/8)-(4/9)+(4/10) = 83/90. Вероятность не получить четверку на пути к двойке или четверке составляет 1 - 83/90 = 7/90. Таким образом, существует 7,78% вероятность того, что потребуется 7,2 дополнительных броска. Следовательно, ожидаемое количество бросков для получения двойки, тройки, четверки и пятерки составляет 43,8 + (7/90)*9 = 44,5.
Продолжайте следовать той же логике, доведя общее число до шести-двенадцати. Количество вычислений, необходимых для определения вероятности получения следующего числа до того, как оно выпадет, будет зависеть от того, насколько примерно удваивается каждое последнее число. К тому моменту, когда вы дойдете до двенадцати, вам придется выполнить 1023 вычисления.
Вот общее правило для pr(A или B или C или ... или Z)
pr(A или B или C или ... или Z) =
pr(A) + pr(B) + ... + pr(Z)
- pr (A и B) - pr (A и C) - ... - pr (Y и Z) Вычтите вероятность каждой комбинации двух событий
+ pr (A и B и C) + pr(A и B и D) + ... + pr(X и Y и Z) Сложите вероятности каждой комбинации из трех событий
- pr (A и B и C и D) - pr (A и B и C и E) - ... - pr (W и X и Y и Z) Вычтите вероятность каждой комбинации из четырех событийЗатем повторяйте эти действия, не забывая добавлять вероятности для нечетного числа событий и вычитать вероятности для четного числа событий. Очевидно, что при большом количестве возможных событий это становится утомительным, и на практике для этого требуется электронная таблица или компьютерная программа.
В следующей таблице показано ожидаемое количество бросков для каждого этапа. Например, 36 для получения двойки, 42 для получения двойки и тройки. В нижней правой ячейке указано ожидаемое количество бросков для получения всех 11 сумм, равное 61,217385.
Задача на определение ожидаемого количества рулонов
| Максимально необходимое количество | Вероятность | Ожидаемое количество рулонов при необходимости | Вероятность не требуется | Необходима вероятность | Ожидаемое общее количество бросков кубиков |
|---|---|---|---|---|---|
| 2 | 0.027778 | 36.0 | 0.000000 | 1.000000 | 36.000000 |
| 3 | 0.055556 | 18.0 | 0.666667 | 0.333333 | 42.000000 |
| 4 | 0.083333 | 12.0 | 0.850000 | 0.150000 | 43.800000 |
| 5 | 0.111111 | 9.0 | 0.922222 | 0.077778 | 44.500000 |
| 6 | 0.138889 | 7.2 | 0.956044 | 0.043956 | 44.816484 |
| 7 | 0.166667 | 6.0 | 0.973646 | 0.026354 | 44.974607 |
| 8 | 0.138889 | 7.2 | 0.962994 | 0.037006 | 45.241049 |
| 9 | 0.111111 | 9.0 | 0.944827 | 0.055173 | 45.737607 |
| 10 | 0.083333 | 12.0 | 0.911570 | 0.088430 | 46.798765 |
| 11 | 0.055556 | 18.0 | 0.843824 | 0.156176 | 49.609939 |
| 12 | 0.027778 | 36.0 | 0.677571 | 0.322429 | 61.217385 |
Этот вопрос был поднят и обсужден на форуме моего дочернего сайта Wizard of Vegas .
Согласно сайтуCraps Advantage Players , казино Лас-Вегаса регулярно используют утяжеленные игральные кости, чтобы увеличить соотношение выпадения семерок и, таким образом, повысить прибыль. Я в полном недоумении! Что по этому поводу скажет Волшебник?
Волшебник говорит, что этот сайт звучит как сплошная тирада и бред без каких-либо убедительных доказательств, подтверждающих обвинение. Я был бы рад разоблачить любое казино, использующее предвзятые игральные кости, если бы у меня были хоть какие-то доказательства.
Если у кого-либо есть достоверные доказательства предвзятости бросков кубиков, я с удовольствием изучу их и опубликую свои выводы. В качестве доказательств я хотел бы увидеть либо журналы бросков, либо, что еще лучше, реальные примеры предполагаемой предвзятости бросков кубиков.
Более того, если казино действительно использовали игральные кости, которые выдавали больше семерок, чем ожидалось, то почему эти детективы не осведомлены о заговоре, в рамках которого делались ставки на то, что выпадет неверный ход, и как они манипулировали коэффициентами?
Бонусный раунд Hot Roll на игровых автоматах награждает игрока следующим количеством монет в зависимости от суммы двух выпавших на кубиках чисел. Игрок продолжает получать выигрыш, пока не выбросит в сумме семь, после чего бонусный раунд завершается. Если при первом броске выпадает семерка, игрок получает утешительный приз в размере 70 монет. Ниже приведены призы за все остальные суммы, кроме семи:
- 2 или 12: 1000
- 3 или 11: 600
- 4 или 10: 400
- 5 или 9: 300
- 6 или 8: 200
Мой вопрос: каков средний выигрыш по бонусам?
Нажмите на следующую кнопку, чтобы увидеть ответ.
[спойлер]Ответ: 1983,33.[/spoiler]Нажмите на следующую кнопку, чтобы получить решение.
[спойлер] Пусть x — ответ. Пока игрок не выбросит семерку, он всегда может рассчитывать на то, что в будущем его выигрыш будет равен x, в дополнение ко всем предыдущим выигрышам. Другими словами, у бросания кубиков есть свойство отсутствия памяти: независимо от того, сколько бросков вы уже сделали, вы ни на шаг не приблизились к семерке, чем были в начале.Я не буду вдаваться в основы вероятностей, связанных с игральными костями, но скажу лишь, что вероятность каждой суммы выпадений следующая:
- 2: 1/36
- 3: 2/36
- 4: 3/36
- 5: 4/36
- 6: 5/36
- 7: 6/36
- 8: 5/36
- 9: 4/36
- 10: 3/36
- 11: 2/36
- 12: 1/36
Прежде чем рассматривать утешительный приз, значение x можно выразить следующим образом:
x = (1/36)*(1000 + x) + (2/36)*(600 + x) + (3/36)*(400 + x) + (4/36)*(300 + x) + (5/36)*(200 + x) + (5/36)*(200 + x) + (4/36)*(300 + x) + (3/36)*(400 + x) + (2/36)*(600 + x) + (1/36)*(1000 + x)Далее умножьте обе стороны на 36:
36x = (1000 + x) + 2*(600 + x) + 3*(400 + x) + 4*(300 + x) + 5*(200 + x) + 5*(200 + x) + 4*(300 + x) + 3*(400 + x) + 2*(600 + x) + (1000 + x)36x = 11200 + 30x
6x = 11 200
x = 11 200/6 = 1866,67.
Далее, размер утешительного приза составляет 700*(6/36) = 116,67.
Таким образом, средний выигрыш по бонусу составляет 1866,67 + 116,67 = 1983,33.
[/spoiler]


