Игры, не относящиеся к казино - Часто задаваемые вопросы
Мне нравится играть в покер «Лжецы» с долларовыми купюрами. Какова вероятность того, что на купюре выпадет любая цифра 1, 2, 3, 4 или 5? Спасибо. Если я играю втроем, какова вероятность того, что выпадет хотя бы одна цифра?
Сначала позвольте мне ответить на незаданный вопрос о вероятности того, что определённое число появится n раз на случайной купюре. На купюре 8 цифр, поэтому вероятность появления n определённого числа равна combin(8,n)*0.1 n *0.9 8-n /10 8 . Вот таблица, показывающая вероятность появления от 0 до 8 определённого числа.
Нечетность конкретных чисел в покере лжецов
| Число | Вероятность |
|---|---|
| 8 | 0.00000001 |
| 7 | 0.00000072 |
| 6 | 0.00002268 |
| 5 | 0.00040824 |
| 4 | 0.00459270 |
| 3 | 0.03306744 |
| 2 | 0.14880348 |
| 1 | 0.38263752 |
| 0 | 0.43046721 |
| Общий | 1.00000000 |
В следующей таблице показана вероятность каждого возможного типа купюр, сгруппированных по количеству каждого вида n одинаковых купюр. Например, для серийного номера 66847680 будет одна тройка одинаковых купюр, одна пара и три одиночные купюры, что соответствует вероятности 0,1693440.
Общие вероятности в игре "Покер лжецов"
| 8 дубов | 7 дубов | 6 дубов | 5 дубов | 4 дуба | 3 дуба | 2 дуба | 1 дуб | Вероятность |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.0000001 | |||||||
| 1 | 1 | 0.0000072 | ||||||
| 1 | 1 | 0.0000252 | ||||||
| 1 | 2 | 0.0002016 | ||||||
| 1 | 1 | 0.0000504 | ||||||
| 1 | 1 | 1 | 0.0012096 | |||||
| 1 | 3 | 0.0028224 | ||||||
| 2 | 0.0000315 | |||||||
| 1 | 1 | 1 | 0.0020160 | |||||
| 1 | 2 | 0.0015120 | ||||||
| 1 | 1 | 2 | 0.0211680 | |||||
| 1 | 4 | 0.0211680 | ||||||
| 2 | 1 | 0.0020160 | ||||||
| 2 | 2 | 0.0141120 | ||||||
| 1 | 2 | 1 | 0.0423360 | |||||
| 1 | 1 | 3 | 0.1693440 | |||||
| 1 | 5 | 0.0846720 | ||||||
| 4 | 0.0052920 | |||||||
| 3 | 2 | 0.1270080 | ||||||
| 2 | 4 | 0.3175200 | ||||||
| 1 | 6 | 0.1693440 | ||||||
| 8 | 0.0181440 | |||||||
| Общий | 1.0000000 | |||||||
дуб = "своего рода"
Для получения более подробной информации посетите мою страницу о покере лжецов .
Bank of America предлагает утроить сумму выбранного депозита, сделанного ежедневно в банкомате. Конкурс продлится около двух месяцев. Увеличатся ли мои шансы, если я внесу 300 долларов... сделать три депозита по 100 долларов или один депозит по 300 долларов... или мои общие шансы настолько низки, что разница не стоит затраченных усилий?
Ваш ожидаемый выигрыш одинаков независимо от того, сколько раз вы разделите общую сумму своих депозитов. Хорошая стратегия — вносить и выводить одни и те же деньги как можно чаще. Однако ваши шансы могут быть настолько низкими, что это не стоит усилий.
Вопрос по восточной игре в кости, где игроки должны угадать, какая сторона кубика выпадет. Сначала игроки делают ставки на 1, 2, 3, 4, 5, 6 (как в рулетке), а затем «дилер» одновременно бросает 3 кубика. Выплаты составляют 1:1, если выбранное число выпадает один раз (на любом из 3 кубиков), 2:1, если выбранное число выпадает дважды, и 3:1, если выбранное число выпадает на всех 3 кубиках. Поскольку игрок может сделать любое количество ставок на игровом поле, какое будет оптимальное количество ставок? (при условии, что все мои ставки равны по размеру)
Вероятность совпадения трех чисел составляет 1/216. Вероятность совпадения двух чисел составляет 3*5/216. Вероятность совпадения одного числа составляет 25*5/216. Вероятность отсутствия совпадений составляет 5*5*5/216. Таким образом, ожидаемая прибыль составляет 3*(1/216)+2*(15/216)+1*(75/216)-1*(125/216)=-17/216=-7,87%. Оптимального количества ставок не существует, вы потеряете ожидаемые 7,87% от общей суммы поставленных денег независимо от того, что вы делаете.
Эти ставки можно делать как в сик бо , так и в чак а лак .
Каковы шансы выиграть в стандартной партии пасьянса «Клондайк» в версии для Windows?
Это, пожалуй, самый часто задаваемый мне вопрос, на который у меня нет ответа. Полной версии пасьянса «Клондайк» до сих пор не существует. Возможно, когда компьютеры станут в миллион раз быстрее, кто-нибудь наконец-то это сделает. Однако ходят слухи, что казино Вегаса предлагали эту игру, по крайней мере, в пятидесятые годы. Я спрашивал об этом у нескольких завсегдатаев Вегаса, но пока никому это не удалось.
Недавно во время игры в нарды мне четыре раза подряд выпали две шестерки. Какова вероятность того, что это повторится?
При каждом новом броске вероятность того, что следующие четыре броска будут состоять из двух шестерок, составляет (1/36) 4 = 1 из 1679616.
Привет! На сайте www.transience.com.au/pearl.html есть игра под названием «Жемчуг для свиней». Жемчуг сгруппирован в три ряда (5+4+3), и в свой ход вы можете убрать столько жемчужин, сколько хотите, из одного ряда. Цель игры — оставить последнюю жемчужину для вашего противника. Игрок (я) всегда начинает (и всегда проигрывает). Почему я никогда не выигрываю? У моего противника есть хитрая система, позволяющая ему всегда побеждать, можете ли вы раскрыть его секрет?
Начните с удаления 2 жемчужин из ряда с 3, оставив 1+4+5. Независимо от того, что ваш противник сделает на следующем ходу, оставьте ему любой из следующих вариантов: 1+1+1, 1+2+3 или 4+4. Из любого из этих вариантов вынудите противника оказаться в ситуации, когда у него будет две стопки по 2 или более жемчужин в каждой, или нечетное количество стопок по 1 жемчужине в каждой.
Какой набор в игре «Монополия» лучший?
Мне больше всего нравится оранжевый набор. Он предлагает лучшую окупаемость инвестиций. Например, отель в оранжевом наборе стоит 500 долларов, а средняя арендная плата составляет 966,67 долларов, что дает соотношение арендной платы к расходам 1,93. Единственный набор с более высоким соотношением — светло-голубой, 2,27. Однако максимальная арендная плата в светло-голубом наборе составляет всего 600 долларов. Арендная плата за три дома в оранжевом наборе такая же, как и за отели в светло-голубом, но стоит на 20% меньше, и есть возможность построить больше. Кроме того, в оранжевом наборе очень удобно выпадать сразу после выхода из тюрьмы. Поэтому прислушайтесь к моему совету и при торговле старайтесь получить оранжевый набор.
Какой совет вы могли бы дать по игре в «камень/ножницы/бумага»?
Лучший совет на этом сайте, пожалуй, такой: в первом раунде ВСЕГДА ВЫБИРАЙТЕ БУМАГУ. Дело в том, что игроки-любители, как правило, в первый раз выбирают камень. Просто протяните руку в каждой позиции по очереди, и вы увидите, что камень — самый удобный и естественный выбор. Если вы играете несколько раундов подряд, выбирайте то, что с вероятностью менее одной трети обыграло бы вашего противника в предыдущем раунде. Это потому, что, как я считаю, любители повторяют ходы менее чем в одной трети случаев. Если вы играете против профессионала, который, как вы опасаетесь, может вывести вас из себя, то проведите случайный ход, посмотрев на секундную стрелку часов, разделите количество секунд на три и возьмите остаток, затем распределите ход следующим образом: 0 = камень, 1 = ножницы, 2 = бумага (или любое другое распределение, главное, чтобы оно было определено заранее). Так что в следующий раз, когда вы пойдете в ресторан по-голландски, я предлагаю сыграть один раунд на счет, а затем выбрать бумагу. Можете поблагодарить меня позже.
В игре Risk у кого преимущество, когда атакующий бросает три кубика, а защитник — два?
Для тех, кто не знаком с этой игрой, Risk — величайшая настольная игра всех времен. Те, кто в нее не играл, еще не жили. Чтобы ответить на ваш вопрос о типичной битве 3 против 2, возможны следующие исходы:
- Защитник проигрывает обоим: 37,17%
- Каждый теряет по одному: 33,58%
- Нападающий теряет оба варианта: 29,26%
В игре в Ятзи, если на карточке осталась только сама карта Ятзи, какова вероятность её получения?
В следующей таблице показана вероятность успеха при последнем броске в зависимости от количества дополнительных кубиков, необходимых для составления комбинации «Ятзи».
Вероятности последнего броска в Яхтзи
| Нужный | Вероятность успеха |
| 0 | 1 |
| 1 | 0.166667 |
| 2 | 0.027778 |
| 3 | 0,00463 |
| 4 | 0.000772 |
В следующей таблице показаны вероятности улучшения. В левом столбце указано, сколько кубиков нужно бросить до любого заданного броска, а в верхнем — сколько после броска. В основной части таблицы указана вероятность достижения заданной степени улучшения.
Вероятности улучшения
| Необходимо перед броском | 0 | 1 | 2 | 3 | 4 | Общий |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0.166667 | 0.833333 | 0 | 0 | 0 | 1 |
| 2 | 0.027778 | 0.277778 | 0.694444 | 0 | 0 | 1 |
| 3 | 0,00463 | 0.069444 | 0.37037 | 0.555556 | 0 | 1 |
| 4 | 0.000772 | 0.01929 | 0.192901 | 0.694444 | 0.092593 | 1 |
В следующей таблице показана вероятность того, что при первом броске потребуется от 0 до 4 дополнительных кубиков, чтобы составить Ятзи.
Вероятности первого броска в игре Яхтзи
| Нужный | Вероятность |
| 0 | 0.000772 |
| 1 | 0.019290 |
| 2 | 0.192901 |
| 3 | 0.694444 |
| 4 | 0.092593 |
В следующей таблице показана вероятность улучшения, а затем и окончательного успеха в зависимости от количества кубиков, необходимых после первого броска. Например, если игроку нужно еще 3 кубика, чтобы получить «Ятзи», вероятность улучшения до необходимости получить еще 2 кубика после второго броска и получения «Ятзи» на третьем броске составляет 0,010288066.
Вероятности выигрыша в Яхтзи после первого броска в зависимости от количества необходимых бросков до и после второго.
| Необходимо перед броском | 0 | 1 | 2 | 3 | 4 | Общий |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0.166667 | 0.138889 | 0 | 0 | 0 | 0.305556 |
| 2 | 0.027778 | 0.046296 | 0.01929 | 0 | 0 | 0.093364 |
| 3 | 0,00463 | 0.011574 | 0.010288 | 0.002572 | 0 | 0.029064 |
| 4 | 0.000772 | 0.003215 | 0.005358 | 0.003215 | 0.000071 | 0.012631 |
Чтобы получить окончательный ответ, возьмите скалярное произведение числа, необходимого после первого броска двух таблиц вверх, и вероятности успеха в последнем столбце одной таблицы вверх. Это 0,092593*0,012631 + 0,694444*0,029064 + 0,192901*0,093364 + 0,019290*0,305556 + 0,000772*1 = 4,6028643%. Для подтверждения этого я провел симуляцию игры на 100 000 000 игр, и смоделированная вероятность составила 4,60562%.
Если в игре «камень/ножницы/бумага» в качестве варианта выбора предлагается динамит, и динамит побеждает камень и бумагу, но ножницы побеждают динамит, то какой должна быть оптимальная стратегия, если играют два безупречных логика?
Во-первых, можно исключить игру в бумагу. Независимо от того, что бросит другой игрок, вы получите равный или даже больший выигрыш, бросив динамит поверх бумаги. Как только бумага исключена, динамит, по сути, становится новой бумагой, побеждая камень и проигрывая ножницам. Поэтому идеальная стратегия — выбирать случайным образом и с равной вероятностью между камнем, ножницами и динамитом.
Какова наилучшая стратегия в одной из тех будок, где деньги разлетаются во все стороны, и нужно собрать как можно больше за ограниченное время?
Я задал этот вопрос Рэнди Хиллу из компании Fun Industries Inc. Он сказал, что нужно вытянуть руки прямо, ладонями вниз, и позволить деньгам взлететь и удариться о дно ладоней и предплечий. Когда накопится достаточно денег, нужно просунуть их через щель.
Предположим, у нас есть азартная игра. Монета без форы подбрасывается несколько раз. За каждый бросок мы должны заплатить 1 рупию. Возможны два исхода: H или T. Если разница между выпадением орла и решки равна 3, мы получим от игрока 8 рупий. Стоит ли нам играть в эту игру и почему? Какова наша вероятность выигрыша? Как повлияет на вероятность выигрыша получение 7 или 9 рупий?
Назовем x ожидаемым числом бросков относительно начальной точки.
Назовем y ожидаемым числом оставшихся бросков, если одна из сторон выигрывает один раз из большинства.
Назовем z ожидаемым числом оставшихся бросков, если одна сторона имеет преимущество в два броска в большинстве.
E(x) = 1 + E(y)
E(y) = 1 + 0,5*E(x) + 0,5*E(z)
E(z) = 1 + 0,5*E(y)
Затем, с помощью матричных алгебраических вычислений, легко увидеть, что E(x) = 9, E(y) = 8 и E(z) = 5. Таким образом, в среднем потребуется 9 бросков, чтобы разница между орлом и решкой составила 3. Поэтому ставка в 8 рупий является выгодной для игрока, получающего одну рупию за бросок, поскольку в среднем он получит 9 рупий, но вернет только 8. Преимущество казино для игрока составляет 11,11%. При ставке в 9 рупий это справедливая ставка, при 7 рупиях преимущество казино составляет 22,22%.
В своей колонке от 28 ноября 2002 года вы рассмотрели правильную стратегию для игры Pearls Before Swine . У них также есть продолжение под названием Pearls Before Swine II . Как пройти эту версию?
В колонке от 28.11.02 я объясняю, как играть, когда осталось всего три ряда. Вот моя стратегия для четырех рядов. Когда наступит ваша очередь, посмотрите конфигурацию в левой колонке и разыграйте то, что указано в правой колонке. Например, начальная позиция 3456 указана последней и показывает, что вам следует убрать 4 жемчужины из ряда с 5, оставив 1346. Если в левой колонке написано «Проиграть», то выиграть невозможно, если противник использует оптимальную стратегию, что, кажется, всегда происходит в игре на Transcience.
В этой таблице прослеживается закономерность: нужно заставить противника оказаться в ситуации, когда сумма жемчужин в ряду с наименьшим и наибольшим количеством жемчужин равна сумме двух рядов с наибольшим количеством жемчужин в середине. Это включает в себя оставление нуля в ряду с наименьшим количеством жемчужин.
Стратегия Pearls Before Swine II
| У вас есть | Оставлять |
| 1111 | 111 |
| 1112 | 111 |
| 1113 | 111 |
| 1114 | 111 |
| 1115 | 111 |
| 1116 | 111 |
| 1122 | Терять |
| 1123 | 1122 |
| 1124 | 1122 |
| 1125 | 1122 |
| 1126 | 1122 |
| 1133 | Терять |
| 1134 | 1133 |
| 1135 | 1133 |
| 1136 | 1133 |
| 1144 | Терять |
| 1145 | 1144 |
| 1146 | 1144 |
| 1155 | Терять |
| 1156 | 1155 |
| 1222 | 1122 |
| 1223 | 1122 |
| 1224 | 1122 |
| 1225 | 1122 |
| 1226 | 1122 |
| 1233 | 123 |
| 1234 | 123 |
| 1235 | 123 |
| 1236 | 123 |
| 1244 | 1144 |
| 1245 | 145 |
| 1246 | 246 |
| 1255 | 1155 |
| 1256 | Терять |
| 1333 | 1133 |
| 1334 | 1133 |
| 1335 | 1133 |
| 1336 | 1133 |
| 1344 | 1144 |
| 1345 | 145 |
| 1346 | Терять |
| 1355 | 1155 |
| 1356 | 1256 |
| 1444 | 1144 |
| 1445 | 1144 |
| 1446 | 1144 |
| 1455 | 1155 |
| 1456 | 1346 |
| 2222 | Терять |
| 2223 | 2222 |
| 2224 | 2222 |
| 2225 | 2222 |
| 2226 | 2222 |
| 2233 | Терять |
| 2234 | 2233 |
| 2235 | 2233 |
| 2236 | 2233 |
| 2244 | Терять |
| 2245 | 2244 |
| 2246 | 2244 |
| 2255 | Терять |
| 2256 | 2255 |
| 2333 | 2233 |
| 2334 | 2233 |
| 2335 | 2233 |
| 2336 | 2233 |
| 2344 | 2244 |
| 2345 | Терять |
| 2346 | 1346 |
| 2355 | 2255 |
| 2356 | 2345 |
| 2444 | 2244 |
| 2445 | 2244 |
| 2446 | 2244 |
| 2455 | 2255 |
| 2456 | 2345 |
| 3333 | Терять |
| 3334 | 3333 |
| 3335 | 3333 |
| 3335 | 3333 |
| 3336 | 3333 |
| 3344 | Терять |
| 3345 | 3344 |
| 3346 | 3344 |
| 3355 | Терять |
| 3356 | 3355 |
| 3444 | 3344 |
| 3445 | 3344 |
| 3446 | 3344 |
| 3455 | 3355 |
| 3456 | 1346 |
Брэд С. предложил добавить общую стратегию для любого количества жемчужин и рядов. Сначала нужно разбить каждый ряд на его бинарные компоненты. Например, начальная позиция в игре Transcience будет следующей.
- 3 = 2+1
- 4 = 4
- 5 = 4+1
- 6 = 4+2
Затем вы стараетесь оставить четное количество чисел, являющихся степенями двойки. Например, в приведенном выше примере есть две единицы, две двойки и три четверки. Таким образом, появляется лишняя четверка. Затем вы удаляете 4 из любой строки, содержащей число 4. Продолжайте делать это, пока не сможете уменьшить количество единиц до 2, 2 или нечетного числа единиц.
Попробуйте эту стратегию в игре Pearl 3 , вы всегда будете выигрывать. Если вы начинаете с проигрышной ситуации, как это было у меня в 10-й игре (4+7+8+11), вы можете нажать кнопку «старт», чтобы он начал первым.
Я не покупаю вашу игру NIM ! Я всегда думал, что ключ к победе — это оставить противнику (в данном случае, компьютеру) точки, сумма которых равна следующему наименьшему числу, равному его двоичной сумме, то есть, если у меня 17 точек, я забираю 2 и оставляю 15, сумму двоичных чисел 1, 2, 4, 8. Но это, похоже, не работает. Я прав или нет?
Вы на верном пути с двоичными числами, но это не совсем выигрышная стратегия. Во-первых, если вы можете оставить противнику нечётное количество строк по одному числу в каждой, сделайте это. В противном случае разбейте каждую строку на её двоичные компоненты. Например, 99 будет 64+32+2+1. Затем сложите количество каждого компонента по всем строкам. Затем найдите ход, который оставит противнику чётное количество всех двоичных компонентов по всем строкам.
Рассмотрим пример. Предположим, настала ваша очередь, и ситуация выглядит следующим образом.
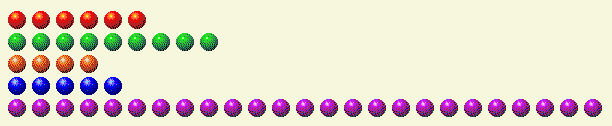
В следующей таблице каждая строка разбита на двоичные компоненты.
Ход игрока 1
| Ряд | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 25 | 1 | 0 | 0 | 1 | 1 |
| Общий | 3 | 1 | 3 | 2 | 1 |
Как видите, количество единиц, двоек, четверок и шестнадцаток нечетное. Очевидно, нам нужно уменьшить число 25 в ряду до 16, чтобы исключить 16-ю единицу. Чтобы сумма двоичных компонентов оставалась четной, нам нужно убрать 1, добавить 2, добавить 4, оставить 8 и убрать 16. Это означает, что лучший ход — 2+4+8=14 в последнем ряду. Оставив 14 в нижнем ряду, мы получаем следующее.
Первый ход компьютера
| Ряд | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 14 | 0 | 1 | 1 | 1 | 0 |
| Общий | 2 | 2 | 4 | 2 | 0 |
Затем очередь переходит к компьютеру, и в итоге мы получаем вот это.
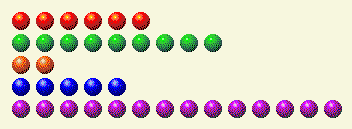
Вот бинарное разложение этого понятия.
Ход игрока 2
| Ряд | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 14 | 0 | 1 | 1 | 1 | 0 |
| Общий | 2 | 3 | 3 | 2 | 0 |
Здесь нам нужно убрать 2 и 4, чтобы получить равные суммы. Есть только одна строка, 14, в которой присутствуют оба компонента. Поэтому уберем из нее 6, останется 8.
Второй ход компьютера
| Ряд | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 0 |
| Общий | 2 | 2 | 2 | 2 | 0 |
Затем очередь переходит к компьютеру, и в итоге мы получаем вот это.
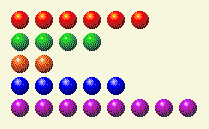
Теперь нам нужно поменять местами столбцы 1, 4 и 8.
Ход игрока 3
| Ряд | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 0 |
| Общий | 1 | 2 | 3 | 1 | 0 |
Это можно сделать, изменив строку с 8 на 5 следующим образом.
Третий ход компьютера
| Ряд | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| Общий | 2 | 2 | 4 | 0 | 0 |
Затем очередь переходит к компьютеру, и в итоге мы получаем вот это.
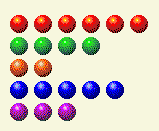
Теперь нам нужно поменять местами суммы 2 и 4.
Ход игрока 4
| Ряд | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| Общий | 2 | 3 | 3 | 0 | 0 |
Это можно сделать, заменив 6 на 0.
Четвёртый ход компьютера
| Ряд | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| Общий | 2 | 2 | 2 | 0 | 0 |
Затем очередь переходит к компьютеру, и в итоге мы получаем вот это.
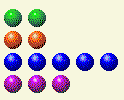
Теперь нам нужно поменять местами двойки и четверки.
Ход игрока 5
| Ряд | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| Общий | 2 | 3 | 1 | 0 | 0 |
Этого можно добиться, изменив ряд из 5 чисел на 3. Если вам удастся привести противника к ситуации x, x, y, y, вы обязательно выиграете, если сможете поддерживать эту ситуацию до конца.
Поворот компьютера 5
| Ряд | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| Общий | 2 | 4 | 0 | 0 | 0 |
В следующих нескольких ходах я заставляю компьютер использовать последовательность x, x, y, y. В этот раз компьютер оставляет мне 2, 2, 3, 2; поэтому я оставляю ему 2, 2, 2, 2.

Затем компьютер выдает мне 2,2,1,2. Я оставляю ему 2,2,1,1.
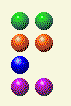
Компьютер оставляет мне 2, 2, 1. Я оставляю ему 2, 2. Если вам удастся выстроить два одинаковых ряда против вашего противника, вы обязательно выиграете, главное — чтобы ряды были одинаковыми.

Затем компьютер оставляет мне одну кучу из 2 штук, и я убираю 1.

Игра подошла к концу.
Недавно я приобрел карнавальное колесо, принадлежавшее моему двоюродному деду. Ему около ста лет, и я пытаюсь разработать игру на его основе. На нем случайным образом выпадают числа от 1 до 60, чередуются черные и красные, а каждые пятнадцатые деления отмечены зеленой звездочкой. Не могли бы вы помочь мне определить размер выигрыша за каждое вращение?
Итак, есть 30 черных, 30 красных и 4 зеленых числа. Это означает, что вероятность выпадения черного числа составляет 30/64, красного — 30/64, а зеленого — 4/64. Если вероятность события равна p, то справедливые шансы равны (1-p)/p к 1. Таким образом, справедливые шансы для любого красного числа будут (34/64)/(30/64) = 34 к 30 = 17 к 15. То же самое для черного. Справедливые шансы для зеленого числа равны (60/64)/(4/64) = 60 к 4 = 15 к 1. Для конкретного числа справедливые шансы равны (63/64)/(1/64) = 63 к 1.
Я предлагаю делать ставки 1 к 1 на красное и чёрное, 14 к 1 на зелёное и 60 к 1 на любой отдельный номер. Одна из формул для расчета преимущества казино — (ta)/(t+1), где t — истинные шансы, а a — фактические шансы. В данном случае преимущество казино на ставку на красное или чёрное составляет (63-60)/(63+1) = 3/64 = 4,69%. На ставку на зелёное преимущество казино составляет (15-14)/(15+1) = 1/16 = 6,25%. На отдельные номера преимущество казино составляет (63-60)/(63+1) = 3/64 = 4,69%.
В штате Нью-Йорк в пунктах приема ставок вне ипподромов установлены видеолотерейные терминалы (VLT). Термин «автомат приближается к своей «установленной точке»» используется, когда он «работает на полную мощность» и раздает выигрышные комбинации одну за другой. Это объясняет, почему один и тот же автомат выплачивает выигрыши в один день, а в другие дни работает нестабильно. Кроме того, большинство таких автоматов не позволяют проиграть выигрышную комбинацию. Просто выбросьте её, и автомат вернет вам эквивалентную или даже лучшую комбинацию. Что вы думаете по этому поводу?
Виртуальные лотерейные автоматы (VLT) — это, по сути, игры с отрывными карточками. Существует заранее определённый пул исходов. Когда вы играете, игра случайным образом выбирает один из исходов из пула и отображает выигрыш игроку в виде игрового автомата или видеопокера. Поскольку исход предопределён, любой элемент мастерства является воображаемым. Например, если вам выпал роял-флеш, и вы его выбросили, вы получите ещё один при раздаче. Обычно я говорю, что в азартных играх прошлое не имеет значения, но в данном случае есть эффект исключения. Если вы сыграли один раз и проиграли, то это незначительно улучшит шансы на выигрыш в оставшихся играх, пока не закончится запас виртуальных отрывных карточек, и, я полагаю, виртуальный барабан не будет пополнен. Я считаю, что ваши колебания — это просто обычная удача, а любая предопределённость — воображаемая.
Позже один из читателей добавил к этой теме следующее.
У меня есть комментарий к вашей колонке «Спроси волшебника» от 14 февраля (№ 183). Он не имеет прямого отношения к вашему вопросу. Просто вам это может показаться интересным.
До принятия Предложения 1A, разрешившего полноценные игровые автоматы 3-го класса, у нас в течение нескольких лет работала небольшая установка типа VLT (виртуальных лотерейных терминалов). В нашей системе, которой управляла компания SDG (теперь часть Bally), призовой фонд изначально составлял 4 миллиона розыгрышей. Когда фонд уменьшился и осталось 2 миллиона, был добавлен следующий фонд в 4 миллиона, в результате чего общий фонд составил 6 миллионов розыгрышей. Когда фонд снова уменьшился до 2 миллионов, процесс повторился.
Какое количество бросков кубиков потребуется, чтобы получить Ятзи?
Если предположить, что игрок всегда вытягивает наиболее часто встречающееся число, то среднее значение составляет 11,09. Ниже приведена таблица, показывающая распределение количества бросков в ходе случайной симуляции, включающей 82,6 миллиона испытаний.
Эксперимент «Яхтзи»
| Роллы | События | Вероятность |
| 1 | 63908 | 0.00077371 |
| 2 | 977954 | 0.0118396 |
| 3 | 2758635 | 0.0333975 |
| 4 | 4504806 | 0.0545376 |
| 5 | 5776444 | 0.0699327 |
| 6 | 6491538 | 0.0785901 |
| 7 | 6727992 | 0.0814527 |
| 8 | 6601612 | 0.0799227 |
| 9 | 6246388 | 0.0756221 |
| 10 | 5741778 | 0.0695131 |
| 11 | 5174553 | 0.0626459 |
| 12 | 4591986 | 0.0555931 |
| 13 | 4022755 | 0.0487016 |
| 14 | 3492745 | 0.042285 |
| 15 | 3008766 | 0.0364257 |
| 16 | 2577969 | 0.0312103 |
| 17 | 2193272 | 0.0265529 |
| 18 | 1864107 | 0.0225679 |
| 19 | 1575763 | 0.019077 |
| 20 | 1329971 | 0.0161013 |
| 21 | 1118788 | 0.0135446 |
| 22 | 940519 | 0.0113864 |
| 23 | 791107 | 0.00957757 |
| 24 | 661672 | 0.00801056 |
| 25 | 554937 | 0.00671837 |
| 26 | 463901 | 0.00561624 |
| 27 | 387339 | 0.00468933 |
| 28 | 324079 | 0.00392347 |
| 29 | 271321 | 0.00328476 |
| 30 | 225978 | 0.00273581 |
| 31 | 189012 | 0.00228828 |
| 32 | 157709 | 0.00190931 |
| 33 | 131845 | 0.00159619 |
| 34 | 109592 | 0.00132678 |
| 35 | 91327 | 0.00110565 |
| 36 | 76216 | 0.00092271 |
| 37 | 63433 | 0.00076795 |
| 38 | 52786 | 0.00063906 |
| 39 | 44122 | 0.00053417 |
| 40 | 36785 | 0.00044534 |
| 41 | 30834 | 0.00037329 |
| 42 | 25494 | 0.00030864 |
| 43 | 21170 | 0.0002563 |
| 44 | 17767 | 0.0002151 |
| 45 | 14657 | 0.00017745 |
| 46 | 12410 | 0.00015024 |
| 47 | 10299 | 0.00012469 |
| 48 | 8666 | 0.00010492 |
| 49 | 7355 | 0.00008904 |
| 50 | 5901 | 0.00007144 |
| 51 | 5017 | 0.00006074 |
| 52 | 4227 | 0.00005117 |
| 53 | 3452 | 0.00004179 |
| 54 | 2888 | 0.00003496 |
| 55 | 2470 | 0.0000299 |
| 56 | 2012 | 0.00002436 |
| 57 | 1626 | 0.00001969 |
| 58 | 1391 | 0.00001684 |
| 59 | 1135 | 0.00001374 |
| 60 | 924 | 0.00001119 |
| 61 | 840 | 0.00001017 |
| 62 | 694 | 0.0000084 |
| 63 | 534 | 0.00000646 |
| 64 | 498 | 0.00000603 |
| 65 | 372 | 0.0000045 |
| 66 | 316 | 0.00000383 |
| 67 | 286 | 0.00000346 |
| 68 | 224 | 0.00000271 |
| 69 | 197 | 0.00000238 |
| 70 | 160 | 0.00000194 |
| 71 | 125 | 0.00000151 |
| 72 | 86 | 0.00000104 |
| 73 | 79 | 0.00000096 |
| 74 | 94 | 0.00000114 |
| 75 | 70 | 0.00000085 |
| 76 | 64 | 0.00000077 |
| 77 | 38 | 0.00000046 |
| 78 | 42 | 0.00000051 |
| 79 | 27 | 0.00000033 |
| 80 | 33 | 0.0000004 |
| 81 | 16 | 0.00000019 |
| 82 | 18 | 0.00000022 |
| 83 | 19 | 0.00000023 |
| 84 | 14 | 0.00000017 |
| 85 | 6 | 0.00000007 |
| 86 | 4 | 0.00000005 |
| 87 | 9 | 0.00000011 |
| 88 | 4 | 0.00000005 |
| 89 | 5 | 0.00000006 |
| 90 | 5 | 0.00000006 |
| 91 | 1 | 0.00000001 |
| 92 | 6 | 0.00000007 |
| 93 | 1 | 0.00000001 |
| 94 | 3 | 0.00000004 |
| 95 | 1 | 0.00000001 |
| 96 | 1 | 0.00000001 |
| 97 | 2 | 0.00000002 |
| 102 | 1 | 0.00000001 |
| Общий | 82600000 | 1 |
Знаете ли вы какой-нибудь сайт с хорошим анализом вероятностей/статистики/вероятностей в нардах, и можете ли вы порекомендовать какие-нибудь книги по любому аспекту этой игры?
Нарды — одна из моих любимых азартных игр. Я не пишу о них, потому что анализ игр между игроками крайне сложен. К тому же, я никак не могу найти в этой игре ничего принципиально нового. Поэтому я оставлю советы другим. Вот мои рекомендуемые ресурсы:
Нарды Пола Магриэля: Если бы существовала Библия нардов, это была бы она. Я горжусь тем, что являюсь обладателем старого издания в твердом переплете. Эта книга станет отличным началом. Хотя она была написана в 1976 году, советы по-прежнему актуальны.
«501 основная задача по нардам» Билла Роберти: Я пытаюсь осилить эту книгу уже много лет, и до сих пор прошел только половину пути. Удручает, что я допускаю ошибки в половине задач, и это заставляет меня думать, что я играю в нарды так же плохо, как и в гольф. Однако каждая ошибка – это ценный урок. Для игроков среднего и продвинутого уровня эта книга станет ценным и поучительным инструментом.
Программа для игры в нарды Snowie : я играю около 1000 партий в год против этой программы. Snowie не только играет практически идеально, но и точно показывает, насколько дорогостоящими могут быть ваши ошибки, когда вы их совершаете. Есть много других функций, которые я никогда не изучал. Если я чему-то и научился у Snowie, так это тому, что самая большая проблема в моей игре — это глупые ошибки, когда я иногда не замечаю совершенно очевидных ходов. Как и в шахматах, один плохой ход может перечеркнуть 100 хороших.
Сайт Motif : До покупки Snowie я сыграл бесчисленное количество партий против Motif. Стратегия, используемая Motif, на мой взгляд, очень надежна. Нет ничего лучше, чем играть против более сильного соперника, чтобы улучшить свою собственную игру.
В колонке от 11 апреля 2004 года есть вопрос о правильной стратегии в игре Price is Right Showcase Showdown . Предполагая, что используется оптимальная стратегия, какова вероятность победы каждого игрока?
В следующей таблице показана вероятность выигрыша каждого игрока в зависимости от первого вращения барабанов, где игрок 1 ходит первым, за ним следует игрок 2, а игрок 3 — последним. В нижней строке показаны общие вероятности выигрыша до первого вращения барабанов.
Вероятности в соревновании участников телеигры «Цена правильная»
| Вращение 1 | Стратегия | Игрок 1 | Игрок 2 | Игрок 3 |
| 0,05 | вращаться | 20,59% | 37,55% | 41,85% |
| 0.10 | вращаться | 20,59% | 37,55% | 41,86% |
| 0,15 | вращаться | 20,57% | 37,55% | 41,87% |
| 0.20 | вращаться | 20,55% | 37,55% | 41,9% |
| 0,25 | вращаться | 20,5% | 37,56% | 41,94% |
| 0.30 | вращаться | 20,43% | 37,56% | 42,01% |
| 0,35 | вращаться | 20,33% | 37,58% | 42,10% |
| 0,40 | вращаться | 20,18% | 37,60% | 42,22% |
| 0,45 | вращаться | 19,97% | 37,64% | 42,39% |
| 0,50 | вращаться | 19,68% | 37,71% | 42,61% |
| 0,55 | вращаться | 19,26% | 37,81% | 42,93% |
| 0,60 | вращаться | 18,67% | 37,96% | 43,36% |
| 0,65 | вращаться | 17,86% | 38,21% | 43,93% |
| 0,70 | оставаться | 21,56% | 38,28% | 40,16% |
| 0,75 | оставаться | 28,42% | 35,21% | 36,38% |
| 0,80 | оставаться | 36,82% | 31,26% | 31,92% |
| 0,85 | оставаться | 46,99% | 26,35% | 26,66% |
| 0,90 | оставаться | 59,17% | 20,36% | 20,47% |
| 0,95 | оставаться | 73,61% | 13,19% | 13,21% |
| 1.00 | оставаться | 90,57% | 4,72% | 4,72% |
| Средний | 30,82% | 32,96% | 36,22% |
Вот выигрышные комбинации из 6× 20 возможных.
Игрок 1: 118 331 250Игрок 2: 126 566 457
Игрок 3: 139,102,293
Какова правильная стратегия для Эйси Дьюси в домашней покерной игре? Мы играем так: если третья карта совпадает с одной из первых двух, то ставка — ничья.
В правилах игры, где совпадение третьей карты означает ничью, шансы склоняются в вашу пользу, когда между первыми двумя картами разница составляет не менее шести рангов (шесть карт). В моей игре в округе Ориндж совпадение третьей карты приводило к двойному проигрышу. По этому правилу шансы равны при разнице в восемь карт. Если совпадение третьей карты приводит к проигрышу в 1 раз, то для того, чтобы шансы были в вашу пользу, вам нужна разница в семь карт.
В игре в покер с одной картой используется колода из трех карт: туз, двойка и тройка. Туз — младшая карта, тройка — старшая. Каждый из двух игроков вносит по 1 доллару в банк. Затем каждый игрок получает по одной карте. Порядок ставок предопределен, первым ходит игрок 1. Игрок 1 может либо поставить 1 доллар, либо сделать чек. Если игрок 1 делает ставку, игрок 2 может либо ответить коллом, либо сбросить карты. Если игрок 1 делает чек, то игрок 2 может либо поставить 1 доллар, либо сделать чек. Если игрок 1 делает чек, и игрок 2 делает ставку, то игрок 1 может либо ответить коллом, либо сбросить карты. Если оба игрока делают чек или оба делают ставку, то банк выигрывает игрок с более старшей картой. Предполагая, что оба игрока — идеальные логики, какова оптимальная стратегия для каждого игрока?
Надеюсь, вы довольны; я потратил на это весь день. Ответ и решение можно найти на моем другом сайте mathproblems.info , задача 203, или в научной статье Джейсона Свонсона «Теория игр и покер» .
Я выбираю ипотеку в разных компаниях. Одна предлагает процентную ставку 5,75% плюс один пункт по 30-летней фиксированной ставке. Другая — 5,875% без пункта. Какое предложение выгоднее?
Для удобства других читателей поясню: пункт — это комиссия, взимаемая за кредит. Например, при кредите в 250 000 долларов один пункт будет равен 2500 долларам. Я предполагаю, что заемщик будет добавлять этот пункт к основной сумме долга и никогда не будет погашать основную сумму досрочно.
В следующей таблице показана эквивалентная процентная ставка без учета процентной ставки, в зависимости от процентной ставки с учетом процентной ставки и срока.
Эквивалентная процентная ставка без комиссионных сборов.
| Процентная ставка с One Point | 10 лет | 15 лет | 20 лет | 30 лет | 40 лет |
| 4,00% | 4,212% | 4,147% | 4,115% | 4,083% | 4,067% |
| 4,25% | 4,463% | 4,398% | 4,366% | 4,334% | 4,318% |
| 4,50% | 4,714% | 4,649% | 4,617% | 4,585% | 4,570% |
| 4,75% | 4,965% | 4,900% | 4,868% | 4,836% | 4,821% |
| 5,00% | 5,216% | 5,151% | 5,119% | 5,088% | 5,073% |
| 5,25% | 5,467% | 5,402% | 5,370% | 5,339% | 5,324% |
| 5,50% | 5,718% | 5,654% | 5,621% | 5,590% | 5,576% |
| 5,75% | 5,969% | 5,905% | 5,873% | 5,842% | 5,827% |
| 6,00% | 6,220% | 6,156% | 6,124% | 6,093% | 6,079% |
| 6,25% | 6,471% | 6,407% | 6,375% | 6,344% | 6,330% |
| 6,50% | 6,723% | 6,658% | 6,626% | 6,596% | 6,582% |
| 6,75% | 6,974% | 6,909% | 6,878% | 6,847% | 6,834% |
| 7,00% | 7,225% | 7,160% | 7,129% | 7,099% | 7,085% |
| 7,25% | 7,476% | 7,412% | 7,380% | 7,350% | 7,337% |
| 7,50% | 7,727% | 7,663% | 7,631% | 7,602% | 7,589% |
| 7,75% | 7,978% | 7,914% | 7,883% | 7,853% | 7,841% |
| 8,00% | 8,229% | 8,165% | 8,134% | 8,105% | 8,093% |
| 8,25% | 8,480% | 8,416% | 8,385% | 8,357% | 8,344% |
| 8,50% | 8,731% | 8,668% | 8,637% | 8,608% | 8,596% |
| 8,75% | 8,982% | 8,919% | 8,888% | 8,860% | 8,848% |
| 9,00% | 9,233% | 9,170% | 9,140% | 9,112% | 9.100% |
| 9,25% | 9,485% | 9,421% | 9,391% | 9,363% | 9,352% |
| 9,50% | 9,736% | 9,673% | 9,642% | 9,615% | 9,604% |
| 9,75% | 9,987% | 9,924% | 9,894% | 9,867% | 9,856% |
| 10,00% | 10,238% | 10,175% | 10,145% | 10,119% | 10,108% |
Это показывает, что процентная ставка 5,75% с одним пунктом эквивалентна 5,842% без пунктов. Другими словами, платеж будет одинаковым в обоих случаях, если предположить, что начисленный пункт добавляется к основной сумме долга. Ваше другое предложение составляло 5,875% без пунктов, что выше, чем 5,842%, поэтому я бы выбрал 5,75% с пунктом.
P.S. Для тех, кому интересно, как я вычислил i, я использовал функцию rate в Excel.
Мой сын за две недели дважды сделал хоул-ин-ван. Какова вероятность такого совпадения? У моего сына гандикап 1. Первый удар был на 151 ярд, а второй — на 137 ярдов, на двух разных полях.
Согласно книге Грегори Баера «Жизнь: шансы (и как их улучшить)» , вероятность попадания в лунку с первого удара на лунке пар-3 в турнирах PGA составляет 1 к 2491. Я считаю, что эти расстояния соответствуют лункам пар-3.
Гандикап 1 – это очень хороший результат, поэтому я не буду делать большой скидки по сравнению с игроками PGA Tour. Допустим, вероятность попадания вашего сына на лунку пар-3 составляет 1 к 3000. На типичном поле для гольфа около четырех лунок пар-3. Допустим, ваш сын играет каждый день. Это будет 28 лунок пар-3 в неделю. Вероятность сделать ровно два попадания в лунку с одного удара составит (28,2)×(1/3000) ² ×(2999/3000) ²⁶ = 1 к 24017.
Недавно я участвовал в лотерее, где разыгрывается 7033 приза, и, как говорят, шансы на выигрыш составляют 1 к 13. Я купил 5 билетов. Каковы мои реальные шансы на выигрыш? Кроме того, есть 40 крупных призов. Каковы мои шансы на выигрыш крупного приза?
Для простоты давайте не будем учитывать тот факт, что чем больше билетов вы покупаете, тем ниже становится стоимость каждого билета, потому что вы соревнуетесь сами с собой. При этом вероятность проиграть все пять билетов составляет (12/13) 5 = 67,02%. Таким образом, вероятность выиграть хотя бы один приз составляет 32,98%. В барабане до покупки находится 7033×13=91429 билетов. 91429-40=91389 — это не крупные призы. Вероятность не выиграть ни одного крупного приза с пятью билетами составляет (91389/91429) 5 = 99,78%. Таким образом, вероятность выиграть хотя бы один крупный приз составляет 0,22%, или 1 к 458.
В игре в червы каждому игроку раздают по 13 карт. Масть, в которой больше всего карт из 13, называется «длинной мастью», и в ней может быть от 4 до 13 карт. Какова вероятность каждой из этих сумм?
Вероятности выпадения длинной масти в червах
| Карты | Комбинации | Вероятность |
| 4 | 222766089260 | 0.35080524800183 |
| 5 | 281562853572 | 0.44339660045899 |
| 6 | 105080049360 | 0.16547685914958 |
| 7 | 22394644272 | 0.03526640326564 |
| 8 | 2963997036 | 0.00466761219692 |
| 9 | 235237860 | 0.00037044541245 |
| 10 | 10455016 | 0.00001646424055 |
| 11 | 231192 | 0.00000036407412 |
| 12 | 2028 | 0.00000000319363 |
| 13 | 4 | 0.00000000000630 |
| Общий | 635013559600 | 1 |
Правило 72 гласит, что если разделить годовую доходность на 72, то получится количество лет, за которое ваши деньги удвоятся. Например, инвестиции, приносящие 10% годовых, удвоятся за 72/10 = 7,2 года. Мой несколько праздный вопрос: почему именно 72?
Во-первых, «правило 72» — это приблизительное значение времени, необходимого для удвоения ваших денег, а не точный ответ. В следующей таблице показаны значения «правила 72» и точное количество лет для различных годовых процентных ставок.
Правило 72 — лет, чтобы удвоить деньги
| Процентная ставка | Правило 72 | Точный | Разница |
|---|---|---|---|
| 0,01 | 72.00 | 69.66 | 2.34 |
| 0,02 | 36.00 | 35.00 | 1.00 |
| 0,03 | 24.00 | 23.45 | 0,55 |
| 0,04 | 18.00 | 17.67 | 0,33 |
| 0,05 | 14.40 | 14.21 | 0,19 |
| 0,06 | 12.00 | 11.90 | 0.10 |
| 0,07 | 10.29 | 10.24 | 0,04 |
| 0,08 | 9.00 | 9.01 | -0.01 |
| 0,09 | 8.00 | 8.04 | -0.04 |
| 0.10 | 7.20 | 7.27 | -0.07 |
| 0.11 | 6.55 | 6.64 | -0.10 |
| 0,12 | 6.00 | 6.12 | -0.12 |
| 0,13 | 5.54 | 5.67 | -0.13 |
| 0,14 | 5.14 | 5.29 | -0.15 |
| 0,15 | 4.80 | 4.96 | -0.16 |
| 0,16 | 4.50 | 4.67 | -0.17 |
| 0,17 | 4.24 | 4.41 | -0.18 |
| 0,18 | 4.00 | 4.19 | -0.19 |
| 0,19 | 3.79 | 3.98 | -0.20 |
| 0.20 | 3.60 | 3.80 | -0.20 |
Почему именно 72? Необязательно точное значение 72. Это просто число, которое хорошо подходит для реалистичных процентных ставок, которые вы, вероятно, увидите при инвестировании. Оно почти точно соответствует процентной ставке 7,8469%. В числе 72 нет ничего особенного, как, например, в π или e. Почему любое число подходит? Если процентная ставка равна i, то давайте вычислим количество лет (y), необходимых для удвоения инвестиций.
2 = (1+i) y
ln(2) = ln(1+i) y
ln(2) = y × ln(1 + i)
y = ln(2)/ln(1+i)
Возможно, это не самый лучший мой ответ, но попробуйте следовать этой логике: пусть y = ln(x).
dy/dx=1/x.
1/x ≈ x при значениях x, близких к 1.
Таким образом, dy/dx ≈ 1 для значений x, близких к 1.
Таким образом, наклон графика ln(x) будет близок к 1 при значениях x, близких к 1.
Таким образом, наклон графика ln(1+x) будет близок к 1 при значениях x, близких к 0.
«Правило 72» гласит, что 0,72/i ≈ 0,6931/ln(1+i).
Мы установили, что i и ln(1+i) подобны для значений i, близких к 0.
Таким образом, 1/i и 1/ln(1+i) похожи для значений i, близких к 0.
Использование 72 вместо 69,31 позволяет скорректировать различия между i и ln(1+i) для значений i около 8%.
Надеюсь, это хоть как-то понятно. Мои знания математического анализа довольно сильно подзабылись; мне потребовались часы, чтобы разобраться в этом самостоятельно.
Этот вопрос был поднят и обсужден на форуме моего дочернего сайта Wizard of Vegas .
На недавней уличной ярмарке была игра, в которой на поле были числа, неглубокие стаканчики и стаканчик с шариками, и она включала в себя сложение. Я не спрашивал название игры и около часа искал информацию в интернете, но ничего не нашел. Я подумал, что у вас может быть какая-то информация о ней, о вероятности успеха или хотя бы о названии.
В индустрии эту игру называют «Разгром». Я помню, как в детстве видел её в Южной Калифорнии, а совсем недавно, в прошлом году, в Сан-Фелипе, Мексика. Обычно её оформляют так, чтобы она выглядела как футбольный матч. На мой взгляд, это худшая из всех афер на карнавалах. Штату Нью-Йорк должно быть стыдно за то, что он её разрешает. Судя по некоторым исследованиям, правила различаются в зависимости от места, но суть аферы всегда одна и та же.
В основе этой ставки лежит та же иллюзия, что и в крэпсе. Для тех читателей, кто не знаком с этой ставкой, поясним: игрок выигрывает, если сумма выпавших на двух кубиках чисел равна 2, 3, 4, 9, 10, 11 или 12. Проигрышные числа — 5, 6, 7 и 8. Выигрышные числа выплачиваются в равных суммах, за исключением 2, где выплата составляет 2 к 1, а 12 — 3 к 1 (кроме скупых казино Harrah's, где выплата 2 к 1 производится только на 12). Игрок, не разбирающийся в математике, может ошибочно предположить, что это хорошая ставка, потому что существует 7 выигрышных сумм и только 4 проигрышных. Причина, по которой шансы на стороне казино, заключается в том, что проигрышные числа имеют наибольшую вероятность выпадения.
Вот конкретные правила игры Razzle Dazzle, взятые из статьи Дональда А. Берри и Рональда Р. Регала «Вероятности выигрыша в определенной карнавальной игре» , опубликованной в ноябрьском номере журнала The American Statistician за 1978 год.
- Цель игры — продвинуться по футбольному полю на 100 ярдов. За это игрок получит какой-нибудь приятный приз.
- Игрок начинает платить определенную сумму за каждую игру, например, 1 доллар.
- Игрок должен высыпать 8 шариков на сетку размером 11 на 13. Каждый шарик упадет в одно из 143 отверстий.
- В каждом отверстии находится количество точек от 1 до 6. В следующей таблице показана частота встречаемости каждого количества точек.
Распределение баллов Razzle Dazzle
Баллы Число
на бортуВероятность 1 11 0.076923 2 19 0.132867 3 39 0.272727 4 44 0.307692 5 19 0.132867 6 11 0.076923 Общий 143 1.000000 - Общее количество очков будет суммировано. Работник аттракциона посмотрит сумму очков в таблице пересчета, чтобы узнать, на сколько ярдов продвинулся игрок. Таблица пересчета показана ниже.
Таблица конверсий Razzle Dazzle
Баллы Дворы
Получено8 100 9 100 10 50 11 30 12 50 13 50 14 20 15 15 16 10 17 5 от 18 до 38 0 39 5 40 5 41 15 42 20 43 50 44 50 45 30 46 50 47 100 48 100 - Если игрок выбросит в сумме 29, то плата за все последующие броски будет удвоена, и игрок получит один дополнительный приз, если и когда он достигнет другого конца футбольного поля.
Среднее количество очков на один шарик составляет 3,52, а стандартное отклонение — 1,31. Обратите внимание, что 3 и 4 очка имеют наибольшую вероятность. Это позволяет поддерживать низкое стандартное отклонение, и сумма результатов броска многих шариков близка к ожидаемой. Для сравнения, стандартное отклонение броска одной игральной кости составляет 1,71.
Далее, обратите внимание, что в таблице пересчета ярдов указано 20 выигрышных и 21 проигрышный вариант. Тот, кто играет в азартные игры на ярмарках, может ошибочно предположить, что вероятность его выхода в следующий раунд составляет 20/41 или 48,8%. Меня бы не удивило, если бы работники ярмарки ложно утверждали, что это шансы на выход в следующий раунд. Однако, как и в случае со ставкой на поле, наиболее вероятные исходы ничего не выигрывают.
В следующей таблице показана вероятность каждого количества очков за ход, количество набранных ярдов и ожидаемое количество набранных ярдов. В нижней правой ячейке указано среднее количество набранных ярдов за ход, равное 0,0196.
Ожидаемое количество ярдов, набранных за ход
| Баллы | Вероятность | Дворы Получено | Ожидал Дворы Получено |
| 8 | 0.00000000005 | 100 | 0.00000000464 |
| 9 | 0.00000000176 | 100 | 0.00000017647 |
| 10 | 0.00000002586 | 50 | 0.00000129285 |
| 11 | 0.00000022643 | 30 | 0.00000679305 |
| 12 | 0.00000143397 | 50 | 0.00007169849 |
| 13 | 0.00000713000 | 50 | 0.00035650022 |
| 14 | 0.00002926510 | 20 | 0.00058530196 |
| 15 | 0.00010234709 | 15 | 0.00153520642 |
| 16 | 0.00031168305 | 10 | 0.00311683054 |
| 17 | 0.00083981462 | 5 | 0.00419907311 |
| 18 | 0.00202563214 | 0 | 0.00000000000 |
| 19 | 0.00441368617 | 0 | 0.00000000000 |
| 20 | 0.00874847408 | 0 | 0.00000000000 |
| 21 | 0.01586193216 | 0 | 0.00000000000 |
| 22 | 0.02642117465 | 0 | 0.00000000000 |
| 23 | 0.04056887936 | 0 | 0.00000000000 |
| 24 | 0.05757346716 | 0 | 0.00000000000 |
| 25 | 0.07566411880 | 0 | 0.00000000000 |
| 26 | 0.09221675088 | 0 | 0.00000000000 |
| 27 | 0.10431970222 | 0 | 0.00000000000 |
| 28 | 0.10958441738 | 0 | 0.00000000000 |
| 29 | 0.10689316272 | 0 | 0.00000000000 |
| 30 | 0.09677806051 | 0 | 0.00000000000 |
| 31 | 0.08125426057 | 0 | 0.00000000000 |
| 32 | 0.06317871335 | 0 | 0.00000000000 |
| 33 | 0.04540984887 | 0 | 0.00000000000 |
| 34 | 0.03009743061 | 0 | 0.00000000000 |
| 35 | 0.01833921711 | 0 | 0.00000000000 |
| 36 | 0.01023355162 | 0 | 0.00000000000 |
| 37 | 0.00520465303 | 0 | 0.00000000000 |
| 38 | 0.00239815734 | 0 | 0.00000000000 |
| 39 | 0.00099365741 | 5 | 0.00496828705 |
| 40 | 0.00036673565 | 5 | 0.00183367827 |
| 41 | 0.00011909673 | 15 | 0.00178645089 |
| 42 | 0.00003349036 | 20 | 0.00066980729 |
| 43 | 0.00000797528 | 50 | 0.00039876403 |
| 44 | 0.00000155945 | 50 | 0.00007797235 |
| 45 | 0.00000023832 | 30 | 0.00000714969 |
| 46 | 0.00000002632 | 50 | 0.00000131607 |
| 47 | 0.00000000176 | 100 | 0.00000017647 |
| 48 | 0.00000000005 | 100 | 0.00000000464 |
| Итоговые суммы | 1.00000000000 | 0 | 0.01961648451 |
Вот некоторые результаты случайного моделирования 17,5 миллионов игр.
Результаты моделирования Razzle Dazzle
| Вопрос | Отвечать |
| Вероятность продвижения за ход | 0,0028 |
| Ожидаемое количество ярдов, набранных за ход | 0,0196 |
| Ожидаемое количество ярдов, набранных за каждое продвижение. | 6.9698 |
| Ожидаемое количество ходов за игру | 5238.7950 |
| Среднее количество парных матчей за игру | 559.9874 |
| Средние призы за игру | 560.9874 |
Мне бы хотелось указать среднюю общую ставку за игру, но мой компьютер не может обрабатывать такие большие числа. В среднем игрок удваивал свою ставку 560 раз за 5239 ходов в игре. В одной из игр в симуляции игрок удваивал свою ставку 1800 раз. Даже при среднем количестве удвоений в 560, ставка за один бросок составила бы 3,77 × 10¹⁶⁸ долларов, при условии начальной ставки в 1 доллар. Это на много порядков больше, чем количество атомов в известной Вселенной ( источник ).
Даже самый наивный игрок не будет долго играть, если он продвигается вперед только раз в 355 ходов. Поначалу торговцы будут жульничать в пользу игрока. Они могут подсовывать игроку бесплатные броски или лгать при подсчете очков, давая игроку выигрышные суммы, чтобы поднять его уверенность. Я никогда не играл в эту игру, но предполагаю, что когда игрок приблизится к красной зоне (20 ярдов или меньше до тачдауна), торговец начнет играть честно. Игрок может удивляться, почему он вдруг никуда не продвигается, но, уже вложив деньги и находясь так близко к линии ворот, он будет колебаться, прежде чем уйти и отдать уже заплаченные ярды.
Ссылки
- «Блеск и ослепительность» — отрывок из книги «На Мидуэе».
- Афера с настольной игрой Razzle Dazzle Carny Board Game Arcade .
- Вероятности выигрыша в определенной карнавальной игре (авторы: Дональд А. Берри и Рональд Р. Регал)
На недавнем карнавале предлагалась игра в стиле крестиков-ноликов. За 1 фунт стерлингов нужно было бросить три невероятно прыгучих мячика в большой деревянный ящик с 9 лунками внизу. Предположим, что каждый мячик попадает в уникальное поле. Какова вероятность выигрыша?
Существует восемь способов выиграть: три ряда, три столбца и две диагонали. Комбинаций (9,3) = 84, чтобы выбрать 3 клетки из 9. Таким образом, вероятность выигрыша составляет 8/84 = 9,52%.
Этот вопрос был поднят и обсужден на форуме моего дочернего сайта Wizard of Vegas .
Какой совет вы можете дать по игре в «Монополию»?
Вот базовая стратегия моего Волшебника в игре «Монополия»:
- Скупайте всё. Опытные игроки могут сделать исключения, если недвижимость не поможет вам создать монополию, не заблокирует действия другого игрока и не представляет большой ценности в качестве козыря в переговорах. В случае нехватки денежных средств от коммунальных услуг также можно отказаться.
- Торгуйте как можно эффективнее. Здесь вступает в игру мастерство. Старайтесь обменять их на лучший набор карт, какой только сможете. Вот как я их ранжирую в целом: оранжевый, жёлтый, светло-голубой, тёмно-синий, светло-фиолетовый, красный, зелёный, тёмно-фиолетовый. Это может меняться в зависимости от обстоятельств. В игре с ограниченными средствами отдавайте предпочтение наборам, которые дешевле развивать, например, светло-голубым. В игре с большими средствами выбирайте те, на которые есть больше возможностей потратить деньги, например, жёлтые или тёмно-синие.
- Как только вы обзаведетесь домом, естественным путем или в результате обмена, наращивайте его как можно быстрее. Постарайтесь как можно быстрее построить по три дома на каждом участке. После трех домов предельная доходность с каждого построенного дома падает. Заложите большую часть оставшейся недвижимости и тратьте свои деньги. Вам нужно оставить немного средств на мелкие расходы. Не тратить деньги — это как солдат в бою, не использующий свои патроны.
- Выступайте против всех нелепых правил игры. Особенно это касается денежного приза в игре «Бесплатная парковка» (я терпеть её не могу!). Если вы более опытны, чем ваши противники, вы должны свести к минимуму случайность в игре.
Если обезьяна играет с кубиком Рубика, какова вероятность того, что в любой момент времени он окажется в собранном виде?
Шесть центральных граней куба неподвижны. Поворачивая грани, можно лишь переставлять углы и ребра. Если разобрать куб, то получится 8! = 40 320 способов расположить восемь углов, не принимая во внимание ориентацию каждой детали. Аналогично, существует 12! = 479 001 600 способов расположить 12 ребер, не принимая во внимание ориентацию.
Каждый угол может быть ориентирован тремя способами, что в сумме составляет 3 8 = 6561 вариантов ориентации угла. Аналогично, каждый краевой элемент может быть ориентирован двумя способами, что в сумме составляет 2 12 = 4096 вариантов ориентации края.
Итак, если бы мы могли разобрать куб и переставить группы ребер и углов, то получили бы 8! × 12! × 3 8 × 2 12 = 519 024 039 293 878 000 000 возможных перестановок. Однако не все из этих перестановок можно получить из исходного положения, вращая грани.
Во-первых, невозможно повернуть только один угол, оставив все остальное без изменений. Никакая комбинация поворотов этого не обеспечит. По сути, каждое действие должно вызывать противодействие. Если вы захотите повернуть один угол, это каким-то образом повлияет на другие фигуры. Точно так же невозможно перевернуть только одну реберную фигуру. По этим причинам нам приходится делить количество перестановок на 3 × 2 = 6.
Во-вторых, невозможно поменять местами две ребра, не нарушив целостность кубика. Это самая сложная часть ответа для объяснения. Все, что можно сделать с кубиком Рубика, — это вращать по одной грани за раз. Каждое движение поворачивает четыре ребра и четыре угловых элемента, всего перемещается восемь элементов. Последовательность вращений может быть представлена числом перемещений элементов, делящимся на 8. Часто последовательность движений приводит к тому, что два движения взаимно компенсируются. Однако при любой последовательности вращений всегда будет перемещено четное число элементов. Поменять местами два ребра — это одно движение, нечетное число, чего нельзя достичь суммой любых четных чисел. Математики назвали бы это проблемой четности. Поэтому нам нужно разделить на 2, потому что два ребра нельзя поменять местами, не нарушив целостность других элементов.
Таким образом, существует 3 × 2 × 2 = 12 возможных групп перестановок кубика Рубика. Если разобрать кубик Рубика и собрать его случайным образом, то вероятность того, что он будет решён, составляет 1 к 12. Следовательно, общее количество перестановок в кубике Рубика равно 8! × 12! × 3 12 × 2 12 / 12 = 43 252 003 274 489 900 000. Если бы у вас было семь миллиардов обезьян, примерно равных численности населения Земли, которые случайным образом играли бы с кубиком Рубика со скоростью один оборот в секунду, то в среднем один кубик проходил бы через решённое положение раз в 196 лет.
Ссылки
Я играл в «Червы» и мне выпало 10 червей. Какова вероятность этого?
Для тех, кто не знаком с правилами игры в «Червы», игра начинается с раздачи по 13 карт каждому из четырех игроков. Масть червей имеет значение в игре, поэтому количество полученных карт важно. В следующей таблице показаны шансы получить от 0 до 13 червей.
Вероятность выпадения от 0 до 13 червей из 13 карт.
| Сердца | Комбинации | Вероятность | Обратная |
|---|---|---|---|
| 13 | 1 | 0.0000000000016 | 1 из 635 013 559 600,0 |
| 12 | 507 | 0.0000000007984 | 1 из 1 252 492 228,0 |
| 11 | 57,798 | 0.0000000910185 | 1 из 10 986 773,9 |
| 10 | 2 613 754 | 0.0000041160601 | 1 из 242 950,8 |
| 9 | 58,809,465 | 0.0000926113531 | 1 из 10 797,8 |
| 8 | 740,999,259 | 0.0011669030492 | 1 из 857,0 |
| 7 | 5 598 661 068 | 0.0088166008164 | 1 из 113,4 |
| 6 | 26,393,687,892 | 0.0415639752774 | 1 из 24,1 |
| 5 | 79,181,063,676 | 0.1246919258321 | 1 из 8,0 |
| 4 | 151,519,319,380 | 0.2386080062219 | 1 из 4,2 |
| 3 | 181,823,183,256 | 0.2863296074662 | 1 из 3,5 |
| 2 | 130,732,371,432 | 0.2058733541286 | 1 из 4,9 |
| 1 | 50,840,366,668 | 0.0800618599389 | 1 из 12,5 |
| 0 | 8,122,425,444 | 0.0127909480376 | 1 из 78,2 |
| Общий | 635,013,559,600 | 1.0000000000000 |
Этот вопрос был поднят и обсужден на форуме моего дочернего сайта Wizard of Vegas .
В казино, где до сих пор используются обычные билеты в настоящем барабане (не электронные), которые вы распечатываете на стойке игрока и опускаете в барабан, — вы сгибаете/мнёте билеты перед тем, как положить их в барабан? Считаете ли вы, что согнутые билеты имеют больше шансов быть выбранными?
Надеюсь, вы довольны. Чтобы ответить на этот вопрос, я купил большой рулон билетов в магазине Office Depot. Затем я положил 500 билетов в бумажный пакет, половину сложив пополам примерно под углом 90 градусов, а другую половину развернув. Затем шесть добровольцев по очереди вытаскивали от 40 до 60 билетов, возвращая их обратно, а я записывал результаты. Вот результаты.
Эксперимент с розыгрышем билетов
| Предмет | Сложенный | Развернуто | Общий |
|---|---|---|---|
| 1 | 25 | 25 | 50 |
| 2 | 38 | 22 | 60 |
| 3 | 25 | 15 | 40 |
| 4 | 34 | 16 | 50 |
| 5 | 27 | 23 | 50 |
| 6 | 26 | 24 | 50 |
| Общий | 175 | 125 | 300 |
Таким образом, 58,3% выпавших билетов были сложены!
Если предположить, что складывание не оказало никакого влияния, то эти результаты будут отличаться от ожиданий на 2,89 стандартных отклонения. Вероятность получить такое количество сложенных билетов или больше, если предположить, что складывание не повлияло на шансы, составляет 0,19%, или 1 к 514.
Добавлю, что те, кто быстро вытаскивал билеты, гораздо чаще вытаскивали сложенные. У тех, кто тщательно выбирал билеты, соотношение было примерно 50/50.
Итак, мой вывод однозначно таков: их нужно сложить.
Для обсуждения этого вопроса, пожалуйста, посетите мой форум на сайте Wizard of Vegas .