Вероятность - Монеты
Если монету подбросить 1000 раз, какова вероятность того, что общее количество выпавших орлов окажется в диапазоне от 452 до 548?
Для решения этой задачи мы можем использовать нормальную аппроксимацию биномиального распределения. Дисперсия числа выпавших орлов равна 1000*(1/2)*(1/2)=250. Следовательно, стандартное отклонение равно 250 1/2 = 15,8114. Вероятность выпадения менее 548 орлов равна normdist((548+0,5-500)/15,8114) = 0,998920, где normdist — это функция Excel для вероятности того, что случайная величина со средним значением 0 и стандартным отклонением 1 окажется ниже заданного Z-балла. Далее вычитаем вероятность выпадения менее 452 орлов. Это normdist((452-0,5-500)/15,8114) = 0,001080. Таким образом, ответ равен 0,99892-0,00108 = 0,997840. Опять же, это аппроксимация. Фактический ответ — 0,997856, но его вычисление более трудоемко. В среднем, после установления точки в игре в кости, как часто игрок будет её устанавливать?
Учитывая, что точка была установлена, в 5/12 случаев это будет 6 или 8, в 4/12 — 5 или 9, и в 3/12 — 4 или 10. Вероятность получить 6 или 8 составляет 5/11, 5 или 9 — 4/10, а 4 или 10 — 3/9. Таким образом, вероятность установить точку, при условии, что она была установлена, составляет (5/12)*(5/11)+(4/12)*(4/10)+(3/12)*(3/9) = 40,61%.
Уважаемый господин Волшебник, если 50 разных человек подбрасывают монету в воздух 8 раз, какой процент из этих 50 человек выбросит 8 раз подряд орла или решку? Заранее благодарю.
Вероятность того, что любой человек выбросит 8 орлов или решек, составляет 2*(1/2) 8 = 1 к 128. Если 50 человек сделают это в среднем, то 0,39 из них получат все орлы или решки. Вероятность того, что хотя бы один человек получит все орлы или решки, составляет 32,44%.
У меня есть мешок со 100 монетами, одна из них — двусторонняя. Я наугад выбираю монету и наблюдаю, как она выпадает 10 раз подряд орлом. Какова вероятность того, что я выбрал двустороннюю монету?
Это классический пример задачи на байесовскую условную вероятность. В общем случае вероятность события А при условии события В равна вероятности событий А и В, деленной на вероятность события В. В данном случае А подбрасывает 10 орлов подряд, а В выбирает монету с двумя орлами. Вероятность событий А и В равна 1/100. Это потому, что вероятность выбрать монету с двумя орлами составляет 1 к 100, а если это произойдет, то вероятность выпадения 10 орлов подряд составляет 100%. Вероятность выпадения 10 орлов подряд, при условии случайного выбора монеты, равна (1/100)*1 + (99/100)*(1/2) 10. Это потому, что вероятность выбрать монету с двумя орлами составляет 1%, что соответствует 100% вероятности выпадения 10 орлов, а вероятность выбрать честную монету, которая соответствует (1/2) 10 вероятности выпадения 10 орлов подряд, составляет 99%. Таким образом, вероятность того, что вы выбрали монету с двумя орлами, при условии, что вы подбросили 10 орлов подряд, составляет 0,01/(0,01*1 + 0,99* 0,000977) = 0,911843.
У вас есть какие-нибудь советы по ставкам на подбрасывание монеты?
Да! Мой совет: в начале подбрасывания делайте ставку на верхнюю сторону монеты. Согласно Science News Online, вероятность того, что монета упадет на ту же сторону, с которой она начала, составляет 51%. В статье говорится, что причина в том, что подброшенная монета не вращается идеально вокруг своей оси и иногда кажется, что она подбрасывается, хотя на самом деле это не так. Эта гипотеза применима только в том случае, если монета находится в ладони, поэтому отскок не является проблемой. В статье также говорится, что вращающаяся монета в 80% случаев выпадет решкой, поскольку более тяжелая сторона с орлом стремится упасть первой. Однако я скептически отношусь к этому. Я попробовал это 20 раз и получил 11 орлов и 9 решек. Вероятность получить 9 или меньше решек за 20 вращений с вероятностью успеха 80% составляет 1 к 1775.
Я думаю, у меня есть ответ на вопрос о вращающейся монетке. Более десяти лет назад, в шестом классе, я делал научный проект о вращении монетки. В журнале Omni я прочитал, что при очень быстром вращении монетка почти всегда останавливается решкой вверх, потому что боковые стороны наклоняются к орлу. Я пробовал это сотни раз и получал почти объективные результаты, за исключением двух случаев, когда монетка стояла ребро.
После множества потраченных впустую часов я наконец обнаружил, что вращал монетку слишком быстро, и более медленное вращение дало желаемый результат, то есть решку вверх. Кроме того, монетка не совсем ровная, и начало вращения с самой тонкой части, кажется, улучшило её равномерность. Несколько таблиц, полных всякой ерунды, и огромный картонный круг, украшенный как монетка, принесли мне пятёрку по естествознанию и провалы по всем остальным предметам, поскольку я игнорировал все домашние задания.
Таким образом, с помощью одного грубо проведенного эксперимента, выполненного более десяти лет назад (я почти ничего о нем не помню и тогда понятия не имел, что делаю), я убедительно доказал, что вы, возможно, просто слишком быстро раскручиваете свою монетку.
Хорошо, я попробовал еще раз, медленно вращая монетку 100 раз. Под «медленно» я подразумеваю время между броском и моментом, когда результат становился очевидным, не менее двух секунд, но менее пяти. Я использовал красивую блестящую монетку 2004-D. В результате получилось 52 орла и 48 решек. Так что я по-прежнему не убежден, что вращающаяся монетка на любой скорости сильно склоняется к выпадению решек.
В моем понимании «время ожидания» события — это величина, обратная вероятности этого события. Меня интересует расчет времени ожидания до выпадения двух подряд выпавших чисел на одной игральной кости. В симуляции я получаю в среднем 42 броска. Как мне установить связь с вероятностью выпадения двух подряд выпавших чисел?
Действительно, для одиночных событий, если вероятность равна p, то среднее время ожидания составляет 1/p. Однако с последовательными событиями ситуация усложняется. Пусть x — состояние, в котором последний бросок не выпал на двойку. Это также состояние в начале. Пусть y — состояние, в котором последний бросок выпал на двойку. После первого броска вероятность того, что мы останемся в состоянии x, составляет 5/6, а вероятность того, что мы останемся в состоянии y, — 1/6. Пусть Ex(x) — ожидаемое количество бросков из состояния x, а Ex(y) — ожидаемое количество из состояния y. Тогда...
Ex(x) = 1 + (5/6)*ex(x) + (1/6)*ex(y), и
Ex(y) = 1 + (5/6)*ex(x)
Решая эти два уравнения...
Ex(x) = 1 + (5/6)*ex(x) + (1/6)*( 1 + (5/6)*Ex(x))
Ex(x) = 7/6 + (35/36)*Ex(x)
(1/36)*Ex(x) = 7/6
Ex(x) = 36*(7/6) = 42
Таким образом, среднее время ожидания двух последовательных двоек составляет 42 броска кубика.
У меня похожая проблема, только для получения двух орлов нужны ожидаемые подбрасывания кубика. На моем сайте с математическими задачами , смотрите задачу 128.
Предположим, у нас есть азартная игра. Монета без форы подбрасывается несколько раз. За каждый бросок мы должны заплатить 1 рупию. Возможны два исхода: H или T. Если разница между выпадением орла и решки равна 3, мы получим от игрока 8 рупий. Стоит ли нам играть в эту игру и почему? Какова наша вероятность выигрыша? Как повлияет на вероятность выигрыша получение 7 или 9 рупий?
Назовем x ожидаемым числом бросков относительно начальной точки.
Назовем y ожидаемым числом оставшихся бросков, если одна из сторон выигрывает один раз из большинства.
Назовем z ожидаемым числом оставшихся бросков, если одна сторона имеет преимущество в два броска в большинстве.
E(x) = 1 + E(y)
E(y) = 1 + 0,5*E(x) + 0,5*E(z)
E(z) = 1 + 0,5*E(y)
Затем, с помощью матричных алгебраических вычислений, легко увидеть, что E(x) = 9, E(y) = 8 и E(z) = 5. Таким образом, в среднем потребуется 9 бросков, чтобы разница между орлом и решкой составила 3. Поэтому ставка в 8 рупий является выгодной для игрока, получающего одну рупию за бросок, поскольку в среднем он получит 9 рупий, но вернет только 8. Преимущество казино для игрока составляет 11,11%. При ставке в 9 рупий это справедливая ставка, при 7 рупиях преимущество казино составляет 22,22%.
В своей рубрике «Спроси волшебника» от 13 марта 2006 года вы привели три формулы для игры в «рупии». Хотя решение математически верно, я никак не могу понять, как эти три уравнения моделируют задачу. Не могли бы вы объяснить, как вы пришли к этим трем уравнениям?
Несколько человек попросили меня подробнее объяснить свой ответ. Для решения требуется базовая матричная алгебра.
Начните с того, что обозначьте x как ответ, или среднее количество бросков, при котором разница между орлом и решкой становится равной 3.
Пусть y — ожидаемое количество бросков из точки, где одна сторона находится выше на один бросок.
Пусть z — ожидаемое количество бросков из точки, где одна сторона находится выше на два броска.
После первого броска одна из сторон окажется в большинстве на один бросок. Следовательно, x = 1 + y.
Когда одна из сторон опережает другую на один ход, следующий ход приведет либо к первоначальному ничейному состоянию, либо к тому, что одна из сторон окажется впереди на два хода. Оба исхода одинаково вероятны. Таким образом, y = 1 + 0,5*x + 0,5*z
Когда одна из сторон опережает другую на два броска, следующий бросок приведет либо к тому, что одна из сторон окажется впереди на один бросок, либо к концу игры. Опять же, оба исхода одинаково вероятны. Таким образом, z = 1 + 0,5 * y
Таким образом, у нас есть три уравнения и три неизвестных:
(1) X = 1 + y
(2) Y = 1 + 0,5x + 0,5z
(3) Z = 1 + 0,5y
Для решения давайте сначала избавимся от десятичных знаков, умножив последние два уравнения на 2.
(1) X = 1 + y
(2) 2Y = 2 + x + z
(3) 2Z = 2+ y
Подставим 1+y из (1) вместо x в (2).
2Y = 2 + 1 + y + z
(4) y = 3 + z
В (3) нет замены 3+z на y.
2z = 2 + 3 + z
z = 5
Теперь подставим 5 вместо z в (4), чтобы получить
(5) y = 3 + 5 = 8
Подстановка y = 8 в (1) не дает
(6) x = 9
Друг выбирает последовательность из трех бросков монеты: орел или решка, и предлагает мне выбрать свою собственную (другую) последовательность из трех бросков. Мы подбрасываем честную монету столько раз, сколько необходимо, пока не выпадет одна из наших последовательностей. Если он выберет HHH, какую последовательность должен выбрать я, и в чем мое преимущество в этой ставке? Как мне рассчитать, какую последовательность выбрать, исходя из выбранной им последовательности?
В следующей таблице показана вероятность выигрыша игрока А при всех возможных вариантах развития событий, выбранных игроком А и игроком В.
Вероятность победы игрока А
| Игрок А | Игрок Б | |||||||
| ХХХ | ХХТ | СПАСИБО | ХТТ | ТХХ | ТХТ | ТТХ | ТТТ | |
| ХХХ | 1/2 | 2/5 | 2/5 | 1/8 | 5/12 | 3/10 | 1/2 | |
| ХХТ | 1/2 | 2/3 | 2/3 | 1/4 | 5/8 | 1/2 | 7/10 | |
| СПАСИБО | 3/5 | 1/3 | 1/2 | 1/2 | 1/2 | 3/8 | 7/12 | |
| ХТТ | 3/5 | 1/3 | 1/2 | 1/2 | 1/2 | 3/4 | 7/8 | |
| ТХХ | 7/8 | 3/4 | 1/2 | 1/2 | 1/2 | 1/3 | 3/5 | |
| ТХТ | 7/12 | 3/8 | 1/2 | 1/2 | 1/2 | 1/3 | 3/5 | |
| ТТХ | 7/10 | 1/2 | 5/8 | 1/4 | 2/3 | 2/3 | 1/2 | |
| ТТТ | 1/2 | 3/10 | 5/12 | 1/8 | 2/5 | 2/5 | 1/2 | |
Для выбора оптимальной комбинации карт, учитывающей особенности вашей стратегии, первым и вторым выбором оппонента должны быть ваши второй и третий выборы соответственно. Ваш первый выбор должен быть противоположным третьему. Например, если ваш оппонент выбирает HTT, ваши второй и третий выборы должны быть HT. Ваш последний выбор — T, поэтому ваш первый выбор должен быть H, если комбинация HHT. Следуя этой стратегии, ваша вероятность выигрыша составит от 2/3 до 7/8, в зависимости от того, какую комбинацию выберет оппонент.
Здравствуйте, меня зовут Пэтти. У вас очень хороший сайт, и вы, кажется, очень знающий человек. Определенно, именно такого мужчину я хочу видеть рядом с собой в казино!!! Я хотела бы узнать, можете ли вы мне помочь. Я сказала своему парню, что поищу ответ на свой вопрос в интернете. Если вы мне поможете, это действительно выставит меня в лучшем свете.
Мой парень — коллекционер монет. Он купил мешок пенни с изображением пшеничного колоса. Я сама мало что знаю о монетах (он меня учит со временем). Но он сказал, что был поражен тем, что в мешке не оказалось монет одного определенного года выпуска, ведь они такие распространенные. Он сказал, что вероятность такого совпадения — миллиард к одному. Я сказала ему, что попробую спросить у коллег в офисе (самопровозглашенных гениев!!), и если они не знают, я попробую поискать информацию в интернете. И тут я наткнулась на вас.
В любом случае, если вы можете помочь, я буду очень признателен. В мешке было примерно 5500 пенни. Общее количество пенни с изображением пшеничного колоса, отчеканенных всеми монетными дворами США, составляло 24 267 000 000. Количество отчеканенных в 1955 году пенни (тот, который он искал) составляло 330 000 000. Некоторые ребята в моем офисе говорят, что есть и другие факторы, такие как демографические данные, тот факт, что монетные дворы могли не распределить все пенни и т. д. ................................... Я предполагаю, что они правы, но я (и я уверен, что мой парень тоже) был бы рад узнать приблизительные шансы!!!!!!!!! Надеюсь, вы сможете помочь.
Ваши тиражи близки к тиражам Mountain View Coins . Предполагая, что каждая когда-либо отчеканенная монета достоинством в один пенни с изображением пшеничного колоса имеет одинаковую вероятность оказаться в мешке, вероятность того, что любая монета не будет иметь номер 55, составляет (24 267 000 000 - 330 000 000) / 24 267 000 000 = 0,986401286. Вероятность того, что 5500 монет не будут иметь номер 55, можно очень точно оценить как 0,986401286. 5500 = 1 из 507 033 772 284 213 000 000 000 000 000 000.
Мой отец — коллекционер монет, поэтому я попросил его помочь мне в этом вопросе. Вот что он сказал:
Вот моя догадка. В 1955 году в Филадельфии было отчеканено небольшое количество центов с изображением Линкольна, на которых дата была указана дважды. Никто точно не знает, сколько именно. Они были смешаны с другими центами для обращения до того, как ошибка была обнаружена. Сегодня экземпляр в идеальном состоянии стоит от 2000 до 6000 долларов. Я подозреваю, что из мешка с «пшеничными» монетами уже были отобраны все монеты 1955 года кем-то, кто искал экземпляры с двойным штампом. Вот фотография одной из таких монет: 1955 год, аверс, двойной штамп, один цент .
Обратите внимание, что на этом сайте продаются «пшеничные пенни», и можно с уверенностью сказать, что после того, как монеты были собраны дилером, произошла некоторая сортировка по датам. Я бы предположил, что пенни 1955 года, не имеющие двойного штампа, были бы возвращены в коллекцию, но, возможно, они продаются отдельно или переплавляются. Медь в пшеничных пенни сегодня стоит гораздо больше одного цента. Именно поэтому несколько десятилетий назад перешли на медные цинковые центы. Возможно, сам монетный двор решил не распространять многие пенни 1955 года и переплавил их после чеканки, чтобы избежать ажиотажа вокруг редких экземпляров с двойным штампом. Монетный двор и Почта всегда стеснялись ошибок печати и стараются не допускать их попадания в обращение.
В своей последней колонке вы написали: «Вероятность того, что 5500 монет не будут иметь число 55, можно очень точно оценить как 0,9864012865500 = 1 к 507 033 772 284 213 000 000 000 000 000 000».
Я предполагаю, что это «приблизительно», потому что эффект удаления монет происходит по мере того, как вы проходите через 5500 монет. Это же ничтожно малый эффект удаления! Это хороший пример того, как вероятность выпадения целевых монет уменьшается по мере удаления нецелевых, потому что эффект удаления настолько мал по сравнению с гораздо большей вероятностью нечестной игры, то есть когда целевые монеты удалены.
Да, я сказал «приблизительно», потому что в мире не так уж много пенни. Удалите из мешка один пенни, не равный 55, и эффект удаления увеличит вероятность того, что каждый второй пенни в мешке будет иметь число 55. Если бы я не сказал «приблизительно», по крайней мере три человека написали бы мне, чтобы меня поправить. Конечно, это крайне незначительный эффект, но многие из моих читателей — перфекционисты, и они набросятся на меня из-за малейшей ошибки.
В комнате два стола. На столе справа лежат 100 монет: 20 с буквой «H» вверху и остальные (80) с буквой «T» вверху. На другом столе монет нет. Задача состоит в том, чтобы каким-то образом переместить монеты так, чтобы на обоих столах оказалось одинаковое количество монет с буквой «H» вверху. Монеты нельзя увидеть (комната темная) или потрогать, чтобы определить, повернуты они «вверх» или «вниз».
Решение можно найти на моём другом сайте, mathproblems.info (осторожно, спойлер!).
Мой друг предложил мне пари на 20 долларов, предложив коэффициент 3 к 1, что если я подброшу монету 100 раз, то выпадет ровно 50 орлов и 50 решек. В этом случае я выиграю 60 долларов, а в противном случае буду должен ему 20 долларов. Стоило ли мне принять это пари? Кроме того, если 50/50 — не самый вероятный исход, есть ли другой исход (например, 51/49), который более вероятен?
Вероятность получить ровно 50 каждого вида равна (100,50)*(1/2) 100 = 7,96%. Справедливые шансы составили бы 11,56 к 1. Таким образом, при коэффициенте 3 к 1 это ужасная ставка с преимуществом казино в 68,2%. Вот уж у вас друг. 50/50 — наиболее вероятное точное разделение между орлом и решкой. Интересная ставка — попадет ли количество орлов/решек в диапазон от 47 до 53 или нет. Вероятность попадания в этот диапазон составляет 51,59%. Если вы найдете кого-нибудь, кто поставит на то, что сумма выйдет за пределы этого диапазона, то при равных шансах у вас будет преимущество в 3,18%.
В следующей таблице показана вероятность выпадения каждого из 30-70 орлов/решек.
Вероятность выпадения орла/решки за 100 бросков кубиков.
| Орёл/Решка | Вероятность |
|---|---|
| 30, 70 | 0.000023 |
| 31, 69 | 0.000052 |
| 32, 68 | 0.000113 |
| 33, 67 | 0.000232 |
| 34, 66 | 0.000458 |
| 35, 65 | 0.000864 |
| 36, 64 | 0.001560 |
| 37, 63 | 0.002698 |
| 38, 62 | 0.004473 |
| 39, 61 | 0.007111 |
| 40, 60 | 0.010844 |
| 41, 59 | 0.015869 |
| 42, 58 | 0.022292 |
| 43, 57 | 0.030069 |
| 44, 56 | 0.038953 |
| 45, 55 | 0.048474 |
| 46, 54 | 0.057958 |
| 47, 53 | 0.066590 |
| 48, 52 | 0.073527 |
| 49, 51 | 0.078029 |
| 50 | 0.079589 |
Общая формула для вероятности выигрыша w из n испытаний, где вероятность каждого выигрыша равна p, имеет вид combin(n,w) × p w × (1-p) (nw) = [n!/(w! × (nw)!] × p w × (1-p) (nw) .
Если я подброшу монету 1000 раз, какова вероятность того, что я увижу серию из как минимум 10 выпадений орла или решки подряд?
Забавно, что вы спросили; другой читатель только что прислал мне научную статью на эту тему. В этой статье есть следующий график, который показывает вероятность того, что она составит около 62%.
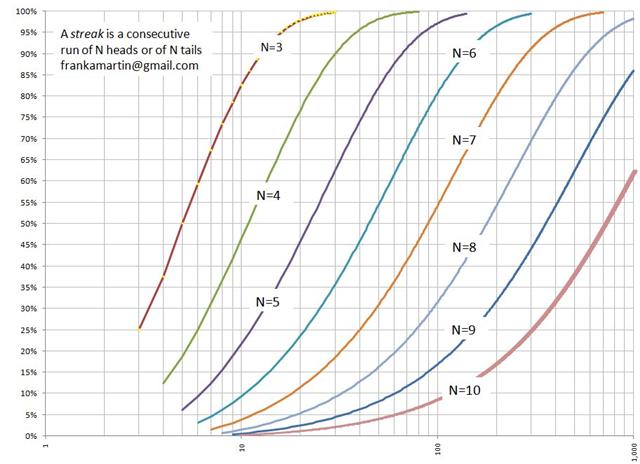
Для получения дополнительной информации по этой теме, пожалуйста, посетите статью Фрэнка Мартина «Какова была вероятность такой ужасной полосы неудач в казино?» (483K).
Если монету подбросить 100 раз, какова вероятность того, что хотя бы раз подряд выпадет не менее 7 орлов?
Если существует простое, нерекурсивное выражение для ответа, мне о нём неизвестно. Однако существует простое рекурсивное выражение для ответа.
f(n) = pr(решка при первом броске)×f(n-1) +
pr(орёл при первом броске, решка при втором броске)×f(n-2) +
pr(орёл в первых двух бросках, решка в третьем броске)×f(n-3) +
pr(орёл в первых трёх бросках, решка в третьем броске)×f(n-4) +
pr(орёл в первых 4 бросках, решка в четвёртом броске)×f(n-5) +
pr(орёл в первых 5 бросках, решка в пятом броске)×f(n-6) +
pr(орёл в первых 6 бросках, решка в шестом броске)×f(n-7) +
pr(орёл в первых 7 бросках) =
(1/2)×f(n-1) +
(1/2) 2 ×f(n-2) +
(1/2) 3 ×f(n-3) +
(1/2) 4 ×f(n-4) +
(1/2) 5 ×f(n-5) +
(1/2) 6 ×f(n-6) +
(1/2) 7 ×f(n-7) +
(1/2) 7
Где:
f(n) = вероятность успеха при n бросках.
pr(x) = вероятность наступления события x.
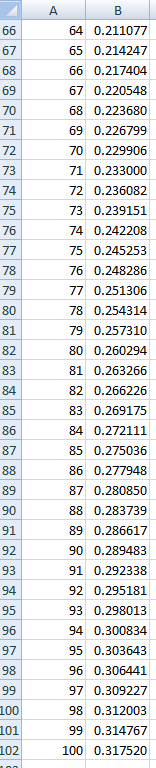
Электронные таблицы идеально подходят для решения подобных задач. На скриншотах таблицы ниже я указал вероятность 0 для ячеек B2–B8, потому что невозможно получить 7 орлов подряд за 6 или менее бросков. Для ячейки B9 я ввел формулу:
=(1/2)*B8+(1/2)^2*B7+(1/2)^3*B6+(1/2)^4*B5+(1/2)^5*B4+(1/2)^6*B3+(1/2)^7*B2+(1/2)^7
Затем я скопировал и вставил это из ячейки B10 в ячейку B102, что соответствует 100 броскам. Вероятность составляет 0,317520. Случайное моделирование это подтверждает.
 |  |
После первоначальной публикации Рик Перси поделился со мной своим решением задачи матричной алгебры. Вот оно, изложенное моими собственными словами. Я предполагаю, что читатель уже знаком с основами матричной алгебры.
Во-первых, в любой момент времени ласт может находиться в восьми различных состояниях:
p 1 = Вероятность успеха при условии, что вам нужно еще 7 орлов с текущей точки.
p 2 = Вероятность успеха при условии, что вам нужно еще 6 орлов с текущей точки.
p 3 = Вероятность успеха при условии, что вам нужно еще 5 орлов с текущей точки.
p 4 = Вероятность успеха при условии, что вам нужно еще 4 орла с текущей точки.
p 5 = Вероятность успеха при условии, что вам нужно еще 3 орла с текущей точки.
p 6 = Вероятность успеха при условии, что вам нужно еще 2 орла с текущей точки.
p 7 = Вероятность успеха при условии, что вам нужно еще 1 орёл с текущей точки.
p 8 = Вероятность успеха при условии, что вам больше не нужно выпадать орлом = 1.
Определим макстрикс S n как вероятность нахождения в каждом состоянии после n -го броска. S 0 представляет собой вероятности до первого броска, когда существует 100% вероятность нахождения в состоянии 0. Таким образом, S 0 =
| 1 0 0 0 0 0 0 0 |
Пусть T — матрица преобразования двух последовательных переворотов, или S n в S n+1 , где S n+1 = T × S n
- Если вы находитесь в состоянии 1, то после одного броска у вас есть 0,5 шанса оказаться в состоянии 2 (при выпадении орла) и 0,5 шанса остаться в состоянии 1 (при выпадении решки).
- Если вы находитесь во втором состоянии, то после одного броска у вас есть 0,5 шанса оказаться в третьем состоянии (при выпадении орла) и 0,5 шанса вернуться в первое состояние (при выпадении решки).
- Если вы находитесь в состоянии 3, то после одного броска у вас есть 0,5 шанса оказаться в состоянии 4 (при выпадении орла) и 0,5 шанса вернуться в состояние 1 (при выпадении решки).
- Если вы находитесь в состоянии 4, то после одного броска у вас есть 0,5 шанса оказаться в состоянии 5 (при выпадении орла) и 0,5 шанса вернуться в состояние 1 (при выпадении решки).
- Если вы находитесь в состоянии 5, то после одного броска у вас есть 0,5 шанса оказаться в состоянии 6 (при выпадении орла) и 0,5 шанса вернуться в состояние 1 (при выпадении решки).
- Если вы находитесь в состоянии 6, то после одного броска у вас есть 0,5 шанса оказаться в состоянии 7 (при выпадении орла) и 0,5 шанса вернуться в состояние 1 (при выпадении решки).
- Если вы находитесь в 7-м состоянии, то после одного броска у вас есть 0,5 шанса оказаться в 8-м состоянии (при выпадении орла) и 0,5 шанса вернуться в 1-е состояние (при выпадении решки).
- Если вы находитесь в состоянии 8, значит, вы добились успеха и останетесь в состоянии 8 с вероятностью 1,0.
Представим все это в виде матрицы перехода T =
| 0.5 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.5 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.5 0.0 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.5 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.5 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.5 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.5 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.5 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 |
Чтобы определить вероятность каждого состояния после одного броска...
(1) S 1 = S 0 × T
А что, если после двух переворотов?
(2) S 2 = S 1 × T
Подставим уравнение (1) в уравнение (2)...
(3) S 2 = S 0 × T × T = S 0 × T 2
А что будет после 3 переворотов?
(4) S 3 = S 2 × T
Подставляя уравнение (3) в (4)...
(5) S 3 = S 0 × T 2 × T = S 0 × T 3
Мы можем продолжать это делать вплоть до штата и после сотой попытки переворота...
S 100 = S 0 × T 100
Итак, что же такое T 100 ? До появления компьютеров, должно быть, было очень сложно разобраться в таких вещах. Однако, с помощью функции MMULT в Excel и множества операций копирования и вставки, мы получаем T 100 =
| 0.342616 0.171999 0.086347 0.043347 0.021761 0.010924 0.005484 0.317520 |
| 0.339863 0.170617 0.085653 0.042999 0.021586 0.010837 0.005440 0.323005 |
| 0.334379 0.167864 0.084271 0.042305 0.021238 0.010662 0.005352 0.333929 |
| 0.323454 0.162380 0.081517 0.040923 0.020544 0.010313 0.005178 0.355690 |
| 0.301693 0.151455 0.076033 0.038170 0.019162 0.009620 0.004829 0.399038 |
| 0.258346 0.129694 0.065109 0.032686 0.016409 0.008237 0.004135 0.485384 |
| 0.171999 0.086347 0.043347 0.021761 0.010924 0.005484 0.002753 0.657384 |
| 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 1.000000 |
Термин в правом верхнем углу показывает вероятность нахождения в состоянии 8 после 100 бросков, которая составляет 0,317520.
Слышали ли вы историю об австралийском игроке в крикет, который неправильно предсказывал результат подбрасывания монеты на протяжении 35 игр подряд, прежде чем сделать правильный ответ на 36-й раз? Какова вероятность такого исхода?
Я об этом не слышал, пока вы не упомянули. Вы имеете в виду удивительную историю юной крикетистки Кристи Перрин из команды «Магпайс», которая действительно 35 раз подряд неправильно угадала результат подбрасывания монеты. Вероятность получить ровно 35 или более неправильных результатов составляет (1/2) 35 = 1 к 34 359 738 368. Для сравнения, вероятность выигрыша в лотерею Powerball составляет 1 к 195 249 054. Это в 176 раз вероятнее, чем промахнуться 35 раз подряд при подбрасывании монеты.
У вас есть какие-нибудь советы по ставкам на подбрасывание монеты?
Да! Ставьте на сторону, лежащую в руке подбрасывающего монету. В научной статье «Динамическая предвзятость при подбрасывании монеты» Перси Диаконис, Сьюзан Холмс и Ричард Монтгомери делается вывод, что монета упадет на ту же сторону, с которой начала падение, в 51% случаев.
Этот вопрос был поднят и обсужден на форуме моего дочернего сайта Wizard of Vegas .
В среднем, сколько попыток потребуется в игре с равными шансами (50/50), чтобы проиграть две игры подряд? А если 3, 4, n подряд?
Давайте сначала решим задачу для случая с двумя убытками.
Пусть x — ожидаемое количество будущих бросков кубиков, начиная с самого начала или после любой выигрышной комбинации.
Пусть y — ожидаемое количество будущих переворотов после одного проигрыша.
Мы можем составить следующие два уравнения:
(1) x = 1 + 0,5x + 0,5y
Первый вариант означает, что игрок должен подбросить монету, чтобы изменить состояние. Вероятность выигрыша составляет 50%, игрок остаётся в состоянии x. Вероятность проигрыша составляет 50%, игрок переходит в состояние y.
(2) y = 1 + 0,5x
Снова из состояния y, 1 обозначает бросок в этот момент. Существует 50% вероятность выигрыша, что приводит к возвращению в состояние x. Существует 50% вероятность проигрыша, что завершает игру и не требует дополнительных бросков, поэтому подразумевается 0,5*0.
Умножьте оба уравнения на 2 и переставьте их местами, чтобы получить:
(3) x - y =2
(4) -x + 2y = 2
Сложите два уравнения, чтобы получить:
(5) y = 4
Подставьте это в любое уравнение от (1) до (4) и получите x=6.
В случае трех потерь определим три возможных состояния следующим образом:
Пусть x — ожидаемое количество будущих бросков кубиков, начиная с самого начала или после любой выигрышной комбинации.
Пусть y — ожидаемое количество будущих переворотов после одного проигрыша.
Пусть z — ожидаемое количество будущих переворотов после двух проигрышей.
Исходные уравнения следующие:
x = 1 + 0,5x + 0,5y
y = 1 + 0,5x + 0,5z
z = 1 + 0,5x
Начальные состояния можно представить в матричной форме следующим образом:
| 0,5 | -0.5 | 0 | 1 |
| -0.5 | 1 | -0.5 | 1 |
| -0.5 | 0 | 1 | 1 |
Если вы помните матричную алгебру, мы можем решить уравнение относительно x как determinant(A)/determinant(B), где
А =
| 1 | -0.5 | 0 |
| 1 | 1 | -0.5 |
| 1 | 0 | 1 |
Б =
| 0,5 | -0.5 | 0 |
| -0.5 | 1 | -0.5 |
| -0.5 | 0 | 1 |
| 0,5 | -0.5 | 0 |
| -0.5 | 1 | -0.5 |
| -0.5 | 0 | 1 |
В Excel есть удобная функция определения: =mdeterm(диапазон). В данном случае x = mdeterm(матрица A)/mdeterm(матрица B) = 1,75/0,125 = 14.
Для дополнительных последовательных проигрышей мы можем использовать рекурсию. Рассмотрим число 4. Из вышеизложенного мы знаем, что в среднем потребуется 14 подбрасываний монеты, чтобы получить 3 проигрыша подряд. В этот момент монета будет подброшена снова, с 50% вероятностью начала заново. Итак:
x = 14 + 1 + x/2
x/2 = 15
x = 30
Иными словами, прибавьте единицу к предыдущему ответу, а затем удвойте его.
Заметить закономерность несложно. Ожидаемое количество бросков, необходимых для получения n проигрышей подряд, равно 2n+1-2 .
Этот вопрос был поднят и обсужден на моём форуме, посвящённом игре Wizard of Vegas .
Если честная монета подбрасывается n раз, какова вероятность того, что хотя бы один раз выпадет t решек подряд?
Ответ равен 1-F (t) n+2 / 2n , где F (t) n — n-е число в последовательности Фибоначчи из t шагов.
Что такое последовательность Фибоначчи, спросите вы? Первое число — единица. В последовательности из t шагов каждое последующее число является суммой предыдущих t чисел. Предположим, что любое число перед первым числом равно нулю.
Рассмотрим последовательность из двух шагов. Первое число — 1. Второе — сумма двух предыдущих чисел. Предположим, перед единицей стоит ноль, тогда второе число — 0+1=1. Третье число — 1+1=2, четвёртое — 1+2=3, пятое — 2+3=5.
Первые двенадцать чисел Фибоначчи, вычисленных в два шага, это: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144.
Давайте рассмотрим пример. Какова вероятность того, что хотя бы раз из десяти бросков выпадут две решки подряд?
Мы используем двухшаговую последовательность Фибоначчи, потому что нам нужно всего два хвоста. 12-е число в последовательности (на два больше, чем количество подбрасываний) равно 144. Таким образом, ответ 1-F (2) 10+2 /2 10 = 1 - 144/2 10 = 1 - 144/1024 = 85,94%.
А какова вероятность выпадения пяти решек подряд из 20 бросков?
Первые 22 числа Фибоначчи, состоящие из 5 шагов, это 1, 1, 2, 4, 8, 16, 31, 61, 120, 236, 464, 912, 1793, 3525, 6930, 13624, 26784, 52656, 103519, 203513, 400096, 786568.
Таким образом, ответ равен 1 - F (5) 20+2 /2 20 = 1 - 786,568/1,048,576 = 1 - 75,01% = 24,99%.
Этот вопрос обсуждается на моём форуме, посвящённом игре Wizard of Vegas .
Есть смещенная монета, вероятность выпадения орла на которой составляет 60%. Ее подбрасывают до тех пор, пока не выпадут два орла или две решки подряд. Какова вероятность того, что сначала выпадут два орла?
Вот ответ и решение (PDF).
Для обсуждения этой проблемы, пожалуйста, посетите мой форум на сайте Wizard of Vegas .
Волшебник, я вызываю тебя на пари. Вот правила:
- Вы можете выбрать любой понравившийся вам вариант выпадения орла (H) и решки (T). Например, HTT.
- После того, как я покажу вам ваш узор, я выберу свой.
- Мы будем подбрасывать монету снова и снова, пока не выпадет один из возможных вариантов. Побеждает тот, кто выберет этот вариант.
- Я дам вам коэффициент 3 к 2.
Вы согласны? Я буду делать это столько раз, сколько вы пожелаете.
Нет. Хорошая попытка, однако. У игрока, действующего вторым, огромное позиционное преимущество. Вот стратегия для игрока, действующего вторым, и его вероятность победы.
Стратегия игры Одиусгамбит
| Игрок 1 | Игрок 2 | Игрок №2 побеждает |
|---|---|---|
| ХХХ | ТХХ | 87,50% |
| ХХТ | ТХХ | 75,00% |
| СПАСИБО | ХХТ | 66,67% |
| ХХТ | ТХХ | 75,00% |
| ТХХ | ХТТ | 75,00% |
| ТХТ | ТТХ | 66,67% |
| ТТХ | ХТТ | 75,00% |
| ТТТ | ХТТ | 87,50% |
Как показывает таблица выше, мой лучший шанс на победу, или ваш наименьший, — это если я выберу либо THT, либо HTH, где мой шанс на победу все равно составляет всего 1 к 3. Для честной ставки мне нужно получить 2 к 1, поэтому, получив 3 к 2, вы получаете преимущество в 16,67%.
Вот как запомнить стратегию второго игрока. Пусть P(x) — выбор первого игрока на позицию x. Пусть O(x) — противоположный выбор первого игрока на позицию x. Второй игрок всегда должен выбирать: O(2) - P(1) - P(2).
Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .
Если подбросить честную монету 40 раз, какова вероятность получить как серию из 5 орлов, так и серию из 5 решек? «Серия» означает как минимум 1 выпадение, а «5» — как минимум 5. Серии с орлом и решкой не обязательно должны быть смежными.
Пожалуйста, нажмите на кнопку ниже, чтобы получить ответ.
Вот моё решение (PDF).
Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .
Генри и Том решают поспорить на подбрасывание монеты. Генри выигрывает, если выпадает орёл, Том выигрывает, если выпадает решка.
Ставка составляет 1 доллар за каждый бросок, и им ужасно скучно, поэтому они решают сделать миллион бросков. В конце сессии проигравший выпишет победителю чек на итоговую сумму. Какова ожидаемая стоимость суммы чека?
Общая формула для ответа: sqrt(дисперсия * (2/pi)).
В данном случае дисперсия составляет 1 000 000. Таким образом, ожидаемая абсолютная разница между фактическим и ожидаемым результатом равна sqrt(1 000 000 × (2/π)) ≈ 797,88456080286535587989211986876373695171726 232986931533185165934131585179860367700250466 781461387286060511772527036537102198390911167 448599242546125101541269054116544099863512903 269161506119450728546416733918695654340599837 28381269120656178667772134093073.
Я задаю похожий вопрос в рубрике «Спроси у мастера» № 358 , который поможет показать, откуда я взял член sqrt(2/pi).
[/спойлер]Этот вопрос был задан и обсуждался на форуме Wizard of Vegas .
Предположим, в казино есть игра, основанная на честном подбрасывании монеты, с выплатой равных денег. Игрок хочет сыграть миллион раз, делая ставку в 1 доллар за раз. Сколько денег он должен внести, чтобы иметь 50% шанс не разориться?
Давайте сначала ответим на вопрос о том, какова вероятность того, что игрок окажется в минусе более чем на x единиц после миллиона бросков, при условии, что у игрока неограниченный банкролл.
Поскольку это честная ставка, средний выигрыш после миллиона бросков равен нулю. Дисперсия каждого броска равна 1, поэтому дисперсия одного миллиона бросков равна одному миллиону. Таким образом, одно стандартное отклонение равно sqrt(1 000 000) = 1000.
Необходимый банкролл можно рассчитать с помощью функции Excel =norm.inv(вероятность, среднее значение, стандартное отклонение). Например, если ввести =norm.inv(.25,0,1000), получим -674,49. Это означает, что после миллиона бросков у игрока есть 25% шанс проиграть 674 или больше. Обратите внимание, что это приблизительная оценка. Для получения точного ответа следует использовать биномиальное распределение, что было бы очень трудоемко при миллионе бросков.
Вполне возможно, что если игрок взял на кон 674 доллара, то может остаться без денег до того, как выпадет миллион. Если же он сможет продолжать играть в кредит, то, возможно, ему удастся отыграться и закончить игру с убытком менее 674 долларов. Фактически, как только игрок окажется в минусе (-674), существует 50/50 вероятность, что в любой момент в будущем его баланс окажется выше или ниже -674.
Таким образом, если игрок может играть в кредит, возможны три варианта развития событий.
- Игрок никогда не опускается ниже -674.
- В какой-то момент игрок опускается ниже отметки -674, но затем восстанавливается и завершает игру с результатом выше -674.
- В какой-то момент игрок опускается ниже отметки -674, продолжает играть и проигрывает еще больше.
Мы установили, что вероятность сценария 3 составляет 25%.
Вероятность второго сценария должна быть такой же, как и у третьего, потому что, как только игрок окажется в минусе -674, у него есть 50/50 шанс закончить игру выше или ниже этого значения после миллиона бросков.
Сценарий 1 — единственная альтернатива, вероятность которой должна составлять 100%-25%-25% = 50%.
Если вероятность того, что игрок никогда не опустится ниже 674, составляет 50%, то вероятность того, что он опустится ниже 674, должна составлять 100% - 50% = 50%.
Итак, вот ответ на первоначальный вопрос: 674 доллара.
Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .


