WOO logo

Wizard рекомендует

Вероятность - Кубики

Если вы бросаете 6 стандартных шестигранных игральных костей, какова вероятность того, что выпадет шесть одинаковых кубиков?

Jeff B. от Miami, Florida

Ответ: 6*(1/6) 6 = 6/46 656 = 1/7 776 ≈ 0,0001286.
Каково среднее количество бросков до того, как игрок «выбьет семерку»? Я знаю, что семерка выпадает каждые 6 бросков, но с учетом возможности получения нескольких очков в крэпсе и 7-11, я думаю, что среднее количество бросков может быть выше, чем ожидалось. Существуют ли какие-либо математические справочные материалы по этому вопросу?

Grshooter от Kansas City, Missouri

Среднее количество бросков на одного игрока составляет 8,525510. Вероятность выпадения ровно 2 бросков до 200 бросков можно посмотреть на моей странице, посвященной вероятности выживания в крэпсе .
Каковы шансы (и частота) проигрыша ставки DP при 100 000 бросках игральных костей (крэпс/линия «не пас») 2 раза, 3 раза, 4 раза, 5 раз, 6 раз, 7 раз, 8 раз или 9 раз подряд?

Derick от Minneapolis, USA

В моем приложении по игре в кости показано, как рассчитать шансы для любой отдельной ставки. Там вы увидите, что вероятность проигрыша ставки «не пас» составляет 2928/5940. Вероятность проигрыша n ставок подряд равна (2928/5940) n . Частоту проигрыша ровно n раз из 100 000 можно приблизительно оценить как 100 000 * (2928/5940) n+2 .
Какова вероятность выпадения одного и того же числа при одном броске шести игральных костей?

Kyle Hill от Colstrip, Montana

Вероятность выпадения шести одинаковых чисел на шести игральных костях составляет 6*(1/6) 6 = 1/7776 ≈ 0,01286%.
Как часто можно бросить пару игральных костей 28 раз, не получив 7? Как вы это вычислили? Поздравляю с вашим сайтом, он замечательный.

Arturo G. от Mexico City, Mexico

Спасибо за комплимент. Я так понимаю, вы имеете в виду вероятность того, что пара игральных костей выпадет 28 раз без семерки? Вероятность того, что семерка не выпадет ни при одном броске, составляет 5/6. Вероятность того, что семерка не выпадет за 28 бросков, равна (5/6) ²⁸ = 0,006066, или примерно 1 к 165.
Вопрос по восточной игре в кости, где игроки должны угадать, какая сторона кубика выпадет. Сначала игроки делают ставки на 1, 2, 3, 4, 5, 6 (как в рулетке), а затем «дилер» одновременно бросает 3 кубика. Выплаты составляют 1:1, если выбранное число выпадает один раз (на любом из 3 кубиков), 2:1, если выбранное число выпадает дважды, и 3:1, если выбранное число выпадает на всех 3 кубиках. Поскольку игрок может сделать любое количество ставок на игровом поле, какое будет оптимальное количество ставок? (при условии, что все мои ставки равны по размеру)

Jansen от Toronto, Canada

Вероятность совпадения трех чисел составляет 1/216. Вероятность совпадения двух чисел составляет 3*5/216. Вероятность совпадения одного числа составляет 25*5/216. Вероятность отсутствия совпадений составляет 5*5*5/216. Таким образом, ожидаемая прибыль составляет 3*(1/216)+2*(15/216)+1*(75/216)-1*(125/216)=-17/216=-7,87%. Оптимального количества ставок не существует, вы потеряете ожидаемые 7,87% от общей суммы поставленных денег независимо от того, что вы делаете.

Эти ставки можно делать как в сик бо , так и в чак а лак .
Уважаемый господин Волшебник, какова вероятность выпадения двух пар при броске четырех игральных костей?

Brian от St. Catherines, Canada

Существует 15 возможных комбинаций пар (6,2). Существует 6 способов выпадения любых двух пар на кубиках. Всего существует 6^4 = 1296 способов выпадения четырех кубиков. Таким образом, вероятность составляет 90/1296 = 6,9444%.
Если я бросаю игральную кость, вероятность выпадения шестерки составляет 1/6. Если я бросаю две игральные кости, увеличивается ли вероятность выпадения шестерки на одной из них, или она остается на уровне 1/6?

Mike R. от Rosemount

Если вы бросили x кубиков, вероятность выпадения хотя бы одной шестерки составляет 1-(5/6) ² . В случае двух кубиков эта вероятность равна 30,56%.
Сколько существует различных способов выбросить 3 единицы, используя 6 игральных костей?

Jamie от Croydon, England

Во-первых, существует 20 способов выбрать три единицы из 6 возможных, используя функцию комбинации (6,3). Затем каждая из оставшихся трех единиц может выпадать из пяти возможных чисел. Таким образом, общее количество способов составляет 20 × 5 × 3 = 2500. Общее количество способов бросить все кости равно 6 × 6 = 46 656, поэтому вероятность выпадения ровно трех единиц равна 2500/46656 = 0,0536. Для получения помощи по функции комбинации см. мой раздел о вероятностях в покере .
Какова вероятность того, что на одной из трех игральных костей выпадет ОДИН знак, если бросить их одновременно? Насколько я понимаю, вероятность должна быть 50% (1/6 + 1/6 + 1/6 = 1/2 --> 50%). Но в вашей таблице вероятностей указано 34,72%. Пожалуйста, помогите.

John C. от Singapore

Вероятность выпадения ровно одной единицы на трех кубиках составляет 3*(5/6) 2 *(1/6) = 75/216 = 34,72%.
Какова вероятность выпадения «пары» при броске 4 игральных костей?

Anthony от Toronto, Canada

Пара может состоять из любого из 6 чисел. Два других числа могут быть из остальных пяти. Таким образом, уже существует 6*комбинаций(5,2)=60 комбинаций. Существует комбинаций(4,2)=6 комбинаций игральных костей, на которых может появиться пара. Два числа могут быть расположены двумя способами. Таким образом, существует 60*12=720 способов выбросить пару. Общее количество способов выбросить кости равно 64 =1296. Следовательно, вероятность составляет 720/1296 ≈ 55,56%.
Мой друг владеет баром, и у них есть «коктейль дня», для приготовления которого в контейнере Tupperware лежат десять игральных костей. Какова вероятность того, что в одном коктейле выпадут 8 одинаковых костей из 10? Спасибо за ваше время.

August от Oshkosh, USA

Вероятность того, что при броске 10 кубиков выпадут ровно 8 одинаковых чисел, равна 6*combin(10,8)*(1/6) 8 *(5/6) 2 = 1/8957,952. Вероятность совпадения хотя бы 8 чисел равна 6*[combin(10,8)*(1/6) 8 *(5/6) 2 + combin(10,9)*(1/6) 9 *(5/6) + (1/6) 10 ] = 1/8569,469.
Недавно во время игры в нарды мне четыре раза подряд выпали две шестерки. Какова вероятность того, что это повторится?

David от Sunland, USA

При каждом новом броске вероятность того, что следующие четыре броска будут состоять из двух шестерок, составляет (1/36) 4 = 1 из 1679616.
Какова вероятность получить стрит при одном броске пяти игральных костей?

Teodoro C. Deocares от Dagupan, Philippines

Существует два возможных варианта расположения чисел: от 1 до 5 и от 2 до 6. Каждый из этих вариантов можно упорядочить 5! = 120 способами. Существует 6 5 = 7776 способов бросить пять кубиков. Таким образом, вероятность составляет 2*120/7776 = 3,09%. Вероятность этого кажется намного выше сразу после того, как я поставил отметку 0 для большого стрита во время игры в Ятзи.
Игральная кость с честными сторонами бросается 30 раз. Каково ожидаемое количество выпадений числа 1? Какова вероятность того, что число 1 выпадет ожидаемое количество раз?

анонимный

Ожидаемое количество единиц равно 30*(1/6) = 5. Вероятность выпадения ровно 5 единиц равна combin(30,5)*(1/6) 5 *(5/6) 25 = 19,21%.
Если у меня есть любое заданное количество игральных костей, какова вероятность того, что при броске всех костей хотя бы одна из них выпадет на единицу?

анонимный

Вероятность того, что на всех кубиках выпадет не единица, равна (5/6) n . Следовательно, вероятность выпадения хотя бы одной единицы равна 1-(5/6) n . Рассмотрим пример с пятью кубиками. Ответ будет 1-(5/6) n = 59,81%.
Если я брошу 36 игральных костей, какова вероятность того, что выпадет хотя бы одна шестерка?

анонимный

1-(5/6) 36 = 99,86%
Если бы я продолжал бросать кубики, каждый раз убирая все шестерки, как бы я мог предсказать теоретическое количество кубиков, оставшихся после определенного количества бросков?

анонимный

Ожидается, что при каждом броске останется 5/6 кубиков. Таким образом, ожидаемое количество кубиков, оставшихся после n бросков, составит 36*(5/6) n . Например, после 10 бросков в среднем останется 5,81 кубика.
Если я брошу три игральные кости, какова вероятность того, что хотя бы два числа окажутся одинаковыми?

анонимный

Вероятность того, что все числа будут разными, составляет (5/6)*(4/6)=20/36. Следовательно, вероятность того, что хотя бы два числа будут одинаковыми, равна 1-(20/36) = 16/36 = 44,44%.
Если два человека бросают пару игральных костей, какова вероятность того, что выпадет одно и то же число? Существует ли формула для вычисления этого?

анонимный

Да. Просто переберите все числа от 2 до 12 и определите вероятность выпадения каждого из них дважды. Таким образом, ответ будет (1/36) ² + (2/36) ² + (3/36) ² + (4/36) ² + (5/36) ² + (6/36) ² + (5/36) ² + (4/36) ² + (3/36) ² + (2/36) ² + (1/36) ² = 11,27%.
Недавно я был на больничном празднике. В качестве приза разыгрывался новый автомобиль, если на 7 игральных костях выпадет 7 шестерок за один бросок. Стоимость участия — 1 фунт стерлингов. Шансы на выигрыш, должно быть, высоки, но насколько?

анонимный

Вероятность выпадения семи шестерок на семи игральных костях составляет (1/6) 7 = 1 к 279 936. Таким образом, чтобы ставка была выгодной, автомобиль должен стоить 279 936 фунтов стерлингов или больше. Даже средний Rolls Royce столько не стоит, поэтому я бы сказал, что это ужасная ставка.

[Bluejay добавляет: Да, конечно, но, думаю, суть в том, что это было благотворительно. Что интереснее: пожертвовать 1 фунт стерлингов на благотворительность и не получить ничего взамен, кроме приятного чувства помощи, или пожертвовать 1 фунт стерлингов и получить приятное чувство плюс небольшой шанс выиграть машину?]

Каковы вероятности выпадения пяти одинаковых карт, четырех одинаковых карт, трех одинаковых карт, фулл-хауса, двух пар, пары, стрита и ничего при броске пяти игральных костей?

анонимный

  • Пять одинаковых чисел: 6/6 5 = 0,08% (очевидно)
  • Четыре одинаковых символа: 5*6*5 = 1,93% (пять возможных позиций для одного символа * 6 рангов для четырех одинаковых символов * 5 рангов для одного символа).
  • Фулл-хаус: combin(5,3)*6*5/6 5 = 3,86% (комбинация(5,3) позиций для тройки * 6 рангов для тройки * 2 ранга для пары).
  • Три одинаковых числа: COMBIN(5,3)*COMBIN(2,1)*6*COMBIN(5,2) / 6 5 = 15,43%. (позиции COMBIN(5,3) для трех одинаковых чисел * позиции COMBIN(2,1) для большего из отдельных чисел * 6 рангов трех одинаковых чисел * ранги COMBIN(5,2) для двух отдельных чисел.
  • Две пары: COMBIN(5,2)*COMBIN(3,2)*COMBIN(6,2)*4 / 6 5 = 23,15% (позиции COMBIN(5,2) для старшей пары * позиции COMBIN(3,2) для младшей пары * ранги COMBIN(6,4) для двух пар * 4 ранга для одиночного элемента.
  • Пара: COMBIN(5,2)*fact(3)*6*combin(5,3) / 6 5 = 46,30% (позиции COMBIN(5,2) для пары * позиции Fact(3) для трех отдельных элементов * 6 рангов для пары * ранги COMBIN(5,3) для отдельных элементов.
  • Прямой порядок: 2*факт(5) / 6 5 = 3,09% (2 варианта для прямого порядка {1-5 или 2-6} * факт(5) способов расположить элементы в порядке).
  • Ничего: ((COMBIN(6,5)-2)*FACT(5)) / 6 5 = 6,17% (combin(6,5) способов выбрать 5 рангов из шести, минус 2 для прямых, * fact(5) способов расположить в порядке.
Привет, Волшебник! Хотел бы узнать, можешь ли ты ответить на этот вопрос. В популярной азартной игре во Франции XVII века игрок бросал пару игральных костей 24 раза. Он выигрывал, если хотя бы один из бросков выпадал двойной шестеркой. В то время велись споры о том, была ли вероятность выигрыша выше или ниже 50%. Можешь мне помочь?

анонимный

Конечно, это просто. Вероятность выпадения хотя бы одной двенадцатки из 24 бросков составляет 1-(35/36) 24 = 49,14%. Таким образом, шансы склоняются в пользу ставки против двенадцатки. Это умная ставка, потому что ожидаемое количество двенадцаток из 24 бросков составляет 2/3. Однако это не означает, что вероятность выпадения двенадцатки равна 2/3, потому что иногда выпадает больше одной двенадцатки, и игрок, ставящий на двенадцатку, не выигрывает больше, если выпадет дополнительная двенадцатка после первой. Если вероятность выигрыша в любом данном испытании равна p, количество испытаний равно n, а вероятность хотя бы одного выигрыша равна w, то, выразив p и w через n, мы получаем...

w=1-(1-p) n
1-w = (1-p) n
log(1-w) = log((1-p) n )
log(1-w) = n*log(1-p)
n = log(1-w)/log(1-p)

В вашем примере n = log(1-.5) / log(1-(1/36)) = log(0.5) / log(35/36) = 24.6051. Таким образом, если вероятность успеха составляет 50% при 24,6 бросках, то при 24 бросках она должна быть немного меньше.

Какова вероятность того, что при броске шести игральных костей шесть раз подряд выпадут числа 1, 2, 3, 4, 5, 6?

анонимный

Вероятность выпадения числа 123456 шестью кубиками за один бросок можно выразить как: вероятность (второй кубик не совпадает с первым) * вероятность (третий кубик не совпадает с первым или вторым) * ... = 1 * (5/6) * (4/6) * (3/6) * (2/6) * (1/6) = 0,015432. Таким образом, вероятность повторения этого события шесть раз подряд составляет 0,015432 / 6 = 1 из 74 037 208 411.
Если я бросаю одну игральную кость 6 раз, какова вероятность того, что ровно 4 раза выпадет «2»?

анонимный

Combine(6,2)*(1/6) 4 *(5/6) 2 = 0.008037551.
Какова вероятность выпадения числа 13 или больше при броске 3, 4 и 5 кубиков, если разрешено оставлять себе три кубика с наивысшими значениями?

анонимный

Вот вероятности:

3 кубика: 25,93%
4 кубика: 48,77%
5 кубиков: 66,13%.

Предположим, мы бросаем три честные шестигранные игральные кости. Какова условная вероятность того, что на первой кости выпадет 4, при условии, что сумма выпавших чисел равна 12?

Shikha от North Ryde

Вероятность выпадения A при условии выпадения B равна вероятности выпадения A и B, деленной на вероятность выпадения B. В данном случае вероятность выпадения 4 на первой кости и затем 8 на двух других составляет (1/6) * (5/36) = 5/216. Вероятность выпадения любой суммы 12 на трех костях составляет 25/216, как показано в моем разделе по сик-бо . Таким образом, ответ равен (5/216) / (25/216) = 5/25 = 20%.
В недавнем упражнении по программированию мне и другим студентам было предложено описать шестигранную игральную кость в коде, а затем использовать эти кости для определения простой игры. Цель игры заключалась в том, чтобы бросать кости до тех пор, пока сумма бросков не достигнет ровно 100. Любые броски, сумма которых превышала 100, не суммировались, а просто добавлялись к статистике. Быстро выяснилось, что 17 бросков — это минимальное количество бросков, необходимое для достижения 100. Однако вычисление вероятности этого оказалось сложной задачей. Вычисление вероятности определенной последовательности бросков довольно просто, но как учесть как неспецифический порядок бросков, так и различные способы достижения 100 за 17 бросков (16*6 + 1*4 и 15*6 + 2*5)?

Björn от Göteborg, Sweden

Упомянутые вами два способа — единственные способы выбросить в сумме 100 очков за 17 бросков. Вероятность выбросить 16 шестерок и одну четверку составляет 17*(1/6) ¹⁷ . Существует 17 возможных позиций для 4, и каждая последовательность имеет вероятность (1/6)*(1/6)*...*(1/6) с 17 членами. Количество способов получить 15 шестерок и 2 пятерки — это комбинация (17,2) = 136. Таким образом, вероятность 15 шестерок и 2 пятерок составляет 136*(1/6) ¹⁷ . Следовательно, общая вероятность равна (17+136)*(1/6) ¹⁷ = 1 из 110 631 761 077.
Есть 3 игральные кости: 2 шестигранные и одна, на всех гранях которой выпала шестерка. Все кости лежат у меня в кармане. Я наугад достаю одну из костей и бросаю её. Выпадает шестерка. Какова вероятность того, что это была одна из шестигранных костей с шестью различными значениями?

Annojh от Toronto

Пусть A = Выбор обычной игральной кости
Пусть B = выпадение шестерки при броске случайно выбранной игральной кости.
Ответ = Pr(A при условии B) = Pr(A и B)/pr(B) = ((2/3)*(1/6))/((2/3)*(1/6)+(1/3)*1) = (2/18)/((2/18)+(6/18)) = 1/4.
Если шесть игральных костей можно бросить только один раз, какова вероятность выпадения чисел 6, 6, 6, 6, 1 и 4 в любом порядке?

Aubrey от Kokomo

Существует 6!/(4!*1!*1!) = 30 способов расположить эти числа в любом порядке. Другими словами, есть 6 позиций для размещения 1 и 5 для размещения 4, поэтому 6*5=30. Вероятность получить 666614 именно в таком порядке составляет 1 из 6 = 1 из 46656. Умножим это на 30 для 30 возможных порядков, и получим 30/46656 = 0,0643%, или 1 из 1552,2.
В моем понимании «время ожидания» события — это величина, обратная вероятности этого события. Меня интересует расчет времени ожидания до выпадения двух подряд выпавших чисел на одной игральной кости. В симуляции я получаю в среднем 42 броска. Как мне установить связь с вероятностью выпадения двух подряд выпавших чисел?

Lee от Andover

Действительно, для одиночных событий, если вероятность равна p, то среднее время ожидания составляет 1/p. Однако с последовательными событиями ситуация усложняется. Пусть x — состояние, в котором последний бросок не выпал на двойку. Это также состояние в начале. Пусть y — состояние, в котором последний бросок выпал на двойку. После первого броска вероятность того, что мы останемся в состоянии x, составляет 5/6, а вероятность того, что мы останемся в состоянии y, — 1/6. Пусть Ex(x) — ожидаемое количество бросков из состояния x, а Ex(y) — ожидаемое количество из состояния y. Тогда...

Ex(x) = 1 + (5/6)*ex(x) + (1/6)*ex(y), и
Ex(y) = 1 + (5/6)*ex(x)

Решая эти два уравнения...

Ex(x) = 1 + (5/6)*ex(x) + (1/6)*( 1 + (5/6)*Ex(x))
Ex(x) = 7/6 + (35/36)*Ex(x)
(1/36)*Ex(x) = 7/6
Ex(x) = 36*(7/6) = 42

Таким образом, среднее время ожидания двух последовательных двоек составляет 42 броска кубика.

У меня похожая проблема, только для получения двух орлов нужны ожидаемые подбрасывания кубика. На моем сайте с математическими задачами , смотрите задачу 128.

Можете ли вы сказать мне вероятность выпадения двух одинаковых чисел на двух, трёх и четырёх игральных костях? Меня интересует, сколько игральных костей нужно бросить за один раз, чтобы вероятность была на стороне бросающего кости. (Не имеет значения, какое число удвоится.)

Mary от Minneapolis, MN

Вот вероятность выпадения хотя бы одного числа более одного раза в зависимости от количества бросков:

Вероятность наличия пары или более

Роллы Вероятность
2 рулона 16,67%
3 рулона 44,44%
4 рулона 72,22%
5 рулонов 90,74%
6 рулонов 98,46%

Таким образом, если вы собираетесь забронировать это блюдо, вы должны ответить «да» при заказе 3 роллов или «нет» при заказе 4 роллов.
Какова вероятность получить сумму больше 100 при броске 20 игральных костей? С уважением.

Terje от Stockholm

Я начал использовать нормальное приближение для решения этой задачи, но вероятность получения более 100 точек слишком низка, чтобы этот метод был точным. Поэтому я провел случайное моделирование 8,25 миллионов испытаний, и количество испытаний, в которых было 101 точка или больше, составило 127. Таким образом, вероятность составляет примерно 1 к 65 000.
Волшебник, не могли бы вы описать эквивалентные шансы в лотерее California SuperLotto Plus (1 к 41,4 миллионам) в терминах количества последовательных выпадений 7 или 11? Я где-то это слышал. Большинство людей не могут понять вероятности в лотерее. Но вот бросок игральных костей — они могут это понять.

Tim от Belmont, CA

Пусть n — ваш ответ. Вероятность выпадения 7 или 11 составляет 8/36. Чтобы найти n:

(8/36) n = 1/41 400 000

log((8/36) n ) = log(1/41,400,000)

n × log(8/36) = log(1/41,400,000)

n = log(1/41 400 000)/log(8/36)

n = -7,617 / -0,65321

n = 11,6608

Итак, вероятность выигрыша в SuperLotto такая же, как при выпадении семерки или одиннадцати чисел 11,66 раз подряд. Для тех, кто не понимает, что такое частичный бросок, я бы перефразировал: вероятность составляет от 11 до 12 последовательных бросков.

У нас возник спор между работниками. В баре неподалеку есть игра «Встряхивание». Нужно бросить пять кубиков одновременно, и все пять должны выпасть одинаково, как в ятзи, но с тремя попытками. При этом нужно трижды поднять все выпавшие кубики. Вопрос в том, какова вероятность выпадения одинакового числа за один раз и какова вероятность выпадения одинакового числа за три разрешенных броска. Спасибо, если вы уже отвечали на этот вопрос, извините, но я не смог найти ответ.

Dan and co workers at maple island от Forest Lake

Вероятность выпадения пяти одинаковых чисел за один бросок составляет 6 * (1/6) ·5 = 1/1296. Это потому, что существует шесть различных пяти одинаковых чисел (от одного до шести), и вероятность того, что на каждой игральной кости выпадет именно это число, равна (1/6). Вероятность не получить пять одинаковых чисел составляет 1 - (1/1296) = 1295/1296. Вероятность трех попыток без трех одинаковых чисел составляет (1295/1296) ·3 = 99,77%. Таким образом, вероятность получить хотя бы одну пятерку одинаковых чисел за три попытки составляет 100% - 99,77% = 0,23%.
Каково ожидаемое количество бросков, необходимых для получения хотя бы одного из каждого из возможных результатов на непредвзятой шестигранной игральной кости?

Michael от Melbourne

Если вероятность чего-либо равна p, то в среднем потребуется 1/p испытаний, чтобы это произошло в первый раз. Очевидно, что при первом броске вы вычеркнете одно число. Вероятность выпадения одного из пяти других чисел в следующий раз составляет 5/6. Таким образом, в среднем потребуется 1/(5/6) = 6/5 = 1,2 броска, чтобы это произошло. Следуя этим рассуждениям, ожидаемое количество бросков составляет (6/6) + (6/5) + (6/4) + (6/3) + (6/2) + (6/1) = 14,7.
Какова классическая вероятность выпадения числа 12 при броске 5 сбалансированных игральных костей?

Kennith H. от Winters

Надеюсь, вы довольны, я только что добавил новый раздел с ответами на подобные вопросы для игральных костей от 1 до 25. Как показывает таблица для пяти игральных костей, вероятность выпадения суммы 12 составляет 0,039223251028807.

Если бросать две игральные кости снова и снова, пока не произойдет одно из следующих событий, то какое из них с большей вероятностью произойдет первым:

  • Выпадают числа шесть и восемь, в любом порядке, допускаются дубликаты.
  • Число семь выпадает дважды.

Мне предложили пари, что первыми выпадут шестерка и восьмерка. Я согласился, потому что семь — наиболее вероятная сумма. Однако, повторяя это снова и снова, я проиграл 2500 долларов. Каковы шансы?

Anthony от Indiana

Боюсь, вы выбрали квадратную сторону этой ставки. Вероятность выпадения двух семерок до шестерки и восьмерки составляет 45,44%. Вот все возможные исходы. В первом столбце указан порядок бросков кубиков, приведших к результату ставки, без учета всех остальных.

Две семерки перед ставкой на шесть и восемь

Соответствующие свитки Вероятность Формула Исход
6,8 0.142045 (5/16)*(5/11) Терять
8,6 0.142045 (5/16)*(5/11) Терять
6,7,8 0.077479 (5/16)*(6/11)*(5/11) Терять
7,6,8 0.053267 (6/16)*(5/16)*(5/11) Терять
8,7,6 0.077479 (5/16)*(6/11)*(5/11) Терять
7,8,6 0.053267 (6/16)*(5/16)*(5/11) Терять
7,7 0.140625 (6/16)*(6/16) Победить
6,7,7 0.092975 (5/16)*(6/11)*(6/11) Победить
8,7,7 0.092975 (5/16)*(6/11)*(6/11) Победить
7,6,7 0.06392 (6/16)*(5/16)*(6/11) Победить
7,8,7 0.06392 (6/16)*(5/16)*(6/11) Победить

В принципе, преимущество стороны с 6 и 8 заключается в том, что эти числа можно выбить в любом порядке: сначала 6, потом 8, или сначала 8, потом 6. С двумя семерками порядок выпадения только один: сначала 7, потом еще одна 7.

Два вопроса, пожалуйста: 1) Какова вероятность выпадения числа 6, 6, 6, 6, 6 за один раз на шестигранной игральной кости (6)? 2) Какова вероятность выпадения числа 1, 2, 3, 4, 5, 6 за один раз на шестигранной игральной кости (6)? Спасибо! Это меня просто убивает!

Heather от Petaluma

Вероятность выпадения шести шестерок составляет (1/6) 6 = 1 из 46656. Вероятность выпадения чисел 1, 2, 3, 4, 5, 6 на шести кубиках равна 6 ! /6 6 = 1 из 64,8
Какова вероятность того, что любое заданное число выпадет более одного раза при десятикратном броске игральной кости?

Ryan от Silay

1-(5/6) 10 -10 × (1/6) × (5/6) 9 = 51,55%.
В игре под названием «Налогообложение и уклонение от уплаты налогов» игрок бросает пару игральных костей. Если при любом броске сумма выпадает 7, 11 или 12, игрок подвергается налоговой проверке; при любой другой сумме он уклоняется от уплаты налогов. Если игрок бросает пару 5 раз, какова вероятность того, что он уклонится от уплаты налогов?

George P. от Stevens Point, WI

Вероятность выпадения 7, 11 или 12 равна (6+2+1)/36 = 9/36 = 1/4. См. мой раздел об основах вероятности при броске игральных костей , чтобы узнать, как я получил эту цифру. Вероятность выпадения чего-либо другого равна 3/4. Вероятность пяти бросков без выпадения 7, 11 или 12 равна (3/4) 5 = 23,73%.
Сколько бросков игральной кости нужно сделать, чтобы с высокой вероятностью хотя бы раз выпали числа 1, 2, 3, 4, 5 и 6? Есть ли идеи, как обобщить это для n-гранной игральной кости?

Asif от Columbia, SC

Не то чтобы вы спрашивали, но позвольте мне сначала рассмотреть среднее значение. Для шестигранной игральной кости ожидаемое количество бросков, при которых каждая грань выпадет хотя бы один раз, составляет (6/6)+(6/5)+(6/4)+(6/3)+(6/2)+(6/1) = 14,7. Для n-гранной игральной кости ожидаемое количество бросков составляет (n/n) + (n/(n-1)) + (n/(n-2)) + ... + n. Медианное количество необходимых бросков равно 13. Вероятность выпадения 13 или менее граней составляет 51,4%, а 13 или более граней — 56,21%.
Я знаю, вы скептически относитесь к контролю над броском кубиков. Я тренируюсь в расстановке кубиков и контролируемом броске уже 3 месяца. Какова вероятность выпадения 78 семерок из 655 случайных бросков? Спасибо за помощь :)

Eric B. от Boston, MA

Для большого количества бросков мы можем использовать аппроксимацию кривой Гаусса. Ожидаемое количество семерок из 655 бросков составляет 655 × (1/6) = 109,1667. Дисперсия равна 655 × (1/6) × (5/6) = 90,9722. Стандартное отклонение равно sqr(90,9722) = 9,5379. Ваши 78 семерок на 109,1667 − 78 = 31,1667 меньше ожидаемого значения. Это (31,1667 - 0,5)/9,5379 = 3,22 стандартных отклонения ниже ожидаемого значения. Вероятность отклонения на 3,22 или более стандартных отклонений от ожидаемого значения составляет 0,000641, или 1 к 1560. Этот результат я получил в Excel, используя формулу normsdist(-3.22).
Речь идёт о контроле над игральными костями в крэпсе. Ранее вы обсуждали Стэнфордский эксперимент Вонга , заявив: «Условием пари было то, смогут ли игроки, отличающиеся точностью бросков, выбросить менее 79,5 семёрок за 500 бросков костей. Ожидаемое число в случайной игре составило бы 83,33. Вероятность выпадения 79 или менее семёрок за 500 случайных бросков составляет 32,66%... Вероятность выпадения 74 или менее семёрок за 500 случайных бросков составляет 14,41%».

Вопрос, который у меня возникает по поводу этой ставки, заключается в том, что 14,41% все еще не является «статистически значимым» [т.е. p < 0,05], что обычно понимается как отклонение более чем на два стандартных отклонения от среднего значения — или вероятность того, что менее *совокупных* 5% событий произойдет случайным образом на любом из концов ряда.

Сколько семерок должно выпасть за 500 бросков, чтобы можно было сказать, что вероятность того, что результат был полностью случайным (то есть, статистически значимым), составляет менее 2,5%?

Большое спасибо! И кстати, ваш сайт — БЕЗУСЛОВНО ЛУЧШИЙ сайт по теме коэффициентов и вероятностей в азартных играх, который я нашел... Продолжайте в том же духе!!!

Plexus от Warwick, Rhode Island

Спасибо за добрые слова. Не следует говорить, что вероятность того, что броски были неслучайными, равна p. Правильнее было бы сформулировать это так: вероятность того, что случайная игра даст такой результат, равна p. Никто не ожидал, что 500 бросков что-либо докажут или опровергнут. Не я установил линию в 79,5 семерок, но сомневаюсь, что она была выбрана с целью статистической значимости; скорее, я подозреваю, что это была точка, при которой обе стороны согласились бы на пари.

Уровень значимости 2,5% составляет 1,96 стандартных отклонений от ожидаемого значения. Это можно рассчитать с помощью формулы =normsinv(0,025) в Excel. Стандартное отклонение для 500 бросков равно sqr(500*(1/6)*(5/6)) = 8,333. Таким образом, 1,96 стандартных отклонений — это 1,96 * 8,333 = 16,333 бросков в сторону меньше ожидаемого значения. Ожидаемое количество семерок в 500 бросках составляет 500*(1/6) = 83,333. Таким образом, 1,96 стандартных отклонений в сторону меньше этого значения равно 83,333 − 16,333 = 67. Проверив это с помощью биномиального распределения, получаем, что точная вероятность выпадения 67 или менее семерок составляет 2,627%.

Какое количество бросков кубиков потребуется, чтобы получить Ятзи?

Ian F. от Provo

Если предположить, что игрок всегда вытягивает наиболее часто встречающееся число, то среднее значение составляет 11,09. Ниже приведена таблица, показывающая распределение количества бросков в ходе случайной симуляции, включающей 82,6 миллиона испытаний.

Эксперимент «Яхтзи»

Роллы События Вероятность
1 63908 0.00077371
2 977954 0.0118396
3 2758635 0.0333975
4 4504806 0.0545376
5 5776444 0.0699327
6 6491538 0.0785901
7 6727992 0.0814527
8 6601612 0.0799227
9 6246388 0.0756221
10 5741778 0.0695131
11 5174553 0.0626459
12 4591986 0.0555931
13 4022755 0.0487016
14 3492745 0.042285
15 3008766 0.0364257
16 2577969 0.0312103
17 2193272 0.0265529
18 1864107 0.0225679
19 1575763 0.019077
20 1329971 0.0161013
21 1118788 0.0135446
22 940519 0.0113864
23 791107 0.00957757
24 661672 0.00801056
25 554937 0.00671837
26 463901 0.00561624
27 387339 0.00468933
28 324079 0.00392347
29 271321 0.00328476
30 225978 0.00273581
31 189012 0.00228828
32 157709 0.00190931
33 131845 0.00159619
34 109592 0.00132678
35 91327 0.00110565
36 76216 0.00092271
37 63433 0.00076795
38 52786 0.00063906
39 44122 0.00053417
40 36785 0.00044534
41 30834 0.00037329
42 25494 0.00030864
43 21170 0.0002563
44 17767 0.0002151
45 14657 0.00017745
46 12410 0.00015024
47 10299 0.00012469
48 8666 0.00010492
49 7355 0.00008904
50 5901 0.00007144
51 5017 0.00006074
52 4227 0.00005117
53 3452 0.00004179
54 2888 0.00003496
55 2470 0.0000299
56 2012 0.00002436
57 1626 0.00001969
58 1391 0.00001684
59 1135 0.00001374
60 924 0.00001119
61 840 0.00001017
62 694 0.0000084
63 534 0.00000646
64 498 0.00000603
65 372 0.0000045
66 316 0.00000383
67 286 0.00000346
68 224 0.00000271
69 197 0.00000238
70 160 0.00000194
71 125 0.00000151
72 86 0.00000104
73 79 0.00000096
74 94 0.00000114
75 70 0.00000085
76 64 0.00000077
77 38 0.00000046
78 42 0.00000051
79 27 0.00000033
80 33 0.0000004
81 16 0.00000019
82 18 0.00000022
83 19 0.00000023
84 14 0.00000017
85 6 0.00000007
86 4 0.00000005
87 9 0.00000011
88 4 0.00000005
89 5 0.00000006
90 5 0.00000006
91 1 0.00000001
92 6 0.00000007
93 1 0.00000001
94 3 0.00000004
95 1 0.00000001
96 1 0.00000001
97 2 0.00000002
102 1 0.00000001
Общий 82600000 1
Рассмотрим гипотетическую игру, основанную на броске игральной кости. Если выпадает 1, игрок проигрывает 1 доллар, и игра заканчивается. Если выпадает что-либо другое, игрок выигрывает 1 доллар. На этом этапе игрок может либо продолжить игру, либо выйти из неё. Игрок может продолжать играть, удваивая каждую ставку, пока не проиграет или не выйдет из игры. Какова наилучшая стратегия?

Byron P. от Newington, CT

Если говорить только о максимизации ожидаемой выгоды, игрок должен играть бесконечно. Хотя вероятность того, что игрок в конечном итоге проиграет, равна 1, в любой момент принятия решения ожидаемая выгода всегда склоняется в пользу повторной игры. Это кажется парадоксом. Ответ кроется в том, что некоторые события имеют вероятность 1, но всё же могут не произойти. Например, если вы бросили дротик в числовую прямую от 0 до 10, вероятность того, что он не попадёт точно в число пи, равна 1, но это всё ещё может произойти.

Однако на практике существует некий предел. Дело в том, что счастье, которое приносят деньги, не пропорционально их сумме. Хотя общепринято, что чем больше денег, тем больше счастья, чем богаче вы становитесь, тем меньше счастья приносит каждый дополнительный доллар.

Я считаю, что хороший способ ответить на этот вопрос — применить к задаче критерий Келли . Согласно Келли, игрок должен принимать каждое решение с целью максимизации ожидаемого логарифма своего банкролла после ставки. Если говорить коротко (я опустил много математических вычислений), игрок должен продолжать удваивать ставки до тех пор, пока сумма ставки не превысит 96,5948% от его общего состояния. Состояние определяется как сумма выигрыша плюс деньги, которые были у игрока до первой ставки. Например, если у игрока изначально было 100 000 долларов, он должен продолжать удваивать ставки до 23 раз, до выигрыша в 4 194 304 доллара. В этот момент общее состояние игрока составит 4 294 304 доллара. Ему будет предложено поставить 4 194 304 / 4 294 304 = 96,67% от его общего состояния, что превышает пороговое значение в 96,5948%, поэтому ему следует прекратить игру.

Игроки А и В бросают пару игральных костей. Игрок А выигрывает, если выпадет в сумме 6 раньше, чем В выпадет 7, а игрок В выигрывает, если выпадет 7 раньше, чем А выпадет 6. Если А начинает, покажите, что шансы А на победу составляют 30/61.

Sangeeta от Mumbai, India

Обозначим ответ на этот вопрос как p. Вероятность выпадения суммы шести кубиков равна 5/36, а вероятность выпадения суммы семи кубиков равна 6/36. Если вам непонятно почему, пожалуйста, ознакомьтесь с моим разделом об основах вероятности при броске кубиков . Мы можем определить p следующим образом:

p = Вероятность (6 при первом броске) + Вероятность (нет 6 при первом броске) * Вероятность (нет 7 при втором броске) * p.

Это происходит потому, что если ни один из игроков не выигрывает после первых двух бросков, игра возвращается в исходное состояние, и вероятность выигрыша игрока А остается неизменной.

Итак, у нас есть:

p = (5/36) + (31/36)×(30/36)×p
p = 5/36 + (930/1296)×p
п * (1-(930/1296)) = 5/36.
п * (366/1296) = 5/36
p = (5/36)×(1296/366) = 30/61.

Сколько существует способов бросить n шестигранных кубиков, результаты которых не различаются? Как уже говорилось, кубики не различаются, поэтому, например, при броске пяти кубиков, 1-1-3-5-6 и 1-6-5-1-3 будут считаться одним и тем же результатом. При броске двух кубиков легко определить, что ответ — 21, но я не могу найти элегантного, обобщенного решения.

Don от New York

Ответ можно выразить как combin(n+5,n) = (n+5)!/(120×n!). Вот ответ для игральных костей от 1 до 20.

Неразличимые комбинации кубиков

Кубики Комбинации
1 6
2 21
3 56
4 126
5 252
6 462
7 792
8 1287
9 2002
10 3003
11 4368
12 6188
13 8568
14 11628
15 15504
16 20349
17 26334
18 33649
19 42504
20 53130
21 65780
22 80730
23 98280

Благодарим Алана Такера, автора книги «Прикладная комбинаторика» .

Можно ли рассчитать вероятность того, что при броске игральных костей выпадут два числа одно за другим? То есть, какова вероятность того, что подряд выпадут две четверки, две шестерки или две семерки? Я понимаю, что прошлое не может предсказать будущее, но есть ли способ рассчитать вероятность того, что 7/36 x 7/36 выпадет подряд? Надеюсь, это понятно.

James от Birmingham

Конечно. Это будет Pr(2) ² + Pr(3) ² + ... + Pr(12) ² = (1/36) ² + (2/36) ² + (3/36) ² + (4/36) ² + (5/36) ² + (6/36) ² + (5/36) ² + (4/36) ² + (3/36) ² + (2/36) ² + (1/36) ² = 11,27%.
Сколько раз за 180 последовательных бросков игральных костей я могу ожидать увидеть следующее:

Две семерки подряд?
Три семерки подряд?
Четыре семерки подряд?

Спасибо за ваше время :-).

Melanie D. от Elizabeth City, NC

Я не вижу никакой полезной причины знать эту информацию, но меня часто об этом спрашивают, поэтому я вам отвечу.

Получить заданную последовательность семерок, начинающуюся с первого броска или заканчивающуюся последним, немного проще, потому что последовательность ограничена с одной стороны. В частности, вероятность получить последовательность из s семерок, начинающуюся с первого броска или заканчивающуюся последним, составляет (1/6) s × (5/6). Член 5/6 обусловлен тем, что в открытом конце последовательности должна выпасть не семерка.

Вероятность начала последовательности из s семерок в любой точке середины последовательности равна (1/6) s × (5/6) 2. Мы возводим член 5/6 в квадрат, потому что игрок должен получить не-7 на обоих концах последовательности.

Если выпало r бросков, то для внутренней последовательности будет 2 места, а для последовательности из n семерок — rn-1 место. Записав эти уравнения в таблицу, получаем ожидаемое количество последовательностей из семерок от 1 до 10. Столбец «внутри» равен 2*(5/6)*(1/6) r , а столбец «снаружи» — (179-r)*(5/6) 2 *(1/6) r , где r — количество семерок в последовательности. Таким образом, мы можем ожидать 3,46 последовательности из двух семерок, 0,57 последовательности из трех семерок и 0,10 последовательности из четырех семерок.

Ожидаемое количество выпадений семерок за 180 бросков

Бегать Внутри Снаружи Общий
1 0.277778 20.601852 20.87963
2 0.046296 3.414352 3.460648
3 0.007716 0.565844 0.57356
4 0.001286 0.093771 0.095057
5 0.000214 0.015539 0.015754
6 0.000036 0.002575 0.002611
7 0.000006 0.000427 0.000433
8 0.000001 0.000071 0.000072
9 0 0.000012 0.000012
10 0 0.000002 0.000002
Бросаются две игральные кости до тех пор, пока сумма не достигнет 12 или двух последовательных сумм, равных 7. Какова вероятность того, что первым выпадет 12?

анонимный

Ответ и решение можно найти на моем дополнительном сайте mathproblems.info , задача 201.
Я увлекаюсь настольными играми и обсуждал с друзьями некубические игральные кости из платоновых тел (если вы достаточно большой фанат, то это d4, d8, d12 и d20). Они утверждали, что только они были бы доказуемо честными. Я же возразил, что производство честных костей было бы слишком сложным. Кроме того, единственными играми, в которые можно было бы играть, были бы варианты крэпса, которые стали бы чрезмерно громоздкими из-за большого количества дополнительных исходов. Было ли когда-нибудь в казино игра с использованием нетрадиционных шестигранных костей?

Bayani от Carnagie, PA


Это Лиза Фурман, модель из моего обзора казино M. Когда я попытался произвести на неё впечатление, сказав, что фигурка из воздушного шара слева — это усечённый икосаэдр , она лишь улыбнулась и закатила глаза.

Не смейте оспаривать мои знания математики! Будучи второкурсником старшей школы, я построил не только все платоновы тела из картона и изоленты, но и все архимедовы тела .

Если ограничиться правильными многоугольниками и захотеть, чтобы каждая грань имела одинаковую вероятность, то вы будете ограничены платоновыми телами. Однако, если можно снять требование к правильным многоугольникам, то можно добавить и 13 каталонских тел .

Отвечая на ваш другой вопрос, нет, я никогда не видел в казино игры, в которой использовались бы какие-либо игральные кости, кроме кубиков. Примерно десять лет назад я видел демонстрацию игры на игровой выставке в Атлантик-Сити, в которой, как мне кажется, использовался ромбический триаконтаэдр , одно из каталонских тел, но, думаю, она так и не попала в казино. На выставке Global Gaming Expo я каждый год вижу игру с вращающимся волчком (похожим на дрейдл), но, увы, я никогда не видел её в казино.

Если я брошу три шестигранных кубика, какова вероятность выпадения стрита и, соответственно, какова вероятность выпадения тройки одинаковых чисел?

Mark от Fargo, ND

Существует 6³ = 216 способов бросить три игральные кости. Шесть из этих комбинаций приведут к выпадению трех одинаковых чисел (от 1-1-1 до 6-6-6). Таким образом, вероятность выпадения трех одинаковых чисел составляет 6/216 = 1/36. Существует четыре возможных варианта для стрита (от 1-2-3 до 4-5-6). Также существует 3! = 6 способов расположить три игральные кости в стрит. Таким образом, существует 4*6 = 24 комбинации для стрита. Следовательно, вероятность выпадения стрита составляет 24/216 = 1/9.
Какова средняя сумма, полученная при броске четырех шестигранных кубиков после вычитания наименьшего результата (обозначаемого как 4d6-L)? Каково стандартное отклонение для этого броска?

Aaron от New York

В следующей таблице показано количество комбинаций для всех возможных сумм от 3 до 18.

Комбинации в 4d6-L

Исход Комбинации
3 1
4 4
5 10
6 21
7 38
8 62
9 91
10 122
11 148
12 167
13 172
14 160
15 131
16 94
17 54
18 21
Общий 1296

Средний результат составляет 12,2446, а стандартное отклонение — 2,8468.

Мой вопрос основан на вероятности выпадения чисел на игральных костях. Я знаю, что есть шесть способов получить 7 и один способ получить 12, но каковы шансы получить шесть семерок до одной двенадцатки? Равны ли они, и если нет, то сколько двенадцаток нужно добавить к уравнению, чтобы вероятность стала равной?

nick

Вероятность выпадения 7 составляет 1/6, а вероятность выпадения 12 — 1/36. Вероятность выпадения 7 при условии, что выпало 7 или 12, равна (1/6)/((1/6)+(1/36)) = 6/7. Таким образом, вероятность того, что первые шесть раз, когда выпадает 6 или 12, это всегда будет 6, составляет (6/7) 6 = 39,66%.

Если переформулировать вопрос так: какова вероятность выпадения пяти шестерок до двенадцати? Тогда ответ будет (6/7) ·5 = 46,27%. При четырех бросках вероятность составит (6/7) ·4 = 53,98%. Таким образом, нет такого количества семерок до двенадцати, вероятность которого была бы ровно 50/50. Если вы ищете выгодную ставку, предложите либо четыре семерки до двенадцати, либо двенадцать до пяти семерок.

Этот вопрос был поднят и обсужден на форуме моего дочернего сайта Wizard of Vegas .

Существует ли простой способ рассчитать вероятность выпадения числа t при бросании d шестигранных игральных костей?

Anon E. Mouse

Вот полезный трюк от Роберта Гудханда из Сомерсета, Великобритания. Сначала поместите в ряд шесть единиц, окруженных пятью нулями с каждой стороны, следующим образом:

Вероятности выпадения одной игральной кости

Сумма выпавших кубиков 1 2 3 4 5 6
Одна игральная кость 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0

Это показывает количество комбинаций, при которых на одном кубике выпадает число от 1 до 6. Знаю, довольно очевидно. Но давайте разберемся. Для двух кубиков добавьте еще одну строку внизу, и для каждой ячейки возьмите сумму значений строки выше и пяти ячеек слева от нее. Затем добавьте еще пять фиктивных нулей справа, если хотите продолжить. Это показывает количество комбинаций, при которых выпадает сумма от 2 до 12.

Вероятности двух игральных костей

Сумма выпавших кубиков 2 3 4 5 6 7 8 9 10 11 12
Одна игральная кость 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0
Две игральные кости 0 0 0 0 0 1 2 3 4 5 6 5 4 3 2 1 0 0 0 0 0

Для трех кубиков просто повторите. Это будет представлять количество комбинаций от 3 до 18.

Вероятности трех игральных костей разлагаются в ряд.

Сумма выпавших кубиков 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
Одна игральная кость 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Две игральные кости 0 0 0 0 0 1 2 3 4 5 6 5 4 3 2 1 0 0 0 0 0 0 0 0 0 0
Три игральные кости 0 0 0 0 0 1 3 6 10 15 21 25 27 27 25 21 15 10 6 3 1 0 0 0 0 0

Чтобы вычислить вероятность любой заданной суммы, разделите количество комбинаций этой суммы на общее количество комбинаций. В случае с тремя игральными костями сумма равна 216, что также легко найти как 6³ . Например, вероятность выпадения суммы 13 при броске трех игральных костей составляет 21/216 = 9,72%.

Итак, для кубиков d вам нужно будет пройти путь от 1 до d-1. Это очень легко сделать в любой электронной таблице.

Сколько бросков двух игральных костей потребуется, чтобы иметь 50-процентную вероятность выпадения хотя бы одной цифры 12?

Maff

Это классическая задача в истории теории вероятностей. Многие ошибочно считают, что ответ — 18, потому что вероятность выпадения 12 составляет 1 к 36, а 18 × (1/36) = 50%. Однако, по этой логике, вероятность выпадения 12 из 36 бросков должна составлять 100%, что явно не так. Вот правильное решение. Пусть r — количество бросков. Вероятность того, что выпадет не 12, равна 35/36. Вероятность того, что из r бросков выпадет 0 12, равна (35/36) r . Таким образом, нам нужно найти r в следующем уравнении:

(35/36) r = 0,5
log(35/36) r = log(0.5)
r × log(35/36) = log(0.5)
r = log(0.5)/log(35/36)
r = 24,6051

Таким образом, округленного ответа нет. Вероятность выпадения 12 при 24 бросках составляет 1-(35/36) 24 = 49,14%. Вероятность выпадения 12 при 25 бросках составляет 1-(35/36) 25 = 50,55%.

Если вы хотите сделать ставку, допустим, вы сможете выбросить 12 за 25 бросков, или кто-то другой не сможет за 24 броска. В любом случае, у вас будет преимущество при равных шансах.

В игре Dice Wars , какова вероятность успеха при любом заданном количестве кубиков, используемых для атаки и защиты? Какое соотношение принесет атакующему наибольшую ожидаемую выгоду?

odiousgambit

Для тех, кто не знаком с игрой, поясним: и атакующий, и защищающийся бросают кубики от 1 до 8, в зависимости от количества армий, которыми они располагают на данном этапе сражения. Побеждает тот, у кого большее число. В случае ничьей побеждает защищающийся. Если атакующий проигрывает, он сохраняет одну армию на территории, где начал атаку. Поэтому для атаки ему необходимо иметь как минимум две армии, чтобы в случае победы одна армия могла занять захваченную территорию, а другая осталась на месте.

В следующей таблице показана вероятность победы нападающего при всех 64 комбинациях бросков кубиков.

Вероятность победы нападающего

Нападающий Защитник
1 армия 2 армии 3 армии 4 армии 5 армий 6 армий 7 армий 8 армий
2 0.837963 0.443673 0.152006 0.035880 0.006105 0.000766 0.000071 0.000005
3 0.972994 0.778549 0.453575 0.191701 0.060713 0.014879 0.002890 0.000452
4 0.997299 0.939236 0.742831 0.459528 0.220442 0.083423 0.025450 0.006379
5 0.999850 0.987940 0.909347 0.718078 0.463654 0.242449 0.103626 0.036742
6 0.999996 0.998217 0.975300 0.883953 0.699616 0.466731 0.259984 0.121507
7 1.000000 0.999801 0.994663 0.961536 0.862377 0.685165 0.469139 0.274376
8 1.000000 0.999983 0.999069 0.989534 0.947731 0.843874 0.673456 0.471091

В следующей таблице показана ожидаемая выгода для атакующего, определяемая как pr(количество побед атакующего)*(количество бросков кубиков защитника)+pr(количество побед защитника)*(количество бросков кубиков атакующего -1). Она показывает, что наибольшая ожидаемая выгода достигается при атаке с 8 очками против противника с 5 очками.

Чистая выгода от победы нападающего

Нападающий Защитник
1 армия 2 армии 3 армии 4 армии 5 армий 6 армий 7 армий 8 армий
2 0.675926 0.331019 -0.391976 -0.820600 -0.963370 -0.994638 -0.999432 -0.999955
3 0.918982 1.114196 0.267875 -0.849794 -1.575009 -1.880968 -1.973990 -1.995480
4 0.989196 1.696180 1.456986 0.216696 -1.236464 -2.249193 -2.745500 -2.929831
5 0.999250 1.927640 2.365429 1.744624 0.172886 -1.575510 -2.860114 -3.559096
6 0.999976 1.987519 2.802400 2.955577 1.996160 0.134041 -1.880192 -3.420409
7 1.000000 1.998408 2.951967 3.615360 3.486147 2.221980 0.098807 -2.158736
8 1.000000 1.999847 2.990690 3.884874 4.372772 3.970362 2.428384 0.066365

Какова вероятность составить комбинацию «Ятзи» при n бросках игральных костей?

анонимный

Для тех, кто не знаком с игрой, поясним: Ятзи — это комбинация из пяти одинаковых кубиков. В игре Ятзи игрок может оставить любые кубики, какие пожелает, и перебросить остальные. Он может сделать это до трех раз.

Игрок может перебросить ранее выпавшие кубики, если пожелает. Например, если при первом броске выпали 3-3-4-5-6, и у него остались тройки, а после второго броска — 3-3-5-5-5, он может оставить пятерки и перебросить тройки при третьем броске.

В следующей таблице показано максимальное количество одинаковых граней на кубиках за 1–20 бросков. Таблица показывает, что вероятность выпадения Ятзи в течение трех бросков составляет примерно 4,6%.

Вероятности в игре Яхтзи

Роллы Максимальное количество кубиков с одинаковой гранью.
Один Два Три Четыре Пять
1 0.092593 0.694444 0.192901 0.019290 0.000772
2 0.008573 0.450103 0.409022 0.119670 0.012631
3 0.000794 0.256011 0.452402 0.244765 0.046029
4 0.000074 0.142780 0.409140 0.347432 0.100575
5 0.000007 0.079373 0.337020 0.413093 0.170507
6 0.000001 0.044101 0.263441 0.443373 0.249085
7 0.000000 0.024501 0.199279 0.445718 0.330502
8 0.000000 0.013612 0.147462 0.428488 0.410438
9 0.000000 0.007562 0.107446 0.398981 0.486011
10 0.000000 0.004201 0.077416 0.362855 0.555528
11 0.000000 0.002334 0.055317 0.324175 0.618174
12 0.000000 0.001297 0.039279 0.285674 0.673750
13 0.000000 0.000720 0.027757 0.249063 0.722460
14 0.000000 0.000400 0.019543 0.215313 0.764744
15 0.000000 0.000222 0.013720 0.184883 0.801175
16 0.000000 0,000124 0.009610 0.157896 0.832371
17 0.000000 0.000069 0.006719 0.134258 0.858954
18 0.000000 0.000038 0.004692 0.113753 0.881517
19 0.000000 0.000021 0.003272 0.096100 0.900607
20 0.000000 0.000012 0.002280 0.080994 0.916714


Этот вопрос поднимается и обсуждается на моём форуме в Wizard of Vegas .
Мне интересно, что чаще выпадет при броске пары игральных костей — нечетное или четное число?

relaxmax

Ответ — 50/50. Это будет верно для любого количества брошенных кубиков, а не только для двух.

Немного не по теме, но я всегда считал, что комбинация четных и нечетных чисел была бы хорошей заменой ужасным крупным ставкам 6/8 в крэпсе. Чтобы дать казино преимущество, вот мои предлагаемые таблицы выплат и анализ.

Нечетная ставка

Событие Платит Комбинации Вероятность Возвращаться
3 или 11 1.5 4 0.111111 0.166667
5 или 9 1 8 0.222222 0.222222
7 0,5 6 0.166667 0.083333
Даже -1 18 0.500000 -0.500000
Общий 36 1.000000 -0.027778

Равная ставка

Событие Платит Комбинации Вероятность Возвращаться
2 или 12 3 2 0.055556 0.166667
4 или 10 1 6 0.166667 0.166667
6 или 8 0,5 10 0.277778 0.138889
Странный -1 18 0.500000 -0.500000
Общий 36 1.000000 -0.027778


Обращаем ваше внимание на то, что все права на данную публикацию принадлежат мне.

Этот вопрос поднимается и обсуждается на моём форуме в Wizard of Vegas .
В бонусной игре Hot Roll игрок выигрывает следующее количество монет в зависимости от суммы двух выпавших на кубиках чисел:

  • 2 или 12: 1000
  • 3 или 11: 600
  • 4 или 10: 400
  • 5 или 9: 300
  • 6 или 8: 200


Он продолжает бросать кубики, пока не выпадет в сумме семь, после чего бонусный раунд заканчивается. Если при первом броске выпадает семерка, он получает утешительный приз в размере 700 монет. Каково среднее количество монет, выигранных за один бонусный раунд?

анонимный

Среднее количество бросков обратно пропорционально вероятности события, завершающего бонусную игру, которая составляет 1/6, поэтому игрок в среднем совершит шесть бросков. Однако последний бросок будет седьмым, поэтому в среднем пять выигрышных бросков за бонусную игру.

Далее, вот вероятность каждого числа, если предположить, что семерка не выпадет:

  • 2 или 12: 1/30
  • 3 или 11: 2/30
  • 4 или 10: 3/30
  • 5 или 9: 4/30
  • 6 или 8: 5/30


Таким образом, средний выигрыш за один бросок, при условии отсутствия семерки, составляет 2*[(1/30)*1000 + (2/30)*600 + (3/30)*400 + (4/30)*300 + (5/30)*200] = 373,33.

Размер утешительного приза составляет (1/6)*700 = 116,67.

Таким образом, средний выигрыш по бонусам составляет 116,67 + 5 × 373,33 = 1983,33.

Какой был бы ответ на задачу с кубиками в рубрике «Спроси волшебника» № 179 , если бы игроки по очереди бросали кубики, и только игрок, бросивший кубик, мог бы продвинуться дальше в зависимости от результата броска?

анонимный

Вот первоначальный вопрос, заданный в столбце № 179: Если бросать две игральные кости снова и снова, пока не произойдет одно из следующих событий, то какое из них с большей вероятностью произойдет первым:

  • Выпадают числа шесть и восемь, в любом порядке, допускаются дубликаты.
  • Число семь выпадает дважды.

Суть в том, что один и тот же бросок кубика не может помочь обоим игрокам. Вместо этого они бросают кубики по очереди, и только тот, кто бросил, может использовать результат броска.

Ответ зависит от того, кто бросит кубик первым. Если первым бросает игрок, которому нужны шестерка и восьмерка, то вероятность его выигрыша составляет 57,487294%. Если первым ходит игрок, которому нужны две семерки, то вероятность выигрыша игрока, которому нужны шестерка и восьмерка, составляет 52,671614%. Я решил задачу, используя простой процесс цепи Маркова.

Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .

Предположим, у вас есть 12 шестигранных игральных костей. Вы бросаете их и можете отложить любые кости по своему желанию. Затем вы снова бросаете остальные кости. Какова вероятность выпадения 12 одинаковых чисел при двух бросках?

анонимный

При первом броске существует 58 различных типов последовательностей. Я определяю каждую по числу выпавших чисел, затем по общему числу выпавших чисел и так далее. Например, выпадение комбинации 3, 3, 3, 6, 6, 6, 5, 5, 2 будет обозначено как 4-3-2-1. В следующей таблице показано количество комбинаций каждой последовательности, вероятность её выпадения, вероятность выпадения 12 одинаковых чисел при втором броске и произведение этих двух значений. Для вероятности при втором броске я предполагаю, что игрок держит в руках кости с наибольшей суммой при первом броске. В нижней правой ячейке показана общая вероятность 0,0000037953, что равно 1 из 263 486.

12. Вопрос с игральными костями

Последовательность Комбинации Вероятность
Последовательность		 Условный
Вероятность		 Общий
Вероятность
12-0-0-0-0-0 6 0.0000000028 1.0000000000 0.0000000028
11-1-0-0-0-0 360 0.0000001654 0.1666666667 0.0000000276
10-2-0-0-0-0 1980 0.0000009096 0.0277777778 0.0000000253
10-1-1-0-0-0 7920 0.0000036384 0.0277777778 0.0000001011
9-3-0-0-0-0 6600 0.0000030320 0.0046296296 0.0000000140
9-2-1-0-0-0 79,200 0.0000363840 0.0046296296 0.0000001684
9-1-1-1-0-0 79,200 0.0000363840 0.0046296296 0.0000001684
8-4-0-0-0-0 14,850 0.0000068220 0.0007716049 0.0000000053
8-3-1-0-0-0 237,600 0.0001091519 0.0007716049 0.0000000842
8-2-2-0-0-0 178,200 0.0000818639 0.0007716049 0.0000000632
8-2-1-1-0-0 1 069 200 0.0004911837 0.0007716049 0.0000003790
8-1-1-1-1-0 356,400 0.0001637279 0.0007716049 0.0000001263
7-5-0-0-0-0 23,760 0.0000109152 0.0001286008 0.0000000014
7-4-1-0-0-0 475,200 0.0002183039 0.0001286008 0.0000000281
7-3-2-0-0-0 950,400 0.0004366077 0.0001286008 0.0000000561
7-3-1-1-0-0 2 851 200 0.0013098232 0.0001286008 0.0000001684
7-2-2-1-0-0 4 276 800 0.0019647348 0.0001286008 0.0000002527
7-2-1-1-1-0 5 702 400 0.0026196464 0.0001286008 0.0000003369
7-1-1-1-1-1 570,240 0.0002619646 0.0001286008 0.0000000337
6-6-0-0-0-0 13,860 0.0000063672 0.0000214335 0.0000000001
6-5-1-0-0-0 665,280 0.0003056254 0.0000214335 0.0000000066
6-4-2-0-0-0 1 663 200 0.0007640635 0.0000214335 0.0000000164
6-4-1-1-0-0 4 989 600 0.0022921906 0.0000214335 0.0000000491
6-3-3-0-0-0 1 108 800 0.0005093757 0.0000214335 0.0000000109
6-3-2-1-0-0 19 958 400 0.0091687624 0.0000214335 0.0000001965
6-3-1-1-1-0 13 305 600 0.0061125083 0.0000214335 0.0000001310
6-2-2-2-0-0 4 989 600 0.0022921906 0.0000214335 0.0000000491
6-2-2-1-1-0 29 937 600 0.0137531436 0.0000214335 0.0000002948
6-2-1-1-1-1 9 979 200 0.0045843812 0.0000214335 0.0000000983
5-5-2-0-0-0 997,920 0.0004584381 0.0000035722 0.0000000016
5-5-1-1-0-0 2 993 760 0.0013753144 0.0000035722 0.0000000049
5-4-3-0-0-0 3 326 400 0.0015281271 0.0000035722 0.0000000055
5-4-2-1-0-0 29 937 600 0.0137531436 0.0000035722 0.0000000491
5-4-1-1-1-0 19 958 400 0.0091687624 0.0000035722 0.0000000328
5-3-3-1-0-0 19 958 400 0.0091687624 0.0000035722 0.0000000328
5-3-2-2-0-0 29 937 600 0.0137531436 0.0000035722 0.0000000491
5-3-2-1-1-0 119,750,400 0.0550125743 0.0000035722 0.0000001965
5-3-1-1-1-1 19 958 400 0.0091687624 0.0000035722 0.0000000328
5-2-2-2-1- 59,875,200 0.0275062872 0.0000035722 0.0000000983
5-2-2-1-1-1 59,875,200 0.0275062872 0.0000035722 0.0000000983
4-4-4-0-0-0 693,000 0.0003183598 0.0000005954 0.0000000002
4-4-3-1-0-0 24 948 000 0.0114609530 0.0000005954 0.0000000068
4-4-2-2-0-0 18 711 000 0.0085957147 0.0000005954 0.0000000051
4-4-2-1-1-0 74 844 000 0.0343828589 0.0000005954 0.0000000205
4-4-1-1-1-1 12 474 000 0.0057304765 0.0000005954 0.0000000034
4-3-3-2-0-0 49 896 000 0.0229219060 0.0000005954 0.0000000136
4-3-3-1-1-0 99 792 000 0.0458438119 0.0000005954 0.0000000273
4-3-2-2-1-0 299 376 000 0.1375314358 0.0000005954 0.0000000819
4-3-2-1-1-1 199 584 000 0.0916876238 0.0000005954 0.0000000546
4-2-2-2-2-0 37 422 000 0.0171914295 0.0000005954 0.0000000102
4-2-2-2-1-1 149 688 000 0.0687657179 0.0000005954 0.0000000409
3-3-3-3-0-0 5 544 000 0.0025468784 0.0000000992 0.0000000003
3-3-3-2-1-0 133 056 000 0.0611250826 0.0000000992 0.0000000061
3-3-3-1-1-1 44 352 000 0.0203750275 0.0000000992 0.0000000020
3-3-2-2-2-0 99 792 000 0.0458438119 0.0000000992 0.0000000045
3-3-2-2-1-1 299 376 000 0.1375314358 0.0000000992 0.0000000136
3-2-2-2-2-1 149 688 000 0.0687657179 0.0000000992 0.0000000068
2-2-2-2-2-2 7 484 400 0.0034382859 0.0000000165 0.0000000001
Общий 2 176 782 336 1.0000000000 0.0000037953
В среднем, сколько бросков честной игральной кости необходимо, чтобы каждая грань выпала как минимум дважды?

Ace2

Нажмите на кнопку ниже, чтобы увидеть ответ.

Ответ: 1 172 906 043 / 48 600 000 = приблизительно 24,13387

Вот моё решение . (PDF)

Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .

Предположим, что бросают честную шестигранную игральную кость до тех пор, пока не выпадет 1, 2, 3 или 6. Если первым выпадает 1, 2 или 3 из этих чисел, определяющих исход игры, то вы ничего не выигрываете. Если первым выпадает 6 из этих чисел, определяющих исход игры, то вы выигрываете 1 доллар за каждый бросок кости. Каков средний выигрыш в этой игре?

Klopp

Нажмите на кнопку ниже, чтобы получить несколько формул бесконечных рядов, которые могут вам пригодиться.

Подсказка 1: Сумма чисел n от i = 0 до ∞ равна i = 1 / (1-n)

Подсказка 2: Сумма i × n для i от 0 до ∞ равна i = n / (1-n) ²

Нажмите на кнопку ниже, чтобы увидеть ответ.

Ответ - 3/4.

Нажмите на кнопку ниже, чтобы получить решение.

Предположим, что бросают честную шестигранную игральную кость до тех пор, пока не выпадет 1, 2, 3 или 6. Если первым выпадает 1, 2 или 3 из этих чисел, определяющих исход игры, то вы ничего не выигрываете. Если первым выпадает 6 из этих чисел, определяющих исход игры, то вы выигрываете 1 доллар за каждый бросок кости. Каков средний выигрыш в этой игре?

Подсказка 1: Сумма чисел n от i = 0 до ∞ равна i = 1 / (1-n)

Подсказка 2: Сумма i × n для i от 0 до ∞ равна i = n / (1-n) ²

Ожидаемый выигрыш можно выразить как сумму для i от 0 до ∞ (1 + i) * (1/3) i * (1/6). =

(1/6) * сумма для i от 0 до ∞ от (1/3) i + (1/6) * сумма для i от 0 до ∞ от (i * (1/3) i ).

Давайте рассмотрим их по очереди.

сумма для i от 0 до ∞ (1/3) i =

1 / (1 - (1/3)) =

1 / (2/3) =

3/2

Сумма для i от 0 до ∞ (i * (1/3) i ) =

(1/3) / (1 - (1/3)) 2 =

(1/3) / (4/9) =

(1/3) * (9/4) =

3/4

Если всё это сложить воедино, ответ таков:

(1/6) * (3/2) + (1/6)*(3/4) =

(1/4) + (1/8) =

3/8

Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .

Каково ожидаемое количество бросков честной игральной кости, при котором каждая грань выпадет не менее двух раз?

Ace2

Ответ: 390968681 / 16200000 = приблизительно 24.13386919753086

Хотя эту задачу можно было бы решить с помощью длинной и утомительной цепи Маркова, я предпочитаю интегральное решение. Я объясняю, как использовать этот метод, на своих страницах, посвященных игре Fire Bet и Bonus Craps .

Представьте, что вместо того, чтобы значимые события определялись броском игральной кости по одному, рассматривайте их как мгновение во времени. Предположим, что время между событиями обладает свойством отсутствия памяти, со средним временем между событиями в одну единицу времени. Другими словами, время между событиями подчиняется экспоненциальному распределению со средним значением 1. Это не будет иметь значения для целей разрешения пари, поскольку события по-прежнему происходят по одному.

Согласно распределению Пуассона, вероятность того, что любая заданная сторона игральной кости была брошена ноль раз за x единиц времени, равна exp(-x/6)*(x/6) 0 /0! = exp(-x/6). Также распределение Пуассона утверждает, что вероятность того, что любая заданная сторона была брошена ровно один раз, равна exp(-x/6)*(x/6) 1 /1! = exp(-x/6) * (x/6). Таким образом, вероятность того, что любая сторона была брошена два или более раз за x единиц времени, равна 1 - exp(-x/6)*(1 + (x/6)). Вероятность того, что все шесть сторон были брошены хотя бы дважды, равна (1 - exp(-x/6)*(1 + (x/6))) 6. Вероятность того, что хотя бы одна сторона не была брошена хотя бы дважды, равна:

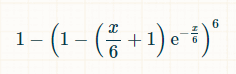
дважды прокатайте каждую сторону

Нам необходимо интегрировать эти данные по всему времени, чтобы определить, сколько времени в среднем пройдет, прежде чем желаемая цель будет достигнута.

К счастью, на этом этапе мы можем использовать калькулятор интегралов . Для калькулятора, ссылка на который приведена ниже, введите 1- (1 - exp(-x/6)*(1 + x/6))^6 dx = apx. 24.1338692 в текстовое поле после "Вычислить интеграл от" и в разделе "Пользовательский" установите границу интегрирования от 0 до ∞.

Ответ: 390968681 / 16200000 = приблизительно 24,13386919753086

Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .

Вы начинаете с честной шестигранной игральной кости и бросаете её шесть раз, записывая результаты каждого броска. Затем вы записываете эти числа на шесть граней другой, немаркированной честной игральной кости. Например, если ваши шесть бросков были 3, 5, 3, 6, 1 и 2, то на вашей второй кости не будет 4, а вместо этого будут две тройки.

Затем вы бросаете этот второй кубик шесть раз. Вы берете эти шесть чисел и записываете их на грани еще одного честного кубика, и продолжаете этот процесс создания нового кубика на основе предыдущего.

В конечном итоге у вас получится игральная кость с одинаковым числом на всех шести гранях. Каково среднее число переходов от одной кости к другой (или общее количество бросков, деленное на 6), необходимое для достижения этого состояния?

rsactuary

Прибл. 9.65599148388557

Давайте обозначим начальное состояние игральной кости буквами, а не цифрами, чтобы избежать путаницы. Давайте обозначим буквами каждое возможное состояние игральной кости. Например, AAABBC будет означать три одинаковых числа, два одинаковых числа и одно третье число. Начальное состояние, очевидно, будет ABCDEF.

Пусть E(ABCDEF) — ожидаемое количество бросков кубика из состояния ABCDEF.

E(ABCDEF) = 1 + [180 × E(AAAAAB) + 450 × E(AAAABB) + 300 × E(AAABBB) + 1800 × E(AAAABC) + 7200 × E(AAABBC) + 1800 × E(AABBCC) + 7200 × E(AAABCD) + 16200 × E(AABBCD) + 10800 × E(AABCDE) + 720 × E(ABCDEF)]/46656

Исходя из количества комбинаций перехода из одного состояния в другое, следующая матрица переходов показывает, сколькими способами можно перейти из каждого начального состояния (левый столбец) в каждое новое состояние. Кстати, на ее правильное построение ушло несколько часов.

Матрица переходов А

Состояние
До		 ААААААА АААААБ AAAABB AAABBB AAAABC AAABBC AABBCC AAABCD AABBCD AABCDE ABCDEF
АААААБ 15,626 18,780 9750 2500 - - - - - - -
AAAABB 4160 13,056 19 200 10,240 - - - - - - -
AAABBB 1458 8748 21,870 14,580 - - - - - - -
AAAABC 4098 12,348 8190 2580 7920 10,080 1440 - - - -
AAABBC 794 5172 8670 5020 6480 17,280 3240 - - - -
AABBCC 192 2304 5760 3840 5760 23,040 5760 - - - -
AAABCD 732 4464 4140 1680 7920 14 400 2520 4320 6480 - -
AABBCD 130 1,596 3150 1940 5,280 16,800 3600 4800 9360 - -
AABCDE 68 888 1380 760 3960 11,520 2520 7200 14,040 4320 -
ABCDEF 6 180 450 300 1,800 7200 1,800 7200 16 200 10,800 720

Я не буду вдаваться в долгие рассуждения по матричной алгебре, скажу лишь, что предположим, что матрица B имеет следующий вид:

Матрица B

Состояние
До		 АААААБ AAAABB AAABBB AAAABC AAABBC AABBCC AAABCD AABBCD AABCDE ABCDEF
АААААБ -27876 9750 2500 0 0 0 0 0 0 -46656
AAAABB 13056 -27456 10240 0 0 0 0 0 0 -46656
AAABBB 8748 21870 -32076 0 0 0 0 0 0 -46656
AAAABC 12348 8190 2580 -38736 10080 1440 0 0 0 -46656
AAABBC 5172 8670 5020 6480 -29376 3240 0 0 0 -46656
AABBCC 2304 5760 3840 5760 23040 -40896 0 0 0 -46656
AAABCD 4464 4140 1680 7920 14400 2520 -42336 6480 0 -46656
AABBCD 1596 3150 1940 5280 16800 3600 4800 -37296 0 -46656
AABCDE 888 1380 760 3960 11520 2520 7200 14040 -42336 -46656
ABCDEF 180 450 300 1800 7200 1800 7200 16200 10800 -46656

Ответом является отношение определителя матрицы B к определителю матрицы A:

Determ(A) = 1 461 067 501 120 670 000 000 000 000 000 000 000 000 000 000

Determ(B) = 14,108,055,348,203,100,000,000,000,000,000,000,000,000,000,000

Determ(B) / Determ(A) = приблизительно 9.65599148388557

Если вы бросаете одну игральную кость 20 раз, какова вероятность того, что хотя бы один раз выпадут все шесть граней?

Ace2

Приблизительный ответ: 0,847987541

[spoiler=Решение]

Ответ можно приблизительно выразить как 1 - (вероятность (нет единиц) + вероятность (нет двоек) + ... + вероятность (нет шестерок)) = 1 - 6*(5/6)^20 = приблизительно 0,84349568.

Однако это приведет к двойному вычитанию ситуаций, когда две разные стороны никогда не выпадали. Существует 15 комбинаций (6,2) = 15 способов выбрать две стороны из шести. Вероятность того, что любые две заданные стороны никогда не выпадут, составляет (4/6)^20. Нам нужно добавить эти значения к вероятности, потому что они были вычтены дважды на предыдущем шаге. Таким образом, теперь мы имеем 1 - 6*(5/6)^20 + 15*(4/6)^20 = приблизительно 0,84800661.

Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .

Однако, если какая-либо группа из трех сторон, которые никогда не выпадали, была бы вычтена трижды на первом шаге и сложена трижды на втором шаге, нам нужно вычесть их обратно, как если бы не все шесть сторон были выброшены. Существует комбинаций (6,3) = 20 способов выбрать три стороны из шести. Вероятность того, что какие-либо конкретные три стороны никогда не будут выброшены, составляет (3/6)^20. Таким образом, теперь мы имеем 1 - 6*(5/6)^20 + 15*(4/6)^20 - 20*(3/6)^20 = приблизительно 0,847987537.

Однако, если какая-либо группа из четырех сторон, которые никогда не выпадали, была бы вычтена вчетверо на первом шаге, добавлена вчетверо на втором шаге и вычтена вчетверо на третьем шаге, нам нужно добавить их обратно, потому что каждое такое состояние уже было вычтено дважды. Существует комбинаций (6,4) = 15 способов выбрать четыре стороны из шести. Вероятность того, что какие-либо конкретные четыре стороны никогда не будут выпадать, составляет (2/6)^20. Таким образом, теперь мы имеем 1 - 6*(5/6)^20 + 15*(4/6)^20 - 20*(3/6)^20 + 15*(2/6)^20 = приблизительно 0,84798754089.

Однако, если бы все 20 бросков были одинаковыми числами, то на первом шаге произошло бы пятикратное вычитание, на первом шаге — пятикратное добавление, на третьем шаге — пятикратное вычитание, и на четвертом шаге — пятикратное добавление. Нам нужно вычесть их обратно. Итак, теперь у нас есть 1 - 6*(5/6)^20 + 15*(4/6)^20 - 20*(3/6)^20 + 15*(2/6)^20 - 6*(1/6)^20 = приблизительно 0,84798754089.

Таким образом, ответ равен 1-6*(5/6)^20+COMBIN(6,4)*(4/6)^20-COMBIN(6,3)*(3/6)^20+COMBIN(6,2)*(2/6)^20-6*(1/6)^20 = приблизительно 0,84798754089.

У вас есть два кубика. Вы можете пронумеровать каждую сторону обоих кубиков по своему желанию, при условии, что каждая сторона является целым числом и больше или равна единице. Вы можете повторять одно и то же число на одном и том же кубике и доводить его до любого желаемого значения. Помимо создания стандартных кубиков, как можно пронумеровать их так, чтобы вероятность выпадения любой заданной суммы была такой же, как и при использовании стандартных кубиков?

анонимный

Кубик 1 = 1,2,2,3,3,4.
Кубик 2 = 1,3,4,5,6,8.

Боюсь, в этом случае мне пришлось действовать методом проб и ошибок.

Каково среднее количество бросков двух игральных костей, необходимых для получения всех сумм от 2 до 12?

анонимный

Ответ: 769767316159 / 12574325400 = приблизительно 61,2173847639572.

Для ответа на этот вопрос можно использовать цепь Маркова, но я предпочитаю дифференциальное исчисление. Ключевой момент заключается в том, что ответ будет тем же, если время между бросками распределено по экспоненциальному закону со средним значением, равным единице. При этом ответ можно выразить как интеграл от 0 до бесконечности от:

1-(1-exp(-x/36))^2*(1-exp(-x/18))^2*(1-exp(-x/12))^2*(1-exp(-x/9))^2*(1-exp(-5*x/36))^2*(1-exp(-x/6))

Вы легко можете решить такие интегралы с помощью калькулятора интегралов .

Вы также можете решить любую подобную задачу с помощью моего калькулятора ожидаемого количества испытаний .

Drop Dead — это игра, в которую играют пятью стандартными кубиками. Вы начинаете свой ход, бросая все пять кубиков. Если ни один из них не выпадает 2 или 5, вы суммируете броски, добавляете сумму к своему счету и бросаете снова. Если выпадают 2 или 5, ваш счет за бросок равен нулю. Все кубики, на которых выпали 2 или 5, объявляются «мертвыми» и откладываются в сторону. Затем вы бросаете снова оставшимися кубиками. Игра продолжается, и вы либо набираете очки, либо убираете кубики. Ваш ход заканчивается, когда все ваши кубики уничтожены, после чего говорят, что вы «умерли». Все ваши броски суммируются для получения вашего окончательного счета. Побеждает тот, у кого больше очков.

Какой результат вы ожидаете увидеть в этой игре?

Gialmere

16.064662

Начнём со сценария, когда осталась одна игральная кость, и будем двигаться в обратном направлении.

Пусть переменная a обозначает ожидаемое количество дополнительных очков при наличии одной оставшейся игральной кости.

Среднее значение броска кубика, не равное 2 или 5, составляет (1+3+4+6)/4 = 7/2.

a = (2/3)×(a + 7/2).

а/3 = 7/3.

а = 7.

Далее рассчитаем b, ожидаемое количество очков при наличии двух оставшихся игральных костей.

b = (2/3) 2 ×(b + 2 × (7/2)) + 2×(2/3)×(1/3)×a.

b = 11,2.

Далее рассчитаем c, ожидаемое количество очков при наличии трех оставшихся кубиков.

c = (2/3) 3 ×(c + 3× (7/2)) + 3×(2/3) 2 ×(1/3)×b + 3×(2/3)×(1/3) 2 ×b.

c = 1302/95 = 13,705263.

Далее рассчитаем d, ожидаемое количество точек при наличии четырех оставшихся игральных костей.

d = (2/3) 4 ×(d + 4× (7/2)) + 4×(2/3) 3 ×(1/3)×c + 6×(2/3) 2 ×(1/3) 2 ×b + 4×(2/3)×(1/3) 3 ×a.

d = 3752/247 = 15,190283.

Наконец, давайте рассчитаем e, ожидаемое количество очков при наличии пяти оставшихся игральных костей.

e = (2/3) 5 ×(e + 5×(7/2)) + 5×(2/3) 4 ×(1/3)×d + 10×(2/3) 3 ×(1/3) 2 ×c + 10×(2/3) 2 ×(1/3) 3 ×b + 5×(2/3)×(1/3) 4 ×a.

e = 16,064662.

Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .

Бросайте две игральные кости, красную и синюю, снова и снова. Записывайте сумму бросков каждой кости. Каково ожидаемое количество бросков, прежде чем суммарные значения этих двух костей сравняются?

teliot

Ответ — бесконечность.

Трудно объяснить, почему ответ равен бесконечности. Чтобы еще больше запутать и парадоксать ситуацию, вероятность того, что суммы когда-либо сравняются, равна 1.

В следующей таблице показана вероятность того, что итоговые суммы впервые совпадут после 1–16 бросков.

Вероятность равенства сумм впервые

Роллы Вероятность
1 0.166667
2 0.112654
3 0.092850
4 0.080944
5 0.072693
6 0.066539
7 0.061722
8 0.057819
9 0.054573
10 0.051819
11 0.049443
12 0.047367
13 0.045532
14 0.043895
15 0.042423
16 0.041089

В Excel очень точное соответствие этой кривой определяется формулой y = 0,1784*x-1,011, где x = количество бросков, а y = вероятность.

Сумма этого бесконечного ряда равна бесконечности.

Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .

Бросают пять красных и пять синих игральных костей. Какова вероятность того, что результаты броска обеих костей будут одинаковыми, независимо от порядка выпадения? Например, в обоих случаях выпадут 1-2-3-3-6.

анонимный

3557 / 559872 = 0,006353238, или примерно 1/157.

В таблице ниже представлены данные для любого типа рулонов:

  • Количество различных способов, которыми может быть получен этот результат. Например, для фулл-хауса существует шесть комбинаций для трех одинаковых карт и пять для пары, что в общей сложности составляет 30 различных фулл-хаусов.
  • Количество порядков. Например, для фулл-хауса существует combin(5,3)=10 способов выбрать три из пяти кубиков, чтобы получить три одинаковых числа. Два других кубика должны составлять пару.
  • Количество способов выпадения данной комбинации карт. Это произведение первых двух столбцов. Например, существует 30 * 10 = 300 способов выбросить фулл-хаус.
  • Вероятность выпадения комбинации. Например, для фулл-хауса вероятность составляет 300/6 5 = 0,038580.
  • Вероятность того, что оба броска выпадут одинаково и соответствуют данной комбинации карт. Это квадрат вероятности из четвертого столбца, деленный на квадрат вероятности из второго столбца. Например, вероятность того, что оба броска выпадут фулл-хаусом, составляет 0,038580² . Однако вероятность того, что они выпадут одинаковым фулл-хаусом, составляет 1/30. Таким образом, вероятность того, что оба броска выпадут одинаковым фулл-хаусом, равна 0,038580² /30 = 0,00004961.

В нижней правой ячейке показана общая вероятность того, что оба броска окажутся одинаковыми, равная 0,00635324.

Соответствующий рулон

Тип
рулона		 Другой
Типы		 Заказы Общий
Комбинации		 Вероятность
Один рулон		 Вероятность
Два рулона
Пять одинаковых 6 1 6 0.00077160 0.00000010
Четыре одинаковых 30 5 150 0.01929012 0.00001240
Аншлаг 30 10 300 0.03858025 0.00004961
Три одинаковых 60 20 1200 0.15432099 0.00039692
Две пары 60 30 1,800 0.23148148 0.00089306
Пара 60 60 3600 0.46296296 0.00357225
Пять отдельных особей 6 120 720 0.09259259 0.00142890
Общий 7776 1.00000000 0.00635324

Шестигранная игральная кость бросается до тех пор, пока не произойдет одно из следующих событий:

А) Любая из сторон появлялась шесть раз.
Б) Каждая сторона выступала как минимум один раз.

Какова вероятность того, что событие А произойдет первым?

Ace2

Чтобы ответить на этот вопрос, как я это сделал, используя методы дифференциального и интегрального исчисления, я рекомендую использовать калькулятор интегралов, например, тот, что находится на сайте integral-calculator.com/ .

Приблизительно 0,252635881662548

Вот моё решение (PDF).

Эта проблема (в несколько измененной формулировке) задается и обсуждается на моем форуме Wizard of Vegas .

Вы хотите сыграть в игру, для которой нужна обычная шестигранная игральная кость. К сожалению, вы проиграли кость. Однако у вас есть четыре карточки, которые вы можете пометить любым способом. Игрок должен выбрать две карточки случайным образом из четырех, без возвращения, и сложить значения этих двух карточек.

Как пронумеровать карты так, чтобы сумма чисел на двух разных картах соответствовала результату броска игральной кости?

Gialmere

Пронумеруйте их 0, 1, 2 и 4.

Существует шесть способов вытянуть две из четырех карт, а именно:

  • 0+1 = 1
  • 0+2 = 2
  • 1+2 = 3
  • 0+4 = 4
  • 1+4 = 5
  • 2+4 = 6

Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .

Шестигранная игральная кость бросается снова и снова до тех пор, пока сумма выпавших чисел не станет равной 13 или больше. Чему равны среднее арифметическое, медиана и мода итогового результата?

Gialmere

Среднее значение = 14,690219
Медиана = 14
Режим = 13

Для этого мне пришлось использовать цепь Маркова. В следующей таблице показана вероятность каждого итогового значения в зависимости от суммы, указанной в левом столбце. Начнем с очевидных случаев для сумм от 13 до 18. Затем, для сумм от 0 до 12, возьмем среднее значение шести ячеек ниже.

Вероятности для начального состояния, сумма которых равна 0, можно найти в первой строке.

Цепь Маркова

Сумма роллов 13 14 15 16 17 18
0 0.279263 0.236996 0.192313 0.145585 0.097371 0.048472
1 0.290830 0.230791 0.188524 0.143842 0.097114 0.048899
2 0.293393 0.241931 0.181893 0.139625 0.094943 0.048215
3 0.289288 0.245178 0.193717 0.133678 0.091410 0.046728
4 0.280369 0.242560 0.198450 0.146988 0.086950 0.044682
5 0.268094 0.235687 0.197878 0.153768 0.102306 0.042267
6 0.253604 0.225827 0.193419 0.155611 0.111500 0.060039
7 0.360232 0.193566 0.165788 0.133380 0.095572 0.051462
8 0.308771 0.308771 0.142104 0.114326 0.081919 0.044110
9 0.264660 0.264660 0.264660 0.097994 0.070216 0.037809
10 0.226852 0.226852 0.226852 0.226852 0.060185 0.032407
11 0.194444 0.194444 0.194444 0.194444 0.194444 0.027778
12 0.166667 0.166667 0.166667 0.166667 0.166667 0.166667
13 1.000000 0.000000 0.000000 0.000000 0.000000 0.000000
14 0.000000 1.000000 0.000000 0.000000 0.000000 0.000000
15 0.000000 0.000000 1.000000 0.000000 0.000000 0.000000
16 0.000000 0.000000 0.000000 1.000000 0.000000 0.000000
17 0.000000 0.000000 0.000000 0.000000 1.000000 0.000000
18 0.000000 0.000000 0.000000 0.000000 0.000000 1.000000

Этот вопрос задаётся и обсуждается на моём форуме " Волшебник из Вегаса" .

Как известно, ставка «Все» в крэпсе выигрывает, если все числа от 2 до 12, кроме 7, выпадают до того, как выпадет 7. Сколько в среднем бросков требуется, чтобы выиграть эту ставку, если она действительно выигрывает?

Ace2

20.989727251191...

Вот моё решение (PDF).

Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .

Я вижу, кто-то утверждает, что видел 18 последовательных выпадений «йо» (всего 11) за столом для игры в крэпс. Сколько в среднем бросков потребуется, чтобы это наблюдать?

Ace2

41 660 902 667 961 039 785 742 бросков.

Вот моё решение (PDF).

Две честные шестигранные игральные кости бросаются снова и снова до тех пор, пока не произойдет одно из следующих двух событий:

А) В общей сложности выпало 12.
B) Дважды подряд выпадает число 7.

Что, скорее всего, произойдёт первым?

анонимный

Всего 12.

[spoiler=Решение]

Позволять:

  • p = Вероятность того, что первым выпадет число 12 из исходного состояния или в любой момент, когда предыдущий бросок не выпал на 7.
  • q = Вероятность того, что при предыдущем броске выпадет 12, если 7 было 7.

Это называется задачей о цепи Маркова.

Прежде чем мы перейдем к этому, вспомним, что вероятность выпадения суммы 7 составляет 1/6, а 12 — 1/36.

Мы можем определить p и q через друг друга следующим образом:

  • (1) p = (1/36) + (6/36)q + (29/36)p
  • (2) q = (1/36) + (29/36)p

Умножим уравнение (1) на 36:

36p = 1 + 6q + 29p
(3) 7p = 1 + 6q

Подставим значение q из (2) в (3):

7п = 1 + 6*((1/36) + (29/36)п)
7p = 1 + (1/6) + (29/6)p
42p = 6 + 1 + 29p
13p = 7
q = 7/13

Таким образом, вероятность того, что первым выпадет 12, составляет 7/13 ≈ 53,85%.

Вероятность выпадения двух последовательных семерок составляет, таким образом, 46,15%.

Таким образом, более вероятно, что сначала выпадет число 12.