Телевизионные игровые шоу - Часто задаваемые вопросы
Это не совсем азартная игра, но меня всегда интересовало в телеигре «Цена правильная»: какая лучшая стратегия при вращении большого колеса, если вы не последний, кто вращает колесо? Предположим, вы не можете контролировать свой ход (результат полностью случаен), шаг в 5 центов от 0,05 до 1,00 доллара, вы получаете один или два вращения, сумма которых не превышает 1,00. При какой сумме не следует делать второй ход, чтобы иметь наилучшие шансы обыграть игрока, который вращает колесо после вас?
Если результат его первого вращения составил 65 центов или меньше, игрок, сделавший первый бросок, должен сделать его еще раз.
Если выполняется хотя бы одно из следующих условий, второй игрок должен сделать еще один бросок.
- Его результат меньше, чем результат первого игрока.
- Его выигрыш составляет 50 центов или меньше.
- Его результат составляет 65 центов или меньше, и он сравнялся с первым игроком.
Какова оптимальная стратегия для игры в Плинко в телеигре «Цена правильная»?
Слева направо призы расположены следующим образом: 100, 500, 1000, 0, 10000, 0, 1000, 500, 100. Для идеального анализа мне необходимо знать точное расположение фишек на доске, но, просто взглянув на доску (см. ссылку выше), я твердо убежден, что игрок должен бросить шайбу прямо над призом в 10 000 долларов. Хотя он ограничен двумя нулями, все остальные призы меркнут по сравнению с главным призом. Поэтому стратегия игрока должна заключаться в максимизации вероятности получения главного приза, бросая шайбу прямо над ним. Чтобы подтвердить или опровергнуть свою гипотезу, я провел поиск, и нашел множество ссылок, посвященных изучению этой игры. Эта ( www.amstat.org/publications/jse/v9n3/biesterfeld.html ) — одна из лучших, которая согласуется с моим выводом. В документе, в частности, указывается, что ожидаемая стоимость попадания шайбы в центр составляет 2557,91 доллара, с каждой стороны от центра — 2265,92 доллара, и эта стоимость снижается по мере удаления от центра.
В телеигре «Давайте заключим сделку» есть три двери. Для примера, предположим, что за двумя дверями скрывается коза, а за одной — новая машина. Ведущий, Монти Холл, выбирает двух участников, которые должны выбрать дверь. Каждый раз Монти первым открывает дверь, за которой оказывается коза. Допустим, на этот раз она принадлежала первому участнику. Хотя Монти никогда этого не делал, что если бы он предложил другому участнику поменяться дверями, выбрав другую, неоткрытую дверь? Должен ли он это сделать?
Да! Ключ к этой проблеме в том, что ведущий по определению должен открыть дверь с козой. Он знает, за какой дверью находится машина, поэтому независимо от того, какие двери выберут игроки, он всегда может сначала показать козу. Этот вопрос известен как «парадокс Монти Холла». Большая часть путаницы вокруг него возникает из-за того, что часто при формулировке вопроса ошибочно не уточняется, что ведущий знает, где находится машина, и всегда сначала показывает козу. Я думаю, часть вины лежит на Мэрилин Вос Савант , которая плохо сформулировала вопрос в своей колонке. Предположим, что приз находится за дверью № 1. Ниже описано, что произойдет, если у игрока (второго участника) будет стратегия не менять дверь.
- Игрок выбирает дверь №1 --> игрок побеждает
- Игрок выбирает дверь №2 --> игрок проигрывает
- Игрок выбирает дверь №3 --> игрок проигрывает
Ниже описано, что произойдет, если игрок выберет стратегию переключения.
- Игрок выбирает дверь 1 --> Ведущий показывает козу за дверью 2 или 3 --> игрок переключается на другую дверь --> игрок проигрывает
- Игрок выбирает дверь 2 --> Ведущий показывает козу за дверью 3 --> игрок переключается на дверь 1 --> игрок побеждает
- Игрок выбирает дверь 3 --> Ведущий показывает козу за дверью 2 --> игрок переключается на дверь 1 --> игрок побеждает
Таким образом, не меняя тактику, игрок имеет 1/3 шанс на победу. Меняя тактику, игрок имеет 2/3 шанса на победу. Следовательно, игроку определенно следует сменить тактику.
Для более подробного ознакомления с парадоксом Монти Холла я рекомендую статью в Википедии .
Мой вопрос касается задачи, известной как «парадокс двух конвертов». Вы участвуете в телеигре. Перед вами два конверта, в каждом из которых находится неизвестная сумма денег. Вам говорят, что в одном конверте вдвое больше денег, чем в другом. Теперь вас просят выбрать один конверт. Вы выбираете один. В нем 50 000 долларов. Теперь вам говорят, что вы можете оставить выбранный конверт себе или обменять его на другой. Стоит ли обменять? Зная заранее, что вы можете обменять, это не имеет значения, поскольку вы просто выберете тот конверт, который вам в итоге нужен. Но поскольку вы узнаете об обмене только после того, как выберете конверт, то первоначальный выбор и возможность обмена — это два независимых события, верно? При этом, когда вы решаете обменять конверт или нет, в другом конверте либо вдвое больше, либо вдвое меньше денег, чем в вашем текущем конверте. То есть в нем либо 100 000 долларов, либо 25 000 долларов. Поскольку вероятность любого из этих событий составляет 50%, ожидаемая стоимость другого конверта составляет 62 500 долларов. В общем случае, если обозначить x как сумму, которую вы изначально выбрали, то ожидаемая стоимость другого конверта составляет 1,25x. Следовательно, обмен всегда будет правильным. Это правильно? Спасибо.
Я хорошо знаком с этой проблемой. Я рассматриваю её на своём сайте с математическими задачами , задача номер 6. Там я рассматриваю общий случай, включая случай, когда первый конверт вообще не заглядывают внутрь. Однако, отвечая на ваш вопрос, мы не можем игнорировать место проведения игры. Вы сказали, что это «игровое шоу». В большинстве игровых шоу выигрыш в 50 000 долларов — это неплохой результат. Немногие участники шоу «Цена правильная» когда-либо достигают такой суммы. Я предполагаю, что менее 50% игроков в шоу «Кто хочет стать миллионером» достигают такой суммы. Между тем, выигрыши в 25 000 долларов не являются чем-то необычным в игровых шоу. Автомобили регулярно выигрываются в «Цена правильная», их стоимость составляет около 25 000 долларов. Выигрыш в 32 000 долларов — распространённая сумма в шоу «Кто хочет стать миллионером». Средний выигрыш в Jeopardy за шоу составляет примерно 25 000 долларов. Великий Кен Дженнингс в среднем выиграл всего 34 091 доллар за свои 74 победы. Итак, моя точка зрения такова: 50 000 долларов — это неплохой выигрыш для телеигры, а выигрыши в 100 000 долларов встречаются гораздо реже, чем в 25 000. Таким образом, как знаток телеигр, я считаю, что в другом конверте с большей вероятностью окажется 25 000 долларов, чем 100 000. Поэтому в вашем примере я считаю, что лучше оставить 50 000 долларов. Это также показывает, что никогда нельзя предполагать, что вероятность того, что в другом конверте окажется вдвое меньше или вдвое больше, составляет ровно 50/50. Как только вы видите сумму и учитываете контекст места проведения игры, вы можете принять разумное решение о смене участника, что отбрасывает аргумент о коэффициенте 1,25x.
Мой вопрос касается телеигры «Deal or No Deal», очень популярной в Австралии и которая скоро появится в Англии. Участнику показывают двадцать шесть пронумерованных портфелей, в каждом из которых спрятана определенная сумма денег, от 50 центов до 200 000 долларов, как показано ниже.
- 0,50 доллара
- 1 доллар
- 2 доллара
- 5 долларов
- 10 долларов
- 25 долларов
- 50 долларов
- 75 долларов
- 100 долларов
- 150 долларов
- 250 долларов
- 500 долларов
- 750 долларов
- 1000 долларов
- 1500 долларов
- 2000 долларов
- 3000 долларов
- 5000 долларов
- 7500 долларов США
- 10 000 долларов
- 15 000 долларов
- 30 000 долларов
- 50 000 долларов
- 75 000 долларов США
- 100 000 долларов США
- 200 000 долларов США
Участник выбирает один из чемоданов, который становится ЕГО чемоданом. Методом исключения, открывая остальные чемоданы, он пытается определить, сколько денег в его чемодане, или будет ли разумнее принять «банковское предложение». Банковские предложения основаны на арифметическом среднем оставшихся чемоданов, но не эквивалентны ему. Таким образом, если в основном остались чемоданы с высокой стоимостью, высока вероятность того, что чемодан участника ценный, и, следовательно, банковское предложение будет щедрым. И наоборот, если игроку не так повезло, и он открыл более ценные чемоданы, то банковское предложение будет низким. Какова была бы лучшая стратегия, если бы вы были участником этой игры? Нематематическая стратегия, основанная на интуиции, заключалась бы в том, чтобы игнорировать банковские предложения и продолжать открывать чемоданы до тех пор, пока не будет открыт и исключен чемодан на 200 000 долларов, или пока не будут открыты и исключены чемоданы на 100 000 и 75 000 долларов. В чём заключается математическая основа этой игры, Волшебник?
В США только что стартовало шоу «Deal or No Deal». Правила звучат так же, как и раньше, за исключением того, что наши призы достигают миллиона долларов, и вот как это выглядит.
- 0,01
- 1
- 5
- 10
- 25
- 50
- 75
- 100
- 200
- 300
- 400
- 500
- 750
- 1000
- 5000
- 10000
- 25000
- 50000
- 75000
- 100000
- 200000
- 300000
- 400000
- 500000
- 750000
- 1000000
Вот как протекает игра:
- Игрок выбирает для себя один кейс
- Игрок открывает шесть из оставшихся 25 кейсов.
- Банкир делает предложение.
- Если игрок откажется, он откроет еще пять из 19 оставшихся кейсов.
- Банкир делает предложение.
- Если игрок откажется, он откроет еще четыре из 14 оставшихся кейсов.
- Банкир делает предложение.
- Если игрок откажется, он откроет еще три из 10 оставшихся кейсов.
- Банкир делает предложение.
- Если игрок откажется, он откроет еще два из 7 оставшихся кейсов.
- Банкир делает предложение.
- Если игрок откажется, он откроет еще одно из оставшихся дел.
- Повторяйте шаги 11 и 12 до тех пор, пока игрок не примет предложение или пока у него не останется последний нераскрытый кейс.
На следующем графике показана ожидаемая стоимость ставки игрока и предложение банкира.
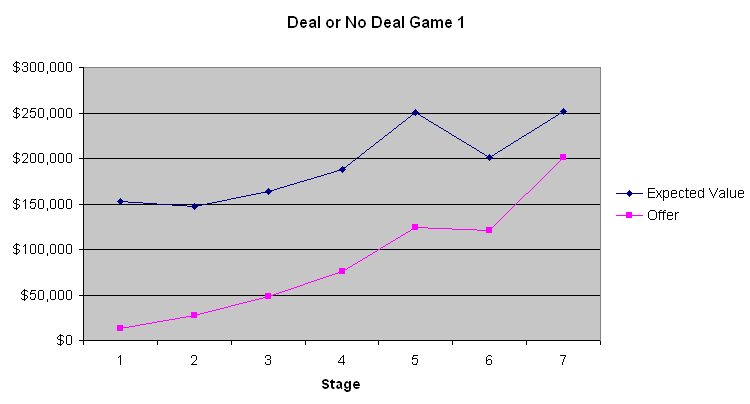
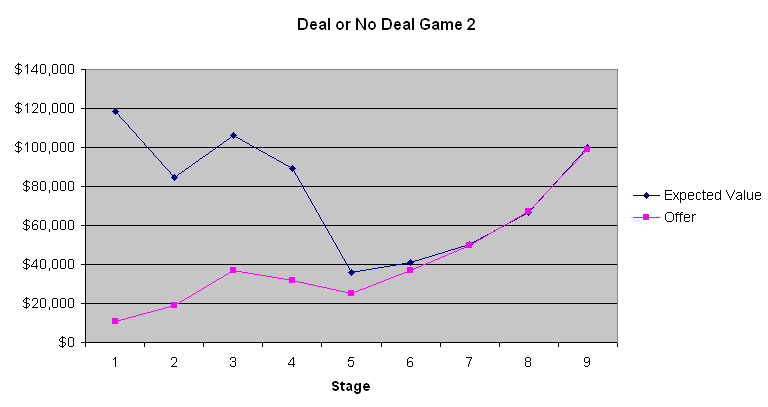
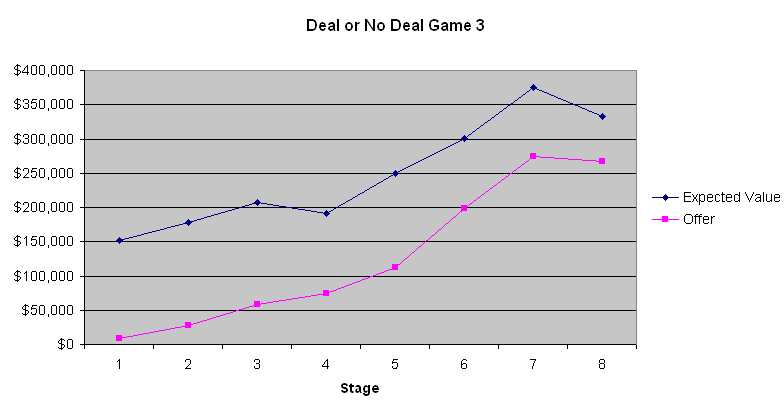
Самый очевидный вывод из этих трех диаграмм заключается в том, что первые четыре-шесть предложений от банка — это ужасные сделки. В среднем в чемодане находится 131 477,54 доллара до того, как его откроют. Предложить всего 9000–13000 долларов на первом этапе — это сделка, на которую пошел бы только дурак. Однако постепенно предложения становятся лучше. Вторая игра показывает, что ожидаемые значения были почти такими же, как предложения банкира к концу игры, когда ожидаемое значение для игрока было довольно низким. Однако в первой и третьей играх, когда ожидаемые значения были выше, банкир, по-видимому, пытался воспользоваться нежеланием большинства людей рисковать, когда речь идет о больших суммах. Не знаю, имело ли это значение, но участник во второй игре, похоже, был азартным игроком, который хотел выиграть по-крупному. Судя по комментариям ведущего, который общается с банкиром по телефону, банкир, похоже, принимает во внимание слова и действия участников. Если бы я был на месте банкира, я бы поступил примерно так же.
Если игрок не боится риска и не склонен к нему, а также игнорирует налоговые последствия, ему следует продолжать отказываться от предложений банкиров до тех пор, пока одно из них не превысит среднее значение оставшихся чемоданов. Для большинства людей прогрессивный характер подоходного налога благоприятствует заключению сделки. Как я уже говорил, я бы примерно сказал, что стоимость денег пропорциональна логарифму суммы. Поэтому, чем больше у вас денег в начале игры, тем больше у вас должно быть желания рисковать и отказываться от предложений банкиров. При таких больших суммах не существует стратегии, подходящей для всех. Однако я могу с достаточной уверенностью сказать, что игроку следует отказаться от первых четырех-шести предложений, а затем принимать решения в каждом конкретном случае (игра слов).
Ссылки:
Вы можете посмотреть шоу Deal or No Deal на сайте NBC.com.
Архив прошлых выступлений.
Смотрю "Сделку или нет". Понимаю, что "предложение" от банкира — это просто оставшаяся стоимость ящиков, деленная на их количество [с округлением]. Есть ли в этой игре хоть какая-то стратегия, или "сделка" всегда просто приемлема? Зависит ли это от количества открытых ящиков или чего-то подобного?
Как показывает моя статья от 26 декабря 2005 года, предложение банкира обычно значительно меньше, чем среднее значение в остальных случаях. Однако, гипотетически, если бы это всегда было так, то каждая стратегия имела бы одинаковую ожидаемую ценность. Игрок был бы безразличен к любому предложению.
В начале игры «Сделка или нет» вероятность выбрать кейс с выигрышем в 1 000 000 долларов составляет 1 к 26. После исключения всех кейсов, кроме одного, какова вероятность того, что мой кейс содержит миллион долларов? Это 50 на 50 или по-прежнему 1 к 26?
50-50
В вашей колонке от 5 апреля 2006 года вы утверждаете, что если в игре «Сделка или нет сделки» осталось всего два дела, и миллион долларов всё ещё разыгрывается, то вероятность того, что в моём деле окажется миллион, составляет 50 на 50. Я не согласен. Разве это не просто вариация задачи Монти Холла? То есть, миллион с большей вероятностью окажется на сцене, чем в его деле?
Нет. Многие со мной спорят по этому поводу. Многие авторы утверждают, что вероятности не могут измениться при добавлении дополнительной информации. Так, если вероятность начинается с 1 к 26, то она должна оставаться на этом уровне. Вопреки утверждениям продавцов систем ставок, вероятности действительно могут измениться при добавлении дополнительной информации. Я не хочу здесь объяснять основы теории вероятностей, но любой учебник по условной вероятности или теорема Байеса для колледжей должны хорошо осветить эту тему.
Позвольте мне объяснить, что произошло в программе «Давайте заключим сделку». Участник выбирал одну из трёх занавесок. За одной скрывался очень ценный приз, а за двумя другими — призы поменьше. Допустим, за одной занавеской находилась машина, а за двумя другими — коза. Тогда Монти всегда, повторяю, ВСЕГДА, открывал одну из двух невыбранных занавесок, чтобы показать козу. После сотен выпусков это означало бы, что Монти Холл (ведущий) знал, где находится машина, и намеренно открывал занавеску, за которой оказывалась коза. Очевидно, что когда игрок выбирал свою занавеску, вероятность того, что за ней находилась машина, составляла 1/3, а вероятность того, что за одной из двух невыбранных занавесок находилась машина, составляла 2/3. Таким образом, Монти предопределённо открыть невыбранную занавеску, содержащую цель. Предопределённость — ключевое слово здесь. Поскольку Монти не может открыть занавеску игрока на этом этапе, вероятность того, что за занавеской игрока окажется машина, остаётся на уровне 1/3. Вероятность того, что невыбранная занавеска покажет машину, остается на уровне 2/3, однако теперь вся вероятность сосредоточена на одной занавеске. Таким образом, после того, как коза будет показана, вероятность того, что машина окажется на занавеске игрока, составляет 1/3, а вероятность того, что машина окажется на другой неоткрытой занавеске, составляет 2/3, что делает переключение мудрым решением.
В следующей таблице показаны все возможные исходы. В случае, когда игрок выбрал занавеску с машиной, Монти произвольно открыл занавеску. Вы можете видеть, что если игрок не меняет выбор, вероятность выигрыша составляет 1/3, а если меняет — 2/3.
Давайте заключим сделку
| Игрок Выбирает | Машина | Занавес Открыто | Вероятность | Победа с помощью Переключение |
| 1 | 1 | 1 | 0% | н/д |
| 1 | 1 | 2 | 5,56% | Н |
| 1 | 1 | 3 | 5,56% | Н |
| 1 | 2 | 1 | 0% | н/д |
| 1 | 2 | 2 | 0% | н/д |
| 1 | 2 | 3 | 11,11% | Я |
| 1 | 3 | 1 | 0% | н/д |
| 1 | 3 | 2 | 11,11% | Я |
| 1 | 3 | 3 | 0% | н/д |
| 2 | 1 | 1 | 0% | н/д |
| 2 | 1 | 2 | 0% | н/д |
| 2 | 1 | 3 | 11,11% | Я |
| 2 | 2 | 1 | 5,56% | Н |
| 2 | 2 | 2 | 0% | н/д |
| 2 | 2 | 3 | 5,56% | Н |
| 2 | 3 | 1 | 11,11% | Я |
| 2 | 3 | 2 | 0% | н/д |
| 2 | 3 | 3 | 0% | н/д |
| 3 | 1 | 1 | 0% | н/д |
| 3 | 1 | 2 | 11,11% | Я |
| 3 | 1 | 3 | 0% | н/д |
| 3 | 2 | 1 | 11,11% | Я |
| 3 | 2 | 2 | 0% | н/д |
| 3 | 2 | 3 | 0% | н/д |
| 3 | 3 | 1 | 5,56% | Н |
| 3 | 3 | 2 | 5,56% | Н |
| 3 | 3 | 3 | 0% | н/д |
Между тем, в игре «Сделка или нет сделки» ничто не предопределено. Предположим, что в «Сделке или нет сделки» остались суммы в 0,01 доллара, 1 доллар и 1 000 000 долларов. При наличии трех оставшихся кейсов вполне возможно, что в открытом кейсе окажется миллион долларов. В следующей таблице показаны возможные исходы при наличии трех оставшихся кейсов. Помните, что игрок не может открыть свой собственный кейс.
Сделка или нет?
| Игрок Выбирает | миллион долларов | Случай Открыто | Вероятность | Победа с помощью Переключение |
| 1 | 1 | 1 | 0% | н/д |
| 1 | 1 | 2 | 5,56% | Н |
| 1 | 1 | 3 | 5,56% | Н |
| 1 | 2 | 1 | 0% | н/д |
| 1 | 2 | 2 | 5,56% | Безнадежно |
| 1 | 2 | 3 | 5,56% | Я |
| 1 | 3 | 1 | 0% | н/д |
| 1 | 3 | 2 | 5,56% | Я |
| 1 | 3 | 3 | 5,56% | Безнадежно |
| 2 | 1 | 1 | 5,56% | Безнадежно |
| 2 | 1 | 2 | 0% | н/д |
| 2 | 1 | 3 | 5,56% | Я |
| 2 | 2 | 1 | 5,56% | Н |
| 2 | 2 | 2 | 0% | н/д |
| 2 | 2 | 3 | 5,56% | Н |
| 2 | 3 | 1 | 5,56% | Я |
| 2 | 3 | 2 | 0% | н/д |
| 2 | 3 | 3 | 5,56% | Безнадежно |
| 3 | 1 | 1 | 5,56% | Безнадежно |
| 3 | 1 | 2 | 5,56% | Я |
| 3 | 1 | 3 | 0% | н/д |
| 3 | 2 | 1 | 5,56% | Я |
| 3 | 2 | 2 | 5,56% | Безнадежно |
| 3 | 2 | 3 | 0% | н/д |
| 3 | 3 | 1 | 5,56% | Н |
| 3 | 3 | 2 | 5,56% | Н |
| 3 | 3 | 3 | 0% | н/д |
В таблице «Сделка или нет» показано, что при наличии трех кейсов вероятность того, что игрок откроет кейс с миллионным призом, составляет 1/3 (выигрыш безнадежен), вероятность выигрыша игрока, сменившего кейс, составляет 1/3, а вероятность проигрыша игрока, сменившего кейс, также составляет 1/3. Таким образом, шансы на смену кейса одинаковы. Когда остается только два кейса, вероятность того, что в каждом из них будет более крупный приз, составляет 50/50.
Время для еще одного вопроса из «Сделки или нет». Допустим, после всех сделок с банкиром и выступлений Селин Дион у вас осталось два чемодана: на 500 000 долларов и на 1 000 000 долларов. Предложение банкира, я полагаю, будет чуть меньше 750 000 долларов. Какой бы вы выбрали? А если бы остались два чемодана на 0,01 доллара и на 1 000 000 долларов? Думаю, все дело в том, азартный вы человек или нет, и это никак не связано с вероятностями. Причина, по которой я спрашиваю, заключается в том, интересно, выиграет ли КТО-НИБУДЬ когда-нибудь 1 000 000 долларов (даже если он выбрал волшебный чемодан).
Когда призы становятся суммами, меняющими жизнь, мудрый игрок должен играть консервативно, стремясь к максимизации ожидаемой выгоды. Хорошая стратегия должна заключаться в максимизации ожидаемого счастья. Хорошей функцией для измерения счастья, на мой взгляд, является логарифм вашего общего богатства. Возьмем человека с уже имеющимся состоянием в 100 000 долларов, которому предлагаются два варианта: 0,01 доллара и 1 000 000 долларов. При выборе варианта «нет сделки» ожидаемое счастье составляет 0,5 * log(100 000,01 доллара) + 0,5 * log(1 100 000 долларов) = 5,520696. Пусть b — банковское предложение, в отношении которого игрок безразличен.
log(b) = 5,520696
b = 10 5.520696
b = 331 662,50 долл. США.
Таким образом, этот гипотетический игрок должен быть равнодушен к предложению банка в размере 331 662,50 долларов. Чем меньше у вас денег в начале игры, тем консервативнее вы должны играть. Обычно на поздних этапах игры предложения банка близки к ожидаемой сумме, иногда немного превышают её. Единственный рациональный случай, когда игрок может выиграть миллион, — это если у него было много денег в начале игры и/или предложения банка были необычайно скупыми. Похоже, продюсерам нравятся трудолюбивые люди из среднего класса, поэтому мы вряд ли увидим кого-то, кто может позволить себе быть легкомысленным, когда речь идёт о больших суммах. Я также никогда не видел, чтобы банк предлагал менее 90% от ожидаемой суммы на поздних этапах игры. Время, когда мы увидим, как кто-то выиграет миллион, — это когда на шоу появится заядлый игрок, который не может остановиться. Когда это произойдёт, я буду болеть за банкира.
Это продолжение обсуждения шоу «Сделка или нет», которое я недавно посмотрел впервые. Ваш анализ предполагает, что банк не знает стоимости денег в чемодане. Однако в шоу, которое я смотрел, в финале оба участника выбрали ценный чемодан, и обоим были предложены (или были бы предложены, поскольку один из них уже выбыл) сделки, превышающие ожидаемую стоимость (EV). В самом крайнем случае игроку «были бы» предложены 687 000 долларов, когда оставались две суммы в 500 000 и 750 000 долларов. Единственное рациональное объяснение этому — банкир знает стоимость чемодана игрока, и предлагаемые сделки основаны на этом.
Это всего лишь моё мнение, и отвечать не требуется.
Спасибо, что не ожидали ответа, но я обычно отвечаю на вопросы о телеиграх. В каждом эпизоде утверждается, что суммы в кейсах распределены случайным образом, и ни Хоуи, ни банкир не знают результатов. В программе «Давайте заключим сделку» этого никогда не утверждали, хотя Монти Холл, очевидно, знал. Я тоже видел, как банкир предлагал в качестве последнего предложения сумму, превышающую ожидаемую, особенно когда речь шла о крупных суммах. По моему твердому убеждению, это не потому, что банкир знает, что находится внутри кейса игрока. В 1950-х годах разразился огромный скандал, когда стало известно, что шоу «21» , как и другие, было подстроено. Нет никаких веских причин портить успешное шоу и целостность всех телеигр, чтобы присвоить часть призовых денег через предложения банкира.
Я могу предложить три теории, объясняющие, почему банкир иногда предлагает больше, чем в среднем по остальным случаям.
- В сериале пытаются изобразить банкира, который потеет от денег в своем кабинете. Хоуи Мандел часто комментирует настроение и тон голоса банкира. Возможно, это делает сериал более драматичным, представляя банкира как осторожного бухгалтера, предпочитающего минимизировать потери, чем рисковать выплатой крупного выигрыша.
- Настоящий банкир действительно избегает рисков. Это выходит за рамки моей компетенции, но, насколько я понимаю, игровые и реалити-шоу обычно производятся компаниями, независимыми от телеканала. Эти небольшие компании обращаются к страховой компании, чтобы снизить риск выигрыша участниками крупных призов. В таком случае страховая компания будет настоящим банкиром и может влиять на поведение банкира в шоу. Страховые компании, которые страхуют подобные нестандартные вещи, не являются гигантами и могут предпочитать действовать осторожно, когда речь идёт о больших суммах.
В вашем примере предложение банкира было на 9,92% выше ожидаемой стоимости. Если бы банкир следовал критерию Келли , такое предложение было бы сделано при общем капитале всего в 782 008 долларов, что меньше максимального приза. Ни одна уважающая себя страховая компания не стала бы быть настолько консервативной. Очевидно, что одной этой причины недостаточно, чтобы оправдать предложение в вашем примере.
- Шоу пытается выставить участников глупыми и жадными. Такие программы, как «Ты умнее пятиклассника?» и «Переход дороги в неположенном месте» из «Tonight Show», не имели бы успеха, если бы мы не получали удовольствие, смеясь над людьми, не разбирающимися в викторинах. Шоу «Друг или враг?» и «Самое слабое звено» превосходно разоблачали жадность в человеческой природе. Должен признаться, я испытываю чувство злорадства, когда участник отказывается от предложения, превышающего ожидаемую стоимость, и уходит с меньшей суммой в своем случае.
Я склонен думать, что причина кроется в сочетании этих трех факторов, но в основном в третьем.
Если бы я закончил этот ответ здесь, я уверен, что получил бы комментарии с вопросом, действительно ли были бы сделаны гипотетические предложения от банкиров. Подразумевается, что они преувеличены для драматического эффекта. Я зафиксировал подробности 13 игр. В одной из них, когда оставалось три кейса (1000 долларов; 5000 долларов; и 50 000 долларов), средняя сумма составила 18 667 долларов, а предложение — 21 000 долларов. Это на 12,5% выше ожидаемой стоимости. В другой игре, когда оставалось два кейса (400 долларов и 750 000 долларов), средняя сумма составила 375 200 долларов, а предложение — 400 000 долларов. Это на 6,6% выше ожидаемой стоимости. Поэтому я не вижу причин сомневаться в достоверности гипотетических предложений.
Ссылки:
Формула для игры «Сделка или нет» : На этой странице представлены старые и новые формулы для расчета банковского предложения, основанные на бесплатной игре на сайте «Сделка или нет».
Сколько бы вы поставили на место каждого из участников в финальном раунде викторины Jeopardy, имея такие результаты:
Игрок А: 10 000 долларов
Игрок Б: 8000 долларов
Игрок C: 3500 долларов
Позвольте мне начать с некоторых предположений. Во-первых, я буду исходить из того, что у трёх игроков нет предварительных знаний о правилах ставок в финальном раунде Jeopardy, за исключением вероятностей правильного ответа в представленной таблице. Во-вторых, я буду исходить из того, что знание категории ничем не поможет. В-третьих, я также буду исходить из того, что все три участника хотят победить, не желая брать с собой ещё одного игрока в случае ничьей.
Начнём с игрока C. Он должен предположить, что A может поставить 6001 доллар, чтобы остаться выше B, если B окажется прав. Однако, если A окажется неправ, его ставка снизится до 3999 долларов. В таком случае C нужно будет поставить как минимум 500 долларов и оказаться правым, чтобы обыграть A. Однако, на мой взгляд, если для победы необходимо быть правым, то лучше поставить по-крупному. Поэтому, если бы я был C, я бы поставил всё.
В разрывается между большой и маленькой ставкой. Небольшая ставка должна составлять 999 долларов или меньше, чтобы остаться выше С, если С окажется прав. Преимущество небольшой ставки в том, чтобы остаться выше С любой ценой, надеясь, что А поставит большую сумму и ошибется. Большая ставка не обязательно должна быть выигрышной, но она вполне может быть выигрышной. Преимущество большой ставки в том, чтобы надеяться, что А либо поставит маленькую сумму, либо поставит большую и ошибется, но в обоих случаях для этого необходимо, чтобы В оказался прав.
По сути, А хочет пойти тем же путем, что и В. Небольшая ставка для А может составлять от 0 до 1000 долларов, и эта сумма останется выше, чем у В, если В поставит 999 долларов. Крупная ставка должна составлять 6001 доллар, чтобы гарантировать выигрыш, если А окажется прав, и сохранить надежду, если В поставит большую сумму, а все три игрока окажутся неправы.
Чтобы оценить вероятность восьми возможных исходов правильных и неправильных ответов, я проанализировал результаты финального раунда Jeopardy за сезоны с 20 по 24 с сайта j-archive.com (сейчас недоступен). Вот как выглядят результаты, где игрок А лидирует, за ним следует игрок В, а С находится на последнем месте.
Возможные исходы в финальном раунде Jeopardy
| Игрок А | Игрок Б | Игрок С | Вероятность |
| Верно | Верно | Верно | 21,09% |
| Верно | Верно | Неправильный | 9,73% |
| Верно | Неправильный | Верно | 10,27% |
| Неправильный | Верно | Верно | 8,74% |
| Верно | Неправильный | Неправильный | 13,33% |
| Неправильный | Верно | Неправильный | 10,27% |
| Неправильный | Неправильный | Верно | 8,63% |
| Неправильный | Неправильный | Неправильный | 17,92% |
Используя логику теории игр, которую я объясняю в задаче 192 на своем сайте mathproblems.info , я обнаружил, что A и B должны рандомизировать свою стратегию следующим образом.
Игроку А следует делать крупные ставки с вероятностью 73,6% и мелкие — с вероятностью 26,4%.
Игроку B следует сделать крупную ставку с вероятностью 67,3% и небольшую — с вероятностью 32,7%.
Игроку C следует сделать крупную ставку с вероятностью 100,0%.
Если следовать этой стратегии, вероятность выигрыша каждого игрока будет следующей:
Игрок А: 66,48%
Игрок B: 27,27%
Игрок C: 6,25%
В качестве дополнения, исходя из приведенной выше таблицы, вероятность того, что лидер правильно ответит на финальный вопрос, составляет 54,4%, для игрока, занявшего второе место, — 49,8%, а для игрока, занявшего третье место, — 48,7%. Общая вероятность составляет 51,0%.
В качестве практического замечания, игроки действительно обладают знаниями о поведении игроков в ставках. На мой взгляд, игроки чаще делают крупные ставки, чем это математически оправдано. Интересно, что я считаю ставки в Daily Double слишком консервативными, чем это математически оправдано. Одна из причин, по которой, как мне кажется, Кен Дженнингс так хорошо себя показал, — это агрессивные ставки в Double Doubles. В любом случае, если бы я действительно участвовал в шоу, я бы предположил, что два других игрока делали бы агрессивные ставки. Таким образом, мои реальные ставки составили бы 6000 долларов за A (будучи вежливым с B), 0 долларов за B и 3495 долларов за C (оставляя небольшую сумму без ставки на случай, если A по глупости поставит все или все, кроме 1 доллара, и окажется неправ).
Прежде чем кто-нибудь начнет меня расспрашивать о том, как можно вытянуть случайное число в реальном месте проведения мероприятия, позвольте мне предложить стратегию Стэнфорда Вонга: использовать секундную стрелку часов, чтобы вытянуть случайное число от 1 до 60.
В Великобритании состоялась премьера нового игрового шоу под названием « Цвет денег ». Участнику случайным образом назначается целевая сумма, которая, как известно, варьируется от 55 000 до 79 000 фунтов стерлингов. Чтобы заработать деньги, он выбирает 10 из 20 банкоматов, каждый из которых содержит от 1000 до 20 000 фунтов стерлингов с шагом в 1000 фунтов. После выбора банкомата счетчик начинает отсчет с 1000 фунтов стерлингов с шагом в 1000 фунтов стерлингов.
Игрок может в любой момент крикнуть «Стоп!», и он получит на свой счёт сумму, отображаемую на экране. Если игрок не остановится вовремя, и в автомате закончатся деньги, он ничего не получит. Ведущая предоставляет статистику, такую как количество оставшихся автоматов, оставшаяся сумма выигрыша, средняя сумма, необходимая для выигрыша на одном автомате, и суммы, оставшиеся в автоматах.
Игрок может «играть на разрывах», то есть, если выбрана серия автоматов, например, на 4000, 5000 и 6000 фунтов стерлингов, то автомат гарантированно достигнет отметки в 7000 фунтов стерлингов, как только превысит 3000 фунтов стерлингов. Мой вопрос: какую стратегию должен использовать игрок?
Это как раз тот случай, когда я мог бы неделями заниматься анализом подобных вещей. К сожалению, я прочитал ваше сообщение почти через три месяца после того, как вы его написали, из-за большого количества нерешенных вопросов в рубрике «Спроси Волшебника». На странице Википедии , кажется, указано, что это шоу провалилось и было отменено. Тем не менее, это все равно представляет собой интересную проблему.
Хозяйка автомата любезно сообщает вам среднее количество очков, необходимое на каждом оставшемся автомате, чтобы добраться до своей игры. После нескольких часов раздумий я не могу придумать ничего лучше, чем установить целевое количество очков примерно на 25% выше требуемого среднего значения. Это всего лишь предположение, поэтому, пожалуйста, не просите меня доказывать, что это оптимально. Как вы отметили, также используйте промежутки между уже выбранными очками, никогда не останавливаясь непосредственно перед тем, как будет выбрано нужное количество очков.
Если осталось всего две машины, и общая сумма, необходимая для покупки, составляет 13 000 фунтов стерлингов или меньше, я бы постарался купить все в предпоследней машине. Если 14 000 фунтов стерлингов или больше, я бы постарался купить половину в следующей машине.
Если этот сериал возобновят, надеюсь, мои читатели из Великобритании мне об этом сообщат. Это тот тип головоломок, которыми я мог бы увлечься, как, например , головоломка «Вечность» , которая, по совпадению (или нет), тоже вышла за пределами Великобритании.
P.S. Почему в Великобритании слово "colour" пишется с окончанием "au"? Мне это непонятно.
Каков средний размер приза за один удар и оптимальная стратегия для игры «Ударь кучку» в программе «Цена правильная»?
Для тех, кто не знаком с правилами, они объяснены на сайте игры «Цена правильная» . Пожалуйста, уделите немного времени, чтобы перейти туда, если вы не знакомы с игрой, потому что я предполагаю, что вы знаете правила. Также есть несколько видеороликов игры на YouTube. Вот старый ролик , в котором показан второй шанс, но максимальный приз тогда составлял всего 10 000 долларов. Сейчас он составляет 25 000 долларов.
Для начала рассчитаем ожидаемую стоимость приза, который не предоставляется в рамках второго шанса. В следующей таблице показано, что среднее значение составляет 1371,74 доллара.
Вручение призов Punch a Bunch без второго шанса
| Приз | Число | Вероятность | Ожидаемая победа |
| 25000 | 1 | 0.021739 | 543.478261 |
| 10000 | 1 | 0.021739 | 217.391304 |
| 5000 | 3 | 0.065217 | 326.086957 |
| 1000 | 5 | 0.108696 | 108.695652 |
| 500 | 9 | 0.195652 | 97.826087 |
| 250 | 9 | 0.195652 | 48.913043 |
| 100 | 9 | 0.195652 | 19.565217 |
| 50 | 9 | 0.195652 | 9.782609 |
| Общий | 46 | 1.000000 | 1371.739130 |
Во-вторых, рассчитайте средний размер приза, который предоставляется обладателям второго шанса. В следующей таблице показано, что средний размер составляет 225 долларов.
Раздача призов Punch a Bunch в рамках программы Second Chance.
| Приз | Число | Вероятность | Ожидаемая победа |
| 500 | 1 | 0.250000 | 125.000000 |
| 250 | 1 | 0.250000 | 62.500000 |
| 100 | 1 | 0.250000 | 25.000000 |
| 50 | 1 | 0.250000 | 12.500000 |
| Общий | 4 | 1.000000 | 225.000000 |
В-третьих, создайте таблицу ожидаемой прибыли, основанную на количестве вторых шансов, которые получает игрок. Это можно сделать с помощью простых математических вычислений. Например, вероятность 2 вторых шансов составляет (4/50) × (3/49) × (46/48). Ожидаемый выигрыш при наличии s вторых шансов составляет 1371,74 долл. + s × 225 долл. В следующей таблице показана вероятность и средний выигрыш при наличии от 0 до 4 вторых шансов.
Стол возврата призов Punch a Bunch
| Второй шанс | Вероятность | Средний выигрыш | Ожидаемая победа |
| 4 | 0.000004 | 2271.739130 | 0.009864 |
| 3 | 0.000200 | 2046.739130 | 0.408815 |
| 2 | 0.004694 | 1821.739130 | 8.551020 |
| 1 | 0.075102 | 1596.739130 | 119.918367 |
| 0 | 0.920000 | 1371.739130 | 1262.000000 |
| Общий | 1.000000 | 1390.888067 |
Таким образом, средний выигрыш за один удар (включая дополнительные деньги за второй шанс) составляет 1390,89 долларов.
В следующей таблице представлена моя стратегия минимального выигрыша, который необходимо принять, в зависимости от количества оставшихся ударов. Обратите внимание, что игрок может достичь отметки в 1400 долларов, получив призы в размере 1000 + 250 + 100 + 50 долларов за три вторых шанса.
Стратегия "Ударь кучку"
| Осталось ударов | Минимальный уровень для стояния |
| 3 | 5000 долларов |
| 2 | 5000 долларов |
| 1 | 1400 долларов |
Этот вопрос был поднят и обсужден на форуме моего дочернего сайта Wizard of Vegas .
Какова была бы оптимальная стратегия распределения денег в телеигре «Million Dollar Money Drop», если бы вы не были уверены в ответе?
Для удобства других читателей позвольте мне сначала повторить правила.
- Команда игроков начинает с 1 000 000 долларов.
- Команде задают вопрос с несколькими вариантами ответа.
- Команда должна разделить его деньги между всеми возможными ответами. Деньги, поставленные на правильный ответ, позволят перейти к следующему вопросу.
- Команда должна полностью исключить как минимум один возможный ответ, не делая на него никаких ставок.
- Этот процесс повторяется в течение нескольких раундов. Игроку также предоставляется один шанс передумать.
Очевидно, если команда уверена в ответе, то он должен поставить все свои деньги на правильный ответ. Если же команда может сузить круг возможных ответов до двух, но присваивает каждому 50% вероятности быть правильным, то они должны разделить его деньги поровну между двумя вариантами.
Сложность возрастает, если команда склоняется к одному ответу, но не исключает полностью один или несколько других. Рассмотрим пример. Предположим, команда определяет вероятность каждого правильного ответа следующим образом: A 10%, B 20%, C 30%, D 40%. Как им следует разделить его деньги?
Я утверждаю, что ответ заключается в следовании критерию Келли . Вкратце, команда должна максимизировать логарифм своего состояния в каждом вопросе. Для этого необходимо учитывать, сколько богатства у вас уже есть.
Допустим, ваше текущее состояние, накопленное независимо от участия в шоу, составляет 100 000 долларов. Это ваш первый вопрос, поэтому у вас есть 1 000 000 долларов, полученных в рамках телеигры, которые нужно разделить. Сначала исключите вариант с наименьшей вероятностью, чтобы соответствовать правилам шоу. Затем вы хотите максимизировать 0,2 × log(100 000 + b * 1 000 000) + 0,3 × log(100 000 + c * 1 000 000) + 0,4 × log(100 000 + d * 1 000 000), где строчные буквы a, b и c обозначают долю, отведенную на каждый ответ.
Эту задачу можно решить с помощью дифференциального исчисления и решения трехчленного уравнения, методом проб и ошибок или, что мне больше нравится, функцией «поиск решения» в Excel. Какой бы метод вы ни использовали, правильный ответ — 18,9% на вариант B, 33,3% на вариант C и 47,8% на вариант D.
Конечно, никто из участников шоу не сможет выполнить все эти вычисления за отведенное время, не говоря уже о том, что за это время нужно еще и переместить много пачек наличных. Мой более практичный совет — просто разделить деньги пропорционально вашей оценке вероятности правильного ответа, предполагая, что наименее вероятный вариант невозможен. В примере это приведет к разделению 22,2% на вариант B, 33,3% на вариант C и 44,4% на вариант D.
Этот вопрос был поднят и обсужден на форуме моего дочернего сайта Wizard of Vegas .
В Мичиганской лотерее есть игра для трех игроков со следующими правилами: Есть ли какое-либо позиционное преимущество у игрока, ходящего последним в этой игре? Какова оптимальная стратегия для каждого игрока? Вот видеона YouTube, демонстрирующее игру.
Во-первых, ход последним не дает никакого преимущества в плане позиции. Поскольку игроки находятся в звукоизолированной кабине, пока играют предыдущие игроки, порядок не имеет значения.
Во-вторых, в игре должно существовать равновесие Нэша, при котором стратегия, направленная на то, чтобы остаться с результатом не менее x очков, будет превосходить любую другую стратегию. Вопрос в том, чтобы найти x.
Я задался вопросом: какой была бы стратегия, если бы вместо карты с номерами от 1 до 100 каждый игрок получал случайное число, равномерно распределенное между 0 и 1, и искал точку x, в которой идеальный логик был бы безразличен к тому, оставаться ли на месте или менять карту? Получив такой ответ, легко применить его к дискретному распределению от 1 до 100.
На этом я закончу говорить и позволю читателям самим разобраться в проблеме. Ответ и решение вы найдете по ссылкам ниже.
Ответ для непрерывного распределения от 0 до 1 .
Ответ для дискретного распределения от 1 до 100.
Моё решение вы найдёте здесь (PDF) .
Этот вопрос был поднят и обсуждался на моём форуме в Wizard of Vegas .
Предположим, что цены на товары неизвестны. Какова оптимальная стратегия для игры «Гонка» в телешоу «Цена правильная»?
Для тех, кто не знаком с правилами, поясним: игроку даются четыре ценника, и он должен разместить их на четырех предметах. Закончив, он дергает рычаг, который показывает количество правильных совпадений. Если у игрока меньше четырех правильных совпадений, он может переставить ценники и попробовать снова. Игрок может попробовать столько раз, сколько сможет, в течение 45 секунд.
Мой совет: всегда отправляйте вариант, который имеет шансы на победу, учитывая предыдущую историю выборов и результатов. Если первый результат равен 0, то не меняйте местами два набора из двух тегов, а вместо этого переместите все на одну позицию в любом направлении.
Если вам сложно разобраться в логике на ходу, я объясню это ниже. Чтобы использовать эту стратегию, присвойте различным тегам буквы A, B, C и D. Затем расположите их в указанном порядке слева направо на сцене. Всегда начинайте с ABCD. Затем найдите историю партитур ниже и выберите последовательность тегов, указанную для этой последовательности партитур.
Если 0, то BCDA
Если 0-0, то CDAB
Если 0-0-0, то DABC (обязательно победит)
Если 0-1, то BDAC
Если 0-1-0, то CADB (обязательно победит)
Если 0-1-1, то CDBA
Если 0-1-1-0, то DCAB (обязательно победит)
Если 0-2, то BADC
Если 0-2-0, то DCBA (обязательно победа)
Если 1, то ACDB
Если 1-0, то BDCA
Если 1-0-0, то CABD
Если 1-0-0-1, то CBAC (обязательно победит)
Если 1-1, то BDCA
Если 1-1-0, то CABD
Если 1-1-0-1, то CBAC (обязательно победит)
Если счет 1-1-1, то BCAD (обязательно победит)
Если 2, то ABDC
Если 2-0, то BACD (обязательно победит)
Если 2-1, то ACBD
Если 2-1-0, то DBCA
Если 2-1-1, то ADCB
Если 2-1-1-0, то CBAD (обязательно победит)
В следующей таблице показана вероятность каждого количества оборотов. В нижней правой ячейке указано ожидаемое количество оборотов 10/3.
Гоночная игра
| Повороты | Комбинации | Вероятность | Возвращаться |
|---|---|---|---|
| 1 | 1 | 0.041667 | 0.041667 |
| 2 | 4 | 0.166667 | 0.333333 |
| 3 | 8 | 0.333333 | 1.000000 |
| 4 | 8 | 0.333333 | 1.333333 |
| 5 | 3 | 0.125000 | 0.625000 |
| Общий | 24 | 1.000000 | 3.333333 |
Этот вопрос обсуждается на моём форуме Wizard of Vegas .
Какова вероятность того, что любой игрок выиграет 25 000 долларов в соревновании Showcase Showdown на шоу Price is Right?
Для пояснения другим читателям, позвольте мне объяснить, о чём вы говорите. «Showcase Showdown» — это игра, которая проводится в телешоу «The Price is Right». В «Showcase Showdown» каждый игрок по очереди вращает колесо, вероятность остановки которого на любой сумме, делящейся на 0,05 без остатка, от 0,05 до 1,00, одинакова. Если игроку не нравится результат первого вращения, он может вращать колесо ещё раз, добавляя результат второго вращения к результату первого. Однако, если результат превышает 1,00, игрок немедленно дисквалифицируется. В случае ничьей каждый игрок получает по одному вращению в дополнительном раунде, побеждает тот, кто выиграет по большему числу. В случае повторной ничьей процесс повторяется до тех пор, пока ничья не будет разрешена.
Главная цель Showcase Showdown — пройти в финал Showcase. Однако предусмотрены и денежные призы, которые можно получить сразу же:
- В первом раунде, если какой-либо игрок получит в общей сложности 1 доллар, будь то за один раз или за два вращения, он выиграет 1000 долларов.
- В первом и единственном первом раунде, определяющем победителя в случае ничьи, если колесо остановится на отметке $0,05 или $0,15, то игрок выигрывает $10 000.
- В первом и единственном первом раунде, определяющем победителя в случае ничьи, если колесо остановится на отметке $1,00, то игрок выигрывает $25 000.
В столбце № 101 я объясняю оптимальную стратегию для «Показательного противостояния». Предполагая, что эта стратегия будет соблюдена, следующая таблица ответит на ваши вопросы и многие другие.
Статистика показательных поединков
| Вопрос | Отвечать |
|---|---|
| Ожидается, что в первом раунде победители получат по 1000 долларов. | 0.253790 |
| Вероятность ничьей между двумя игроками | 0.113854 |
| Вероятность ничьей между тремя игроками | 0.004787 |
| Ожидается, что во втором раунде победители получат по 10 000 долларов. | 0.024207 |
| Ожидается, что во втором раунде победители получат по 25 000 долларов. | 0.012104 |
| Ожидаемая общая сумма призовых денег | 798,45 долларов США |
| Вероятность того, что любой конкретный игрок выиграет 1000 долларов. | 0.084597 |
| Вероятность того, что любой конкретный игрок выиграет 10 000 долларов. | 0.008069 |
| Вероятность того, что любой конкретный игрок выиграет 25 000 долларов. | 0.004035 |
В нижней строке таблицы показано, что если вы попадете в «Showcase Showdown», не учитывая порядок вращения барабанов, ваши шансы выиграть 25 000 долларов составляют 0,004035, или 1 к 248.
Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .
В телеигре «Survivor» было две команды: одна состояла из девяти игроков, другая — из шести. Затем их случайным образом разделили на три новые команды по пять человек в каждой. Каждая новая команда состояла из трёх членов прежней команды из девяти игроков и двух членов прежней команды из шести игроков. Какова вероятность такого распределения?
Назовем первую команду из девяти игроков командой 1, а команду из шести игроков — командой 2. Количество способов выбрать трех игроков из команды 1 и двух из команды 2 равно combin(9,3) × combin(6,2) = 1260. Общее количество способов выбрать пять из 15 игроков равно combin(15,5) = 3003. Таким образом, вероятность того, что первая команда разделится 3/2 в пользу команды 1, составляет 1260/3003 = 41,96%.
Если это произойдёт, то у команды 1 останется шесть игроков, а у команды 2 — четыре. Количество способов выбрать трёх игроков из команды 1 и двух из команды 2 равно combin(6,3)×combin(4,2) = 120. Общее количество способов выбрать пять из 10 оставшихся игроков равно combin(10,5) = 252. Таким образом, вероятность того, что вторая команда разделится поровну в пользу команды 1 (3/2), при условии, что первая команда уже разделилась таким образом (3/2), составляет 120/252 = 47,62%.
Если первые две новые команды разделятся поровну (3/2) в пользу бывшей команды №1, то последняя команда разделится поровну (3/2) между оставшимися командами.
Таким образом, ответ на ваш вопрос: 41,96% × 47,62% × 100% = 19,98%.
Формулы:
combin(x,y)=x!/((y!*(xy)!)
x! = 1*2*3*...*x
Этот вопрос поднимается и обсуждается на моём форуме в Wizard of Vegas .
Я думаю, что Джеймс Хольцхауэр намеренно проиграл Эмме в своей последней игре. Моё доказательство в том, что до этого он делал крупные ставки в каждой игре, а теперь вдруг стал ставить против Эммы совсем немного. Подозреваю, что продюсеры хотят, чтобы Кен Дженнингс вёл шоу после ухода Алекса. Шоу было бы более драматичным, если бы у ведущего были результаты обеих игр и выигранные деньги. Таким образом, они подкупили Джеймса, чтобы он сдал игру.
Позвольте мне обрисовать ситуацию. 3 июня 2019 года Джеймс был в шаге от того, чтобы побить рекорд по общей сумме выигрышей в обычных играх, который до сих пор составляет 2 520 700 долларов. Средний выигрыш Джеймса за игру был намного больше, чем ему было нужно для побития рекорда. Поэтому все взгляды 3 июня были прикованы к тому, чтобы увидеть, как будет побит рекорд.
Вместо этого Джеймс не только не побил рекорд, но и проиграл. Победительница, Эмма, продемонстрировала очень сильную стратегическую игру, а также хорошо справилась с нажатием кнопки и просто правильно ответила. Она играла так же, как обычно играл Джеймс. Перед финальным раундом счет был следующим:
- Эмма — 26 600 долларов
- Джеймс — 23 400 долларов
- Джей — 11 000 долларов
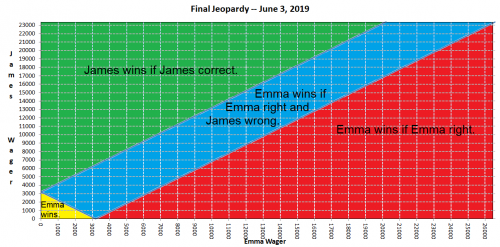
В ситуациях, когда у второго места больше половины очков первого, а у третьего — меньше, обычно всё сводится к тому, кто сделает ставку: на большую или маленькую. Большая ставка на первое место гарантирует победу, если результат окажется верным. Конкретнее, это удвоенный результат второго места минус результат первого места плюс один доллар. Именно так поступила Эмма, сделав ставку 2×$23 400 - $26 600 + $1 = $20 201. В большинстве случаев поступает именно так игрок, занявший первое место.
Однако Джеймс не знал, как Эмма решит, на что он сделает ставку. В следующей таблице показано, кто выиграет в зависимости от комбинации ставок.
Нажмите на изображение для увеличения.
Если Эмма сделает ставку не менее 20 201 доллара, то, в случае правильного ответа, она гарантированно выиграет.
Если Эмма делает низкую ставку, то она выиграет, если (а) Джеймс делает низкую ставку или (б) Джеймс делает высокую ставку и ошибается.
Если Джеймс делает высокую ставку, то он выигрывает, если (а) Эмма делает высокую ставку, Эмма ошибается, а Джеймс прав, или (б) Эмма делает низкую ставку, а Джеймс прав.
Если Джеймс делает низкую ставку, то он выигрывает, если же Эмма делает высокую ставку и ошибается.
Если бы играли идеальные логики, оба бы принимали решения случайным образом. Однако в ситуациях, когда его могут поймать, лидер редко выбирает низкий вариант. Если Джеймс предполагает, что Эмма выберет высокий вариант, то ему обязательно следует выбрать низкий. Таким образом, ему не нужно будет правильно ответить на финальный вопрос, чтобы выиграть, ему останется только надеяться, что Эмма проиграет.
Фактическая ставка Джеймса оказалась правильной суммой, чтобы покрыть ставку Джея, если бы тот поставил всё и оказался прав: 23 400 долларов - 2 × 11 000 долларов - 1 доллар = 1399 долларов, что считалось низкой ставкой для победы над Эммой.
Если это правда, Джеймс получит дополнительные 1000 долларов за второе место по сравнению с третьим.
В заключение, я категорически отвергаю теорию заговора о том, что Джеймс подстроил игру. Он играл правильно и проиграл из-за сочетания противостояния сильному сопернику и того, что большинство людей назвали бы «невезением».
Внешние ссылки
- Зал славы Jeopardy
- Джеймс Хольцхауэр о Jeopardy — обсуждение на моём форуме в Wizard of Vegas.
В финальном раунде викторины Jeopardy, какова оптимальная стратегия, если у игрока, занявшего второе место, более 2/3 денег, чем у игрока, занявшего первое место? Предположим, что игрок, занявший третье место, не является фактором.
Прежде всего, позвольте мне сделать оговорку. Приведенный ниже анализ основан на статистических средних значениях. Реальному игроку следует мысленно скорректировать свои знания категории «Финальный вопрос викторины», а также оценить шансы соперника дать правильный ответ.
Чтобы ответить на ваш вопрос, я сначала проанализировал данные четырех сезонов из архива Jeopardy, чтобы увидеть четыре возможные комбинации правильных и неправильных ответов игрока, занимающего первое (лидирующее) и второе (догоняющее) место в финальном раунде Jeopardy.
Итоговая таблица результатов викторины Jeopardy
| Ведущий игрок | Игрок, преследующий противника, прав. | Игрок, преследующий противника, неверен. | Общий |
|---|---|---|---|
| Правильный | 29,0% | 25,5% | 54,5% |
| Неверно | 17,7% | 27,8% | 45,5% |
| Общий | 46,8% | 53,2% | 100.0% |
Прежде чем продолжить, давайте определим некоторые переменные:
x = Вероятность того, что ведущий игрок выберет высокий результат.
y = Вероятность того, что преследующий игрок забьет высокий гол.
f(x,y) = Вероятность выигрыша игрока с более высоким рейтингом.
Выразим функцию f(x,y) через x и y из приведенной выше таблицы:
f(x,y) = 0.823xy + 0.545x(1-y) + 0.468(1-x)y + (1-x)(1-y)
f(x,y) = 0.810 xy - 0.455x - 0.532y + 1
Чтобы найти оптимальные значения для x и y, возьмём производную функции f(x,y) по обоим параметрам x и y.
f(x,y) d/dx = -0.455 + 0.810y = 0
Таким образом, y = 0,455/0,810 = 0,562
f(x,y) d/dy = -0.532 + 0.810x = 0
Таким образом, x = 0,523/0,810 = 0,657
Таким образом, игроку с высокими ставками следует делать высокие ставки с вероятностью 65,7%, а игроку с низкими ставками — высокие ставки с вероятностью 56,2%.
Судя по наблюдениям, я думаю, что игрок, делающий крупные ставки, делает их более чем в 65,7% случаев, поэтому, если бы я был на втором месте, я бы поставил более низкую ставку.
Если оба игрока следуют этой стратегии случайного выбора, вероятность победы лидирующего игрока составляет 70,1%.
Отбросив всю теорию, если вы лидируете, предскажите действия догоняющего игрока и поступите так же. Если вы догоняете, предскажите действия лидирующего игрока и поступите наоборот. Эта стратегия применима ко всем подобным турнирам.Этот вопрос поднимается и обсуждается на моём форуме в Wizard of Vegas .
Почему некоторые игроки, например Джеймс Хольцхауэр, в начале раунда «Jeopardy» начинают выбирать вопросы снизу? Разве не было бы логичнее начинать с более простых вопросов в начале раунда, отчасти для того, чтобы обеспечить правильное понимание категории, которая иногда бывает непростой?
Причина в том, что «Двойные выигрыши» в 91,5% случаев располагаются в нижних трех рядах. В следующей таблице показано их расположение на игровом поле для более чем 13 660 найденных «Двойных выигрышей».
Двойное количество мест
| Ряд | Столбец 1 | Столбец 2 | Столбец 3 | Столбец 4 | Столбец 5 | Столбец 6 | |
|---|---|---|---|---|---|---|---|
| 1 | 5 | - | 3 | 3 | 2 | 3 | 16 |
| 2 | 280 | 137 | 216 | 167 | 207 | 140 | 1,147 |
| 3 | 820 | 442 | 677 | 658 | 643 | 472 | 3712 |
| 4 | 1095 | 659 | 982 | 907 | 895 | 627 | 5165 |
| 5 | 787 | 403 | 670 | 671 | 613 | 476 | 3620 |
| Общий | 2987 | 1641 | 2548 | 2406 | 2360 | 1718 | 13,660 |
Источник: J! Archive .
Вот те же данные в виде частоты появления «Двойного выигрыша» в каждой ячейке игрового поля.
Вероятность двойного выигрыша в день
| Ряд | Столбец 1 | Столбец 2 | Столбец 3 | Столбец 4 | Столбец 5 | Столбец 6 | |
|---|---|---|---|---|---|---|---|
| 1 | 0,0% | 0,0% | 0,0% | 0,0% | 0,0% | 0,0% | 0,1% |
| 2 | 2,0% | 1,0% | 1,6% | 1,2% | 1,5% | 1,0% | 8,4% |
| 3 | 6,0% | 3,2% | 5,0% | 4,8% | 4,7% | 3,5% | 27,2% |
| 4 | 8,0% | 4,8% | 7,2% | 6,6% | 6,6% | 4,6% | 37,8% |
| 5 | 5,8% | 3,0% | 4,9% | 4,9% | 4,5% | 3,5% | 26,5% |
| Общий | 21,9% | 12,0% | 18,7% | 17,6% | 17,3% | 12,6% | 100.0% |
Причина поиска «Двойных выигрышей» заключается в том, что это хороший способ удвоить свой счет. У большинства участников вероятность правильного ответа на любой вопрос составляет от 80% до 90%. Это отличная возможность получить равные шансы на выигрыш, если у вас 80-90% шансов на победу. Одна из главных причин, по которой Джеймс Хольцхауэр выиграл так много раз, заключалась в агрессивном поиске «Двойных выигрышей» и, как правило, в ставках «все», когда они попадались. Именно так он проиграл Эмме, когда она применила ту же стратегию против него.
Какова наилучшая стратегия для игры в «Гонку» на телешоу «Цена правильная», если игрок не знает цен на призы?
Для тех читателей, кто не знаком с игрой, предлагаем посмотреть видеоролик.
Я утверждаю, что следующая стратегия обеспечивает минимальное среднее количество ходов. Существует множество стратегий, которые могли бы с ней сравниться, но я не думаю, что какая-либо из них сможет её превзойти.
Чтобы использовать эту стратегию, пронумеруйте четыре ценника как 1, 2, 3 и 4. Разместите их на четырех призах в соответствии с тем, сколько раз вы правильно ответили в прошлом, начиная с первого поворота слева.
Стратегия гоночной игры
| История | Приз 1 | Приз 2 | Приз 3 | Приз 4 |
|---|---|---|---|---|
| Никто | 1 | 2 | 3 | 4 |
| 0 | 2 | 1 | 4 | 3 |
| 0,0 | 3 | 4 | 2 | 1 |
| 0,0,0 | 4 | 3 | 1 | 2 |
| 0,0,2 | 3 | 4 | 1 | 2 |
| 0,0,2,0 | 4 | 3 | 2 | 1 |
| 0,2 | 2 | 3 | 4 | 1 |
| 0,2,0 | 4 | 1 | 2 | 3 |
| 0,2,1 | 2 | 4 | 1 | 3 |
| 0,2,1,0 | 3 | 1 | 4 | 2 |
| 1 | 1 | 3 | 4 | 2 |
| 1,0 | 2 | 4 | 3 | 1 |
| 1,0,0 | 3 | 1 | 2 | 4 |
| 1,0,0,0 | 4 | 2 | 1 | 3 |
| 1,1 | 1 | 4 | 2 | 3 |
| 1,1,0 | 2 | 3 | 1 | 4 |
| 1,1,0,0 | 3 | 2 | 4 | 1 |
| 1,1,0,0,0 | 4 | 1 | 3 | 2 |
| 2 | 2 | 1 | 3 | 4 |
| 2,0 | 1 | 2 | 4 | 3 |
| 2,1 | 1 | 3 | 2 | 4 |
| 2,1,0 | 4 | 2 | 3 | 1 |
| 2,1,1 | 1 | 4 | 3 | 2 |
| 2,1,1,0 | 3 | 2 | 1 | 4 |
В следующей таблице показана вероятность того, что потребуется от 1 до 5 оборотов из 24 возможных способов расположить четыре ценника.
Необходимое количество поворотов
| Повороты | Число | Вероятность |
|---|---|---|
| 1 | 1 | 4,17% |
| 2 | 4 | 16,67% |
| 3 | 8 | 33,33% |
| 4 | 9 | 37,50% |
| 5 | 2 | 8,33% |
| Общий | 24 | 100.00% |
Взяв скалярное произведение, получаем, что среднее количество оборотов, необходимых при этой стратегии, составляет 3,29167.
Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .
Я слышал о правиле двух третей при размещении ставок в финальном раунде викторины. Вы знаете об этом?
Да. Это означает изменение стратегии для второго игрока, если у него более 2/3 очков, чем у игрока, занявшего первое место.
Давайте упростим ситуацию до игры для двух игроков, следующим образом:
- Ситуация А: У команды, занявшей второе место, меньше половины очков, чем у команды, занявшей первое место.
- Ситуация B: Второй игрок занимает от 1/2 до 2/3 первого места.
- Ситуация C: Второе место занимает более 2/3 участников, занимающих первое место.
Прежде чем продолжить, позвольте мне напомнить читателю об изменении правил игры Jeopardy, касающемся ничьих после финального раунда. Теперь оба игрока не проходят дальше, а есть дополнительный вопрос для определения победителя в случае ничьей. Вот такая ситуация ...
Ситуация А
Пусть A = 10 000 долларов, а B = 4 000 долларов.
Игроку А не следует рисковать проигрышем, делая ставки не более A-2B-1. Если он не уверен в выигрыше в этой категории, он может поставить 0 долларов. В любом случае, он гарантирует себе победу. В этом случае А должен поставить от 0 до 1999 долларов.
У игрока B нет никаких шансов, если только игрок A не сделает слишком большую ставку и не проиграет. В этом случае игроку B следует учитывать результат третьего места и постараться удержаться выше него, если это возможно, выиграв 2000 долларов за второе место, а не 1000 долларов за третье.
Ситуация Б
Пусть A = 10 000 долларов, а B = 6 000 долларов.
Стратегия для А заключается в том, чтобы ожидать, что В поставит все свои деньги, и поставить достаточно, чтобы покрыть 2B, если он окажется прав. Однако, чтобы подстраховаться, он не должен ставить слишком много, чтобы в случае ошибки его ставка не оказалась ниже ставки В. В этом случае он должен поставить как минимум 2B-A+1 и AB-1. В этом случае диапазон ставок составляет от 2001 до 3999 долларов.
Стратегия для Б состоит в том, чтобы набрать как минимум достаточно средств, чтобы пройти тест А, если ответ будет верным, и тем самым повысить свой общий балл. В данном случае это 4001 и 6000 долларов.
Если оба игрока действуют, как ожидается, и следуют этой стратегии, то игрок B может выиграть только в том случае, если игрок A ошибается, а игрок B прав. Вероятность этого составляет около 19%.
Ситуация C
Здесь все усложняется и требует применения теории игр и рандомизации.
Пусть A = 10 000 долларов, а B = 7 000 долларов.
Прежде чем продолжить, важно оценить вероятность правильного ответа на вопрос в финальном раунде Jeopardy. В сезонах с 30 по 34 игрок, занявший первое место, ответил правильно в 52% случаев, а игрок, занявший второе место, — в 46%. Однако эти вероятности положительно коррелируют. Вот анализ всех четырех возможных вариантов:
- Оба варианта верны: 27%
- Первое место — правильно, второе — неправильно: 25%
- Первое место — неправильно, второе — правильно: 19%
- Оба варианта неверны на 29%.
Несмотря на то, что в игре Jeopardy средний процент правильных ответов первых двух игроков составляет 49%, вероятность того, что оба игрока ответят правильно или оба — неправильно, равна 56%.
Конечно, эти значения могут меняться в зависимости от категории, но давайте упростим задачу и воспользуемся приведенными выше вероятностями.
В этой ситуации игроку B не нужно зависеть от того, окажется ли A неправ, а B прав. Он может сделать небольшую ставку, скажем, 0 долларов, гарантируя себе выигрыш, если A окажется неправ. Другими словами, если A поставит достаточно, чтобы покрыть ставку B, если он окажется прав, то в случае ошибки он рискует оказаться ниже ставки B, а B поставит 0 долларов.
Однако, если А предсказывает, что В поставит низкую ставку, скажем, 0 долларов, то А может гарантировать себе победу, также поставив 0 долларов. По сути, у обоих игроков есть выбор: поставить низкую или высокую ставку. А должен хотеть поставить так же, как и В, а В — наоборот. Если бы оба игрока были идеальными логиками, они бы принимали решения случайным образом.
В этом случае высокая ставка со стороны А должна составлять от 2B-A+1 до AB-1, как и в ситуации B. В этом случае это 2999 и 4001 доллар. Низкая ставка со стороны А должна составлять 0 долларов.
Высокая ставка со стороны B должна быть такой же, как и в ситуации B: ставка должна быть достаточной, чтобы пройти мимо A, если предположение верно. В данном случае это 3001 и 7000 долларов. Низкая ставка со стороны B должна быть равна 0 долларов.
Простите, если я пропущу математические вычисления и сразу перейду к стратегиям рандомизации для обоих игроков.
Игрок А должен выбрать высокую ставку с вероятностью 62,3%, а низкую — с вероятностью 37,7%.
Вероятность выбора игрока B должна быть высокой (61,2%), а низкой (38,8%).
Если предположить, что оба игрока следуют этой стратегии рандомизации и что вероятности правильных ответов указаны выше, то вероятность выигрыша игрока А составляет 65,2%.
Если бы у игрока А было более 2/3 очков, чем у игрока В, вероятность его победы возросла бы до 81,0%.
Оба игрока должны помнить о значении правила 2/3 при совершении ставок в игре Double Jeopardy.