На этой странице
Как определяется преимущество казино по каждой ставке
Введение
Добро пожаловать в приложение по игре в крэпс. Здесь я вычисляю преимущество игрока для всех основных ставок в крэпсе. Вне этого приложения я обычно говорю о преимуществе казино, которое просто является произведением преимущества игрока и -1. Чтобы избежать умножения на -1 для каждой ставки, я буду говорить обо всем через преимущество игрока, которое, как вы можете ожидать, будет отрицательным, поскольку казино в конечном итоге имеет преимущество по всем ставкам, кроме бесплатных ставок. Пожалуйста, останьтесь ненадолго и проработайте некоторые ставки самостоятельно. Это не только даст вам более глубокое понимание вероятностей, но и, надеюсь, побудит вас освежить или улучшить свои математические навыки.
Прежде чем продолжить, необходимо понимать вероятность выпадения каждой суммы за один бросок. Это подробно объяснено на моей странице, посвященной основам вероятности в бросках игральных костей . Если вы не знали или не можете понять, что вероятность выпадения шестерки составляет 5/36, то посещение этой страницы является обязательным условием для ознакомления с данной страницей.
Общая формула для расчета ожидаемой доходности ставки выглядит следующим образом:
∑ (вероятность события i) × (возврат события i) по всем возможным исходам.
Преимущество игрока — это ожидаемая прибыль, деленная на первоначальную ставку. Например, при ставке против линии на спортивное событие вам нужно поставить 11 долларов, чтобы выиграть 10 долларов. Предполагая 50% вероятность выигрыша, ожидаемая прибыль составит 0,5 × (10) + 0,5 × (-11) = -0,5. Преимущество игрока составит -0,5/11 = -1/22 ≈ -4,545%.
Исключением из правила преимущества казино является случай, когда возможна ничья. Как правило, ничьи игнорируются при расчете преимущества казино. Чтобы это учесть, в случае возможной ничьи, ожидаемый выигрыш делится на среднюю сумму разрешенной ставки. «Средняя сумма разрешенной ставки» — это произведение первоначальной ставки и вероятности того, что ставка была разрешена. В крэпсе ничья возможна только при ставках «не пас» и «не приходит».
В крэпсе многие ставки выигрывают, если одно событие происходит раньше другого. Для разрешения таких ставок может потребоваться несколько бросков или даже больше. Если ставка выигрывает с вероятностью p, проигрывает с вероятностью q и остается активной с вероятностью 1-pq, то вероятность выигрыша в конечном итоге равна:
∑ p×(1-pq) i (для i=0 до бесконечности) =
p × (1/(1-(1-pq))) = p × (1/(p+q)) = p/(p+q).
На этой странице вы увидите множество выражений вида p/(p+q). Для экономии места я не буду каждый раз выводить выражение, поскольку оно уже приведено выше.
Проходи/Приходи
Вероятность выигрыша при первом броске составляет pr(7)+pr(11) = 6/36 + 2/36 = 8/36.
Вероятность установления точки и последующей победы равна pr(4)×pr(4 до 7) + pr(5)×pr(5 до 7) + pr(6)×pr(6 до 7) + pr(8)×pr(8 до 7) + pr(9)×pr(9 до 7) + pr(10)×pr(10 до 7) =
(3/36)×(3/9) + (4/36)×(4/10) + (5/36)×(5/11) + (5/36)×(5/11) + (4/36)×(4/10) + (3/36)×(3/9) =
(2/36) × (9/9 + 16/10 + 25/11) =
(2/36) × (990/990 + 1584/990 + 2250/990) =
(2/36) × (4824/990) = 9648/35640
Общая вероятность выигрыша составляет 8/36 + 9648/35640 = 17568/35640 = 244/495
Вероятность проигрыша, очевидно, равна 1 - (244/495) = 251/495
Таким образом, преимущество игрока составляет (244/495)×(+1) + (251/495)×(-1) = -7/495 ≈ -1,414%.
Не проходи/Не приходи
Вероятность выигрыша при первом броске равна pr(2)+pr(3) = 1/36 + 2/36 = 3/36.
Вероятность ничьей при первом броске составляет pr(12) = 1/36.
Вероятность установления точки и последующего выигрыша равна pr(4)×pr(7 до 4) + pr(5)×pr(7 до 5) + pr(6)×pr(7 до 6) + pr(8)×pr(7 до 8) + pr(9)×pr(7 до 9) + pr(10)×pr(7 до 10) =
(3/36)×(6/9) + (4/36)×(6/10) + (5/36)×(6/11) + (5/36)×(6/11) + (4/36)×(6/10) + (3/36)×(6/9) =
(2/36) × (18/9 + 24/10 + 30/11) =
(2/36) × (1980/990 + 2376/990 + 2700/990) =
(2/36) × (7056/990) = 14112/35640
Суммарная вероятность выигрыша составляет 3/36 + 14112/35640 = 17082/35640 = 2847/5940
Вероятность проигрыша равна 1-(2847/5940 + 1/36) = 1-(3012/5940) = 2928/5940
Ожидаемая доходность составляет 2847/5940×(+1) + 2928/5940×(-1) = -81/5940 = -3/220 ≈ 1,364%
Большинство других источников по игре в крэпс утверждают, что преимущество казино на ставке «не пас» составляет 1,403%. Причина расхождения заключается в том, следует ли учитывать ничьи. Я предпочитаю учитывать ничьи как денежную ставку, а другие — нет. Я не говорю, что одна сторона права или неправа, просто я предпочитаю их учитывать.Если ничья не считается денежной ставкой, то следует разделить указанную выше цифру на вероятность выигрыша или проигрыша по ставке (35/36). Таким образом, 1,364%/(35/36) ≈ -1,403%. Это преимущество казино при условии, что игрок никогда не выбросит 12 при первом броске.
Делайте ставки на победу
Сделайте ставку на 6 или 8: [(5/11)×7 + (6/11)×(-6)]/6 = (-1/11)/6 = -1/66 ≈ -1,515%
Сделайте ставку на 5 или 9: [(4/10)×7 + (6/10)×(-5)]/5 = (-2/10)/5 = -1/25 = -4,000%
Сделайте ставку на 4 или 10: [(3/9)×9 + (6/9)×(-5)]/5 = (-3/9)/5 = -1/15 ≈ -6,667%
Сделайте ставки на проигрыш
Ставка на проигрыш при выпадении 6 или 8: [(6/11)×4 + (5/11)×(-5)]/5 = (-1/11)/5 = -1/55 ≈ -1,818%
Ставка на проигрыш при выпадении 5 или 9: [(6/10)×5 + (4/10)×(-8)]/8 = (-2/10)/8 = -1/40 = -2,500%
Ставка на проигрыш при выпадении 4 или 10: [(6/9)×5 + (3/9)×(-11)]/11 = (-3/9)/11 = -1/33 ≈ -3,030%
Примечание: Эти ставки запрещены в наземных казино. Они доступны только в некоторых интернет-казино.
Купить
Купите ставку на 6 или 8: [(5/11)×23 + (6/11)×(-21)]/21 = (-11/11)/21 = -1/21 ≈ -4,762%
Купите ставку на 5 или 9: [(4/10)×29 + (6/10)×(-21)]/21 = (-10/10)/21 = -1/21 = -4,762%
Ставка на 4 или 10: [(3/9)×39 + (6/9)×(-21)]/21 = (-9/9)/21 = -1/21 ≈ -4,762%
Класть
Ставка против проигрыша на 6 или 8: [(6/11)×19 + (5/11)×(-25)]/25 = (-11/11)/25 = -1/25 ≈ -4,000%
Ставка против проигрыша на 5 или 9: [(6/10)×19 + (4/10)×(-31)]/31 = (-10/10)/31 = -1/31 = -3,226%
Ставка против проигрыша при выпадении 4 или 10: [(6/9)×19 + (3/9)×(-41)]/41 = (-9/9)/41 = -1/41 ≈ -2,439%
Большая шестерка/Большая восьмерка
[(5/11)×1 + (6/11)×(-1)]/1 = -1/11 ≈ 9,091%
Сложный 4/Сложный 10
Примечание: Выигрыш за жёсткие 4 и 10 составляет 7 к 1 или 8 к 1. В крэпсе коэффициенты на сукне указываются в соотношении 1 к 1, включая графическое изображение выше.
Вероятность выпадения «четверки» при любом броске составляет 1/36.
Вероятность выпадения цифры 7 при любом броске составляет 6/36.
Вероятность выпадения «мягкой» четверки при любом броске составляет 2/36 (1+3 и 3+1).
Вероятность выигрыша при любом броске составляет 1/36.
Вероятность проигрыша при любом броске составляет 6/36 + 2/36 = 8/36.
Вероятность выигрыша пари равна p/(p+q) (см. выше) = (1/36)/(9/36) = 1/9
Ожидаемая доходность составляет (1/9)×7 + (8/9)×(-1) = -1/9 ≈ 11,111%.
Преимущество игрока также составляет -1/9, поскольку ставка равна 1 единице.
Шансы получить твердую десятку такие же.
Сложный 6/Сложный 8
Примечание: Выигрыш за жёсткие 4 и 10 составляет 9 к 1, или 10 к 1. В крэпсе шансы на сукне указываются в соотношении 1 к 1, включая графическое изображение выше.
Вероятность выпадения шестерки при любом броске составляет 1/36.
Вероятность выпадения цифры 7 при любом броске составляет 6/36.
Вероятность выпадения «мягкой» шестерки при любом броске составляет 4/36 (1+5, 2+3, 3+2 и 5+1).
Вероятность выигрыша при любом броске составляет 1/36.
Вероятность проигрыша при любом броске составляет 6/36 + 4/36 = 10/36.
Вероятность выигрыша пари равна p/(p+q) (см. выше) = (1/36)/(11/36) = 1/11
Ожидаемая доходность составляет (1/11)×9 + (10/11)×(-1) = -1/11 ≈ 9,091%.
Преимущество игрока также составляет -1/11, поскольку ставка равна 1 единице.
Вероятность выпадения сложной восьмерки одинакова.
Крэпс 2/Крэпс 12
[(1/36)×30 + (35/36)×(-1)]/1 = -5/36 ≈ -13,889%
Крэпс 3/Крэпс 11
[(2/36)×15 + (34/36)×(-1)]/1 = -4/36 ≈ -11,111%
Любая игра в кости
[(4/36)×7 + (32/36)×(-1)]/1 = -4/36 ≈ -11,111%
Любые 7
[(6/36)×4 + (30/36)×(-1)]/1 = -6/36 ≈ -16,667%
Рог
Вероятность выпадения числа 2 или 12 составляет 1/36 + 1/36 = 2/36.
Вероятность выпадения числа 3 или 11 составляет 2/36 + 2/36 = 4/36.
Вероятность выпадения чего-либо другого составляет 1-2/36-4/36 = 30/36.
Помните, что ставка на «рог» — это как все четыре ставки в крэпсе в одной. Даже если одна из них выигрывает, остальные три всё равно проигрывают. Преимущество казино составляет:
[(2/36)×27 + (4/36)×12 + (30/36)×(-4)]/4 = (-18/36)/4 = 12,500%
Поле
Когда ставка 12 выплачивает в соотношении 2:1, ожидаемая доходность составляет:
2×(pr(2)+pr(12)) + 1×(pr(3)+pr(4)+pr(5)+pr(10)+pr(11)) + -1×(pr(6)+pr(7)+pr(8)+pr(9)) =
2×(1/36 + 1/36) + 1×(2/36 + 3/36 + 4/36 + 3/36 + 2/36) + -1×(5/36 + 6/36 + 5/36 + 4/36) =
2×(2/36) + 1×(14/36) + -1×(20/36) = -2/36 = -1/18 ≈ 5,556%.
Когда ставка 12 выплачивает 3:1, ожидаемая доходность составляет:
3×pr(2) + 2×pr(12)) + 1×(pr(3)+pr(4)+pr(5)+pr(10)+pr(11)) + -1×(pr(6)+pr(7)+pr(8)+pr(9)) =
3×(1/36) + 2×(1/36) + 1×(2/36 + 3/36 + 4/36 + 3/36 + 2/36) + -1×(5/36 + 6/36 + 5/36 + 4/36) =
3×(1/36) + 2×(1/36) + 1×(14/36) + -1×(20/36) = -1/36 ≈ 2,778%.
Вероятность покупки
4 и 10: [(3/9)×2 + (6/9)×(-1)]/1 = 0,000%
5 и 9: [(4/10)×3 + (6/10)×(-2)]/2 = 0,000%
6 и 8: [(5/11)×6 + (6/11)×(-5)]/5 = 0,000%
Коэффициенты ставок
4 и 10: [(6/9)×1 + (3/9)×(-2)]/1 = 0,000%
5 и 9: [(6/10)×2 + (4/10)×(-3)]/2 = 0,000%
6 и 8: [(6/11)×5 + (5/11)×(-6)]/5 = 0,000%
Совокупные коэффициенты на пропуск и покупку
Преимущество игрока на комбинированной линии «пас» и «покупка» определяется как средний выигрыш игрока, деленный на среднюю ставку игрока. Выигрыш на линии «пас» всегда равен -7/495, а выигрыш на линии «коэффициенты» всегда равен 0. Ожидаемая ставка зависит от того, какое количество коэффициентов вам разрешено. Предположим, что установлены полные двойные коэффициенты, или что ставка на линию «пас» составляет 2 доллара, ставка на коэффициенты на 4, 5, 9 и 10 составляет 4 доллара, а ставка на коэффициенты на 6 или 8 — 5 долларов.
Средний прирост составляет -2×(7/495) = -14/495.
Средняя ставка равна 2 + (3/36)×4 + (4/36)×4 + (5/36)×5 + (5/36)×5 + (4/36)×4 + (3/36)×4] =
2 + 106/36 = 178/36
Преимущество игрока составляет (-14/495)/(178/36) = -0,572%.
Общая формула, если можно взять x раз нечетные числа 6 и 8, y раз нечетные числа 5 и 9 и z раз нечетные числа 4 и 10, выглядит так: (-7 / 495) / [ 1 + ((5x + 4y + 3z) / 18) ]
Совокупные коэффициенты «Не пас» и «Против»
Преимущество игрока по комбинированным ставкам на «непрохождение» и «против» определяется как средний выигрыш игрока, деленный на среднюю ставку игрока. Выигрыш по ставке на «непрохождение» всегда равен -3/220, а выигрыш по ставкам на коэффициенты всегда равен 0. Ожидаемая ставка зависит от того, какое кратное значение коэффициентов вам разрешено. Предположим, что коэффициенты удвоены, а ставка на «непрохождение» составляет 10 долларов. Тогда игрок может поставить против коэффициентов 40 долларов, получив выигрыш в 20 долларов на 4 и 10, 30 долларов, получив выигрыш в 20 долларов на 5 и 9, и 24 доллара, получив выигрыш в 20 долларов на 6 и 8. Средний выигрыш составляет -10 × (3/220) = -30/220.
Средняя ставка составляет 10 + 2×[(3/36)×40 + (4/36)×30 + (5/36)×24] = 30.
Преимущество игрока составляет (-30/220)/30 = -0,455%.
Общая формула: если вы можете купить ставку с коэффициентом x, то преимущество казино на комбинированные ставки "не проходит" и "против" составляет (3/220)/(1+x).
Чистая прибыль/убыток за сессию
Приведенная ниже диаграмма показывает чистый выигрыш или проигрыш, который вы можете ожидать за 100 попыток или бросков кубиков. Для целей составления диаграммы игрок ставит 1 доллар на линию «Pass» и получает полные двойные шансы.
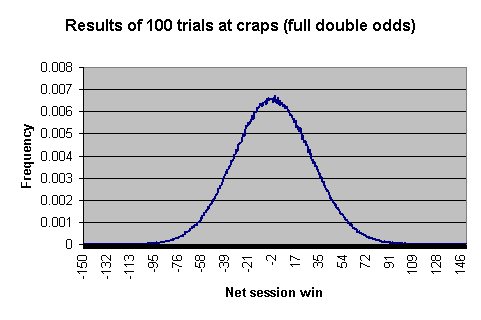
Вот несколько реальных цифр, показывающих вероятность попадания в различные интервалы.
Победа/Поражение в сессии
| Интервал | Вероятность |
|---|---|
| потеря более 100 долларов | 0,0422% |
| убыток в размере 76-100 долларов | 0,6499% |
| убыток в размере 51-75 долларов | 4,6414% |
| убыток в размере 26-50 долларов | 16.3560% |
| убыток от 1 до 25 долларов | 30,0583% |
| точка безубыточности | 0,6743% |
| выигрыш от 1 до 25 долларов | 28,6368% |
| выигрыш от 26 до 50 долларов | 14,4257% |
| выигрыш $51-$75 | 3,9097% |
| выигрыш $76-$100 | 0,5639% |
| выигрыш более 100 долларов | 0,0418% |
График и таблица были созданы путем моделирования 1 000 000 сессий по 100 испытаний, или первых бросков кубиков, и составления таблицы результатов каждой сессии.
Внутренние ссылки
- Вкратце, как рассчитывается преимущество казино по каждой ставке .
- Преимущество казино по всем основным ставкам как в расчете на одну ставку, так и на весь раунд ставок.
- Эксперименты по контролю за игральными костями. Результаты двух экспериментов по ловкому броску игральных костей.
- Преимущество в контроле над кубиками. Преимущество игрока, предполагающее, что он может влиять на результаты бросков кубиков.
- Варианты игры в крэпс . Альтернативные правила и ставки, такие как «Огненная ставка», «Крэпс без крэпса» и «Карточный крэпс».
- Калифорнийский крэпс . Как играют в крэпс в Калифорнии с использованием игральных карт.
- Игра в крэпс . Игра в крэпс с использованием карт в казино Viejas в Сан-Диего.
- Таблица количества бросков . Вероятность того, что стрелок продержится от 1 до 200 бросков, прежде чем выпадет семь очков.
- Спросите Волшебника. Посмотрите ответы на мои вопросы по игре в кости:
- Простая игра в крэпс. Моя простая игра в крэпс на Java.


