На этой странице
Почему количество колод имеет значение в блэкджеке
Введение
Любой авторитетный источник по блэкджеку подтвердит наличие положительной корреляции между количеством колод, используемых в блэкджеке, и преимуществом казино, при прочих равных условиях. Другими словами, чем меньше колод, тем выше шансы для игрока-любителя. Этот факт общеизвестен среди игроков в блэкджек, которые, по крайней мере, достаточно хорошо разбираются в игре, чтобы выбирать игры с хорошими правилами. Однако я никогда не встречал подробного объяснения того, почему это так. Цель этой статьи — пролить свет на этот вопрос.
Прежде чем начать, позвольте мне установить несколько базовых правил. Они были выбраны максимально реалистичными, учитывая условия игры в блэкджек на момент написания этой статьи в 2020 году:
- Дилер набрал 17 очков, что является слабым результатом.
- Выплаты по блэкджеку составляют 3 к 2.
- Дилер высматривает блэкджек, если у него открыта десятка или туз.
- Игрок может удвоить ставку на любые две карты.
- Игрок не может сдаться.
- Игрок может удвоить свой результат после разделения поля.
- Игрок может повторно разделить любую пару (включая тузы) до трех раз.
- Используется устройство непрерывного перемешивания карт (карты перемешиваются после каждой раздачи).
- Игрок использует базовую стратегию.
Мой калькулятор преимущества казино в блэкджеке показывает, что при данных правилах преимущество казино составляет следующее в зависимости от количества колод:
Преимущество казино в блэкджеке по колодам
| Палубы | Край дома |
|---|---|
| 1 | 0,014% |
| 2 | 0,341% |
| 4 | 0,499% |
| 6 | 0,551% |
| 8 | 0,577% |
Эти данные могут не совсем совпадать с другими авторитетными источниками по блэкджеку. Я считаю, что любые расхождения могут быть обусловлены либо использованием разделительной карты, либо применением игроком оптимальной стратегии, зависящей от состава колоды. В сравнении с этим, я предполагаю, что карты перемешиваются после каждой раздачи, и игрок всегда следует базовой стратегии, зависящей от общего количества карт.
Обратите внимание, что разница в преимуществе казино составляет 0,563% между восемью и одной палубой. В этой статье мы попытаемся ответить на вопрос, почему количество палуб оказывает такое существенное влияние на шансы выигрыша.
Сбалансированная игра
В качестве отправной точки я рассматриваю упрощенную игру в блэкджек, в которой правила абсолютно одинаковы как для игрока, так и для дилера, что приводит к нулевому преимуществу казино независимо от количества колод. Затем я постепенно добавляю фактические правила блэкджека, одно за другим, и изучаю, как они влияют на преимущество казино в зависимости от количества колод.
В исходной гипотетической упрощенной версии игры в блэкджек будут действовать те же правила, что и ранее, за исключением следующих моментов:
- Игрок следует стратегии «имитировать дилера».
- Выигрыш в блэкджеке оплачивается в равных суммах.
- Если и игрок, и дилер превышают лимит очков, то получается ничья.
Преимущество казино в этой сбалансированной игре, очевидно, составляет ровно 0,000%, поскольку каждое правило действует одинаково в обе стороны.
Позиционное преимущество дилера
Кто выигрывает в блэкджеке, когда и игрок, и дилер превышают лимит? Дилер. Другими словами, дилер обладает позиционным преимуществом, поскольку тот, кто первым превысил лимит, проигрывает, и игрок должен действовать первым. Именно поэтому дилер имеет преимущество, несмотря на многие правила, которые играют на руку игроку. Добавление этого правила к игре «Баланс» и моделирование с использованием одной и восьми колод приводит к следующим ожидаемым результатам для игрока.
Ожидаемые значения при изменении правил
| Правило | Одна палуба | Восемь палуб | Разница |
|---|---|---|---|
| Позиционное преимущество дилера | -8,237% | -8,157% | -0,079 % |
В таблице выше показано, что в этой гипотетической игре с одной колодой шансы игрока хуже, чем с восемью колодами. Это связано с тем, что с уменьшением количества колод вероятность перебора возрастает. Ниже приведена вероятность перебора в этой игре «имитация дилера», предполагающая, что дилер разыгрывает свою руку, даже если игрок переборщил первым.
- Одна колода = 27,333%
- Восемь колод = 27,209%
Приведенные выше данные показывают, что вероятность перебора у любой из сторон на 0,124% выше в игре с одной колодой по сравнению с игрой с восемью колодами. Существует некоторая корреляция между переборами у каждой стороны, поэтому давайте рассмотрим все четыре комбинации переборов у игрока и дилера:
Вероятности провала
| Бюст игрока | Разгром дилера | Одна палуба | Восемь палуб | Разница |
|---|---|---|---|---|
| Нет | Нет | 44,096% | 44,468% | -0,372% |
| Нет | Да | 19,095% | 19,051% | 0,044% |
| Да | Нет | 19,095% | 19,051% | 0,044% |
| Да | Да | 8,237% | 8,157% | 0,079% |
| Общий | 90,524% | 90,728% | -0,204% |
Причина, по которой вероятности не суммируются до 100%, заключается в том, что таблица не учитывает те раздачи, где у одной из сторон блэкджек, и раздача не была завершена каким-либо другим способом. Строка «Да, да» показывает ситуации, когда обе стороны перебрали, что привело к выигрышу дилера. Она показывает, что это происходит на 0,080% чаще в игре с одной колодой по сравнению с игрой с восемью колодами. Почему? Если одна из сторон перебрала, это должно было произойти после получения сильной руки от 12 до 16 очков. Эта рука должна была состоять как минимум из двух карт. В то же время, если у одной из сторон было две карты высокого достоинства, рука оставалась бы. Другими словами, получение дополнительной карты обычно происходит с руками, в которых карты меньше среднего достоинства. Удаление карт низкого достоинства в ситуациях получения дополнительной карты приводит к тому, что оставшиеся карты имеют избыток карт высокого достоинства. Этот эффект удаления карт низкого достоинства перед перебором более значителен в игре с одной колодой.
Выплата в блэкджеке составляет 3 к 2.
Следующее правило, которое мы добавим к сбалансированной игре, будет заключаться в том, что игрок, выигравший блэкджек, получает выплату 3 к 2. Добавление этого правила в мою симуляцию приводит к следующим совокупным ожидаемым доходам игроков.
- Одна колода = -5,912%
- Восемь колод = -5,894%
В таблице результатов моделирования, куда добавлена строка, отражающая добавление этого правила, отображается следующий вид:
Ожидаемые значения при изменении правил
| Правило | Одна палуба | Восемь палуб | Разница |
|---|---|---|---|
| Позиционное преимущество дилера | -8,237% | -8,157% | -0,079% |
| Выигрыш в блэкджеке приносит игроку выигрыш 3 к 2. | -5,912% | -5,894% | -0,018% |
Вычитание суммы в двух рядах показывает, какое преимущество получает игрок от выигрыша в блэкджеке при выплате 3 к 2:
- Одна колода = 2,325%
- Восемь колод = 2,263%
- Разница = 0,062%
Это легко проверить математически следующим образом. Пусть d = количество колод. Используя обозначения Excel, вероятность выигрыша в блэкджеке равна: вероятность(блэкджек игрока) * (1-вероятность(блэкджек дилера)) = (16*d)*(4*d)/комбинация(52*d,2) * [1-(16*d-1)*(4*d-1)/комбинация(52*d-2,2)
Вероятность выигрыша в блэкджеке
| Палубы | Вероятность |
|---|---|
| 1 | 4,649% |
| 2 | 4,578% |
| 4 | 4,544% |
| 6 | 4,532% |
| 8 | 4,527% |
Как показано выше, вероятность выигрыша в блэкджеке увеличивается с уменьшением количества колод. Это объясняется просто эффектом удаления карт. Например, предположим, что первая карта игрока — любая карта достоинством 10. Вероятность этого составляет 4/13, независимо от количества колод. Легко заметить, что в игре с одной колодой вероятность получить туз в качестве второй карты составляет 4/51 = 7,843%. В игре с восемью колодами эта вероятность составляет 32/415 = 7,711%, что на 0,123% меньше, чем в игре с одной колодой. Проще говоря, причина, по которой вероятность получения туза выше в игре с одной колодой, заключается в том, что колода становится богаче тузами после удаления из нее десятки. То же самое верно, если первая карта — туз; оставшиеся карты будут богаче десятками в игре с одной колодой.
Кроме того, если игрок получает блэкджек, вероятность того, что дилер получит его, снижается с уменьшением количества колод. Это происходит потому, что удаление игроком туза и десятки из колоды в игре с одной колодой значительно затрудняет дилеру получение блэкджека по сравнению с игрой с восемью колодами. В частности, вероятность блэкджека дилера, при условии, что у игрока он уже есть, составляет 3,673% при одной колоде и 4,605% при восьми колодах. Игрок выигрывает дополнительные полединицы с каждым выигрышным блэкджеком. Чтобы получить значение выигрышного блэкджека, выплачиваемого в соотношении 3 к 2 в нашей гипотетической сбалансированной игре, возьмите вероятность выигрышного блэкджека и умножьте ее на 0,5 за эти дополнительные полединицы каждый раз. В результате получается преимущество игрока в зависимости от количества колод, как показано ниже:
Преимущество игрока от выигрыша в блэкджеке
| Палубы | Преимущество игрока |
|---|---|
| 1 | 2,325% |
| 2 | 2,289% |
| 4 | 2,272% |
| 6 | 2,266% |
| 8 | 2,263% |
Обратите внимание, что математически рассчитанные выгоды от того, что выигравший игрок в блэкджек платит на полединицы больше, соответствуют результатам моделирования, показанным ранее для блэкджека с одной и восемью колодами.
В таблице ниже представлен постоянно обновляемый список проанализированных к настоящему моменту правил и их преимущества для игрока с одной колодой по сравнению с игроком с восемью колодами:
Влияние правил
| Правило | Преимущество однопалубного режима |
|---|---|
| Позиционное преимущество дилера | -0,079% |
| Выигрыш в блэкджеке приносит игроку выигрыш 3 к 2. | 0,062% |
| Общий | -0,018% |
Далее проанализируем выгоду для игрока от возможности остановиться на сумме от 12 до 16. Базовая стратегия, зависящая от суммы в этом диапазоне, одинакова для любого количества колод и выглядит следующим образом:
- При сумме очков 12, играйте против дилера с суммой очков от 4 до 6, в противном случае — берите ещё одну карту.
- При сумме очков от 13 до 16, играйте против дилера с суммой очков от 2 до 6, в противном случае — берите ещё одну карту.
Добавление этой стратегии в симуляцию приводит к следующим ожидаемым доходам игрока:
- Одна колода = -2,209%
- Восемь колод = -2,625%
В приведенной ниже таблице результатов моделирования есть строка, содержащая информацию о добавлении этого правила:
Ожидаемые значения при изменении правил
| Правило | Одна палуба | Восемь палуб | Разница |
|---|---|---|---|
| Позиционное преимущество дилера | -8,237% | -8,157% | -0,079% |
| Выигрыш в блэкджеке приносит игроку выигрыш 3 к 2. | -5,912% | -5,894% | -0,018% |
Разница между вторым и третьим рядом показывает эффект свободы воли игрока, позволяющей ему встать на твердую отметку от 12 до 16.
- Одна колода = 3,703%
- Восемь колод = 3,270%
- Разница = 0,433%
Вычитание этих двух цифр показывает, что эффект от изменения правил приносит игроку на 0,433% больше выигрыша в игре с одной колодой по сравнению с игрой с восемью колодами. Вопреки распространенному мнению, это объясняет большую часть причин, почему игра с одной колодой приносит игроку на 0,563% больше выигрыша, чем игра с восемью колодами.
Рассмотрим подробнее, что происходит, когда игрок останавливается при сумме очков от 12 до 16, в то время как дилер не может этого сделать. В этой таблице показана выгода для игрока от различных событий, которые изменяются из-за того, что игрок получает меньше очков при сумме очков, что приводит к меньшему количеству переборов у игрока и большему количеству переборов у дилера, а также к большему количеству проигрышей дилера в противостояниях:
Возможные исходы, когда игрок стоит на твердом поле от 12 до 16
| Событие | Одна палуба | Восемь палуб | Разница |
|---|---|---|---|
| Меньше арестов только с участием игроков. | 6,282% | 6,271% | 0,010% |
| Больше арестов, проводимых исключительно дилерами. | 4,228% | 4,171% | 0,057% |
| Меньше обоих бюстов | 4,228% | 4,172% | 0,055% |
| Игрок выигрывает меньше вбрасываний | -1,914% | -2,039% | 0,125% |
| Дилер выигрывает больше противостояний | -9,121% | -9,306% | 0,185% |
| Общий | 3,703% | 3,270% | 0,433% |
В таблице приведена упрощенная версия, демонстрирующая преимущество более частых выигрышей дилера из-за того, что он чаще проигрывает в противостояниях:
Кратко изложенные возможные исходы, когда игрок стоит на твердом поле с номерами от 12 до 16.
| Событие | Одна палуба | Восемь палуб | Разница |
|---|---|---|---|
| Игрок получает меньше выгоды | 14,738% | 14,615% | 0,123% |
| Поражение при вбрасывании | -11,035% | -11,345% | 0,310% |
| Общий | 3,703% | 3,270% | 0,433% |
Проще говоря, в игре с одной колодой игрок будет проигрывать на 14,738% реже, чем дилер, следуя базовой стратегии с суммой очков от 12 до 16. Однако в 75% случаев дилер не проигрывает, что приводит к его выигрышу в ситуации, когда у игрока сумма очков 16 или меньше, и он не может выиграть. По сравнению со всеми остальными раздачами, игрок экономит 14,738%, проигрывая реже, но теряет 11,035% в виде большего количества поражений в ситуациях, что в сумме дает чистый выигрыш в 3,703% в игре с одной колодой.
В игре с восемью колодами это преимущество составляет всего 3,270%. В целом, выгода от стратегического положения при выпадении от 12 до 16 карт приносит игроку на 0,433% больше в игре с одной колодой, чем в игре с восемью колодами.
Почему стратегическая остановка игры более ценна в игре с одной колодой, чем с восемью? Ответ аналогичен тому, почему позиционное преимущество дилера более значимо в игре с одной колодой. В игре с одной колодой чаще происходит перебор. Хотя перебор может быть как положительным, так и отрицательным, он больше вредит игроку, потому что он проигрывает, когда обе стороны делают перебор. В суммах от 12 до 16, когда игрок останавливается, скорее всего, больше мелких карт, чем крупных. Это оставляет больше старших карт в колоде, которые потенциально могут привести к перебору. Последствия удаления этих низких карт, необходимых игроку для улучшения своей руки, обходятся дороже в игре с одной колодой, чем в игре с восемью колодами. Другими словами, брать карты у слабых игроков в игре с одной колодой опаснее. Вместо этого остановка игры более выгодна в игре с одной колодой.
Ниже представлена обновленная таблица соотношения затрат и выгод от каждого изменения правил:
Влияние правил
| Правило | Преимущество однопалубного режима |
|---|---|
| Позиционное преимущество дилера | -0,079% |
| Выигрыш в блэкджеке приносит игроку выигрыш 3 к 2. | 0,061% |
| Игрок может стоять на твердом покрытии размером от 12 до 16. | 0,433% |
| Общий | 0,415% |
Игрок может удвоить ставку
Далее проанализируем выгоду для игрока от возможности удвоить выигрыш. Для изучения эффекта я использовал в симуляции соответствующую стратегию удвоения для заданного количества колод, которая описана далее в статье. Добавление этой стратегии в симуляцию приводит к следующим ожидаемым результатам для игрока:
- Одна колода = -0,556%
- Восемь колод = -1,245%
В таблице результатов моделирования есть строка, содержащая информацию о добавлении данного правила:
Ожидаемые значения при изменении правил
| Правило | Одна палуба | Восемь палуб | Разница |
|---|---|---|---|
| Позиционное преимущество дилера | -8,237% | -8,157% | -0,079% |
| Выигрыш в блэкджеке приносит игроку выигрыш 3 к 2. | -5,912% | -5,894% | -0,018% |
| Игрок может стоять на твердом покрытии размером от 12 до 16. | -2,209% | -2,625% | 0,415% |
| Игрок может удвоить ставку | -0,556% | -1,245% | 0,689% |
Разница между третьим и четвертым рядом показывает эффект наличия у игрока свободы воли для удвоения ставки, а именно:
- Одна колода = 1,653%
- Восемь колод = 1,380%
- Разница = 0,273%
Вычитание этих двух цифр показывает, что эффект от изменения правил приносит игроку на 0,273% больше выигрыша в игре с одной колодой по сравнению с игрой с восемью колодами. Это объясняет еще одну важную причину, почему игра с одной колодой приносит игроку на 0,563% больше выигрыша, чем игра с восемью колодами.
Почему удвоение ставки более выгодно в игре с одной колодой? В большинстве случаев игрок удваивает ставку при сумме очков от 9 до 11. Удвоение производится двумя картами, поэтому для достижения низкой суммы от 9 до 11 необходимо две карты меньшего номинала, чем обычно. Если из одной колоды карт удалить две карты меньшего номинала, вероятность того, что следующая карта будет десяткой, составляет 32%, что, очевидно, хорошо при удвоении ставки при сумме очков. В то же время, если из восьми колод удалить две карты меньшего номинала, эффект удаления будет не таким сильным, снижая вероятность того, что следующая карта будет десяткой, до 30,92%.
Ниже приведена обновленная таблица соотношения затрат и выгод от каждого изменения правил. Обратите внимание, что общая выгода в размере 0,689% превышает окончательную разницу в преимуществе казино. Это связано с тем, что мы еще не учли эффект разделения.
Влияние правил
| Правило | Преимущество однопалубного режима |
|---|---|
| Позиционное преимущество дилера | -0,079% |
| Выигрыш в блэкджеке приносит игроку выигрыш 3 к 2. | 0,061% |
| Игрок может стоять на твердом покрытии размером от 12 до 16. | 0,433% |
| Игрок может удвоить ставку | 0,273% |
| Общий | 0,689% |
Игрок может разделиться
Далее я проанализировал выгоду для игрока от возможности разделения колоды. Для изучения эффекта я использовал в симуляции соответствующую стратегию разделения для заданного количества колод, которая описана далее в статье. Добавление этой стратегии приводит нас к полной базовой стратегии. После добавления разделения колоды других различий в правилах между игроком и дилером, которые можно было бы изучить, нет. Ожидаемая доходность игрока при полной базовой стратегии составляет:
- Одна колода = -0,012%
- Восемь колод = -0,575%
В таблице результатов моделирования, включающей строку для добавления этого правила, содержится следующая информация:
Ожидаемые значения при изменении правил
| Правило | Одна палуба | Восемь палуб | Разница |
|---|---|---|---|
| Позиционное преимущество дилера | -8,237% | -8,157% | -0,079% |
| Выигрыш в блэкджеке приносит игроку выигрыш 3 к 2. | -5,912% | -5,894% | -0,018% |
| Игрок может стоять на твердом покрытии размером от 12 до 16. | -2,209% | -2,625% | 0,415% |
| Игрок может удвоить ставку | -0,556% | -1,245% | 0,689% |
| Игрок может разделить | -0,012% | -0,575% | 0,563% |
Разница между четвертым и пятым рядами показывает эффект наличия у игрока свободы воли для разделения.
- Одна колода = 0,544%
- Восемь колод = 0,669%
- Разница = -0,125%
Вычитание этих двух значений показывает, что эффект от изменения правил приносит игроку на 0,125% меньше пользы в игре с одной колодой по сравнению с игрой с восемью колодами.
В игре с восемью колодами разделение карт выгоднее, чем с одной, потому что вероятность получить пару на первых двух картах выше. Если говорить точнее, с восемью колодами вероятность составляет 13*combin(4*8,2)/combin(52*8,2) = 7,470%. С одной колодой вероятность составляет 13*combin(4*1,2)/combin(52*1,2) = 5,882%.
Напомним также, что базовые правила игры допускают повторное разделение карт до трех раз или до четырех раз. Если из одной колоды удаляются две карты одного ранга, вероятность получить эту карту на следующей составляет 2/50 = 4,000%. В то же время, для колоды из восьми карт эта вероятность составляет 30/414 = 7,246%. Поскольку в игре с одной колодой разделение и повторное разделение происходит реже, общая ценность разделения снижается. Это объясняет, почему выгода от разделения уменьшается при переходе от восьми колод к одной.
Добавление отрицательного эффекта разделения карт в игре с одной колодой завершает нашу таблицу влияния различных правил на преимущества игры с одной колодой по сравнению с игрой с восемью колодами.
Правила игры с одной колодой. Преимущества: Позиционное преимущество дилера -0,079%. Выигрыш в блэкджеке: выплата 3 к 2 -0,061%. Игрок может остановиться на картах от 12 до 16 -0,433%. Игрок может удвоить ставку -0,273%. Игрок может разделить карты -0,125%. Итого -0,563%.Обратите внимание, что сумма в нижней правой ячейке, равная 0,563%, совпадает с разницей, полученной с помощью калькулятора преимущества дома, цитируемого в начале статьи. Вот та же таблица, упорядоченная по степени влияния:
Влияние правил
| Правило | Преимущество однопалубного режима |
|---|---|
| Позиционное преимущество дилера | -0,079% |
| Выигрыш в блэкджеке приносит игроку выигрыш 3 к 2. | 0,061% |
| Игрок может стоять на твердом покрытии размером от 12 до 16. | 0,433% |
| Игрок может удвоить ставку | 0,273% |
| Игрок может разделить | -0,125% |
| Общий | 0,563% |
Таблицы базовых стратегий
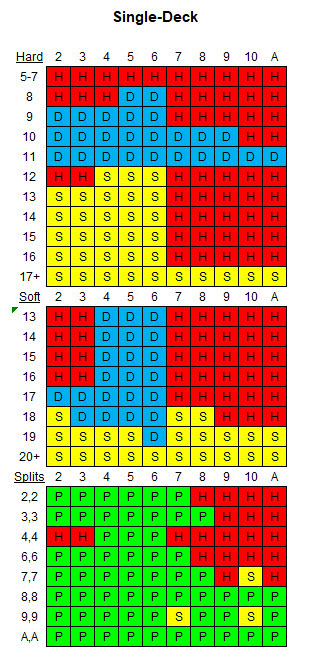
В следующей таблице представлена соответствующая базовая стратегия для данных правил и одной колоды.
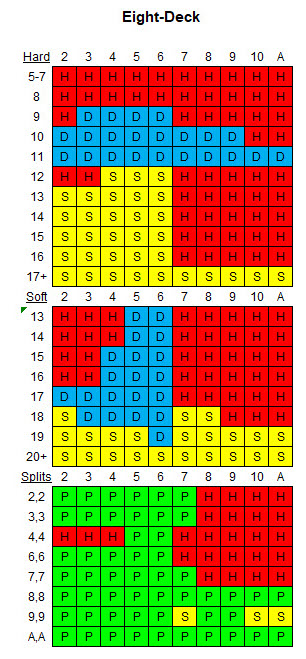
В следующей таблице представлена соответствующая базовая стратегия для данных правил и восьми колод.
Таблицы ожидаемых значений
В следующей таблице показано ожидаемое значение каждой начальной руки в игре с одной колодой. В верхней строке показана открытая карта дилера. Ожидаемые значения измеряются до того, как дилер проверит наличие блэкджека. В столбце «Итого» показано взвешенное среднее ожидаемых значений в каждой строке в зависимости от вероятности получения руки. В нижней правой ячейке показано ожидаемое значение всей игры.
Ожидаемые значения в игре с одной колодой
Ожидаемые значения для руки игрока и открытой карты дилера при наличии одной колоды
| Игрок | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Туз | Общий |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | -0.1278 | -0.0968 | -0.0379 | 0,0227 | 0,0403 | -0.1191 | -0.1805 | -0.2624 | -0.3654 | -0.5443 | -0.2169 |
| 6 | -0.1477 | -0.1037 | -0.0519 | 0,0104 | 0,0371 | -0.1640 | -0.2343 | -0.3046 | -0.4015 | -0.5713 | -0.2469 |
| 7 | -0.1120 | -0.0701 | -0.0119 | 0,0528 | 0,0683 | -0.0690 | -0.2232 | -0.2948 | -0.3863 | -0.5765 | -0.2211 |
| 8 | -0.0174 | 0,0199 | 0,0826 | 0.1407 | 0.1498 | 0.0921 | -0.0565 | -0.2135 | -0.3136 | -0.5144 | -0.1286 |
| 9 | 0.1124 | 0.1923 | 0.2837 | 0.3753 | 0.3799 | 0.1951 | 0.1111 | -0.0519 | -0.2165 | -0.4146 | 0,0151 |
| 10 | 0.4262 | 0.4908 | 0,5494 | 0.6276 | 0.6241 | 0.4458 | 0.3145 | 0.1644 | -0.0528 | -0.2991 | 0.2316 |
| 11 | 0,5428 | 0.5922 | 0.6516 | 0.7176 | 0.7198 | 0.4785 | 0.3417 | 0.2240 | 0,0670 | -0.1848 | 0.3268 |
| 12 | -0.2518 | -0.2255 | -0.1915 | -0.1364 | -0.1194 | -0.2273 | -0.2925 | -0.3639 | -0.4175 | -0.5824 | -0.3131 |
| 13 | -0.2879 | -0.2411 | -0.1816 | -0.1344 | -0.1208 | -0.2861 | -0.3461 | -0.3764 | -0.4590 | -0.6106 | -0.3415 |
| 14 | -0.2900 | -0.2391 | -0.1835 | -0.1342 | -0.1209 | -0.3442 | -0.3612 | -0.4192 | -0.4957 | -0.6356 | -0.3644 |
| 15 | -0.2803 | -0.2379 | -0.1837 | -0.1388 | -0.1266 | -0.3590 | -0.4133 | -0.4703 | -0.5397 | -0.6677 | -0.3893 |
| 16 | -0.2863 | -0.2446 | -0.1872 | -0.1435 | -0.1450 | -0.3760 | -0.4254 | -0.4797 | -0.5482 | -0.6739 | -0.3978 |
| 17 | -0.1568 | -0.1216 | -0.0712 | -0.0445 | -0.0306 | -0.1217 | -0.3976 | -0.4154 | -0.4562 | -0.6560 | -0.2947 |
| 18 | 0.1072 | 0.1359 | 0.1538 | 0.1983 | 0.2031 | 0.3887 | 0,0956 | -0.1961 | -0.2242 | -0.4527 | -0.0185 |
| 19 | 0.3763 | 0.3774 | 0.3965 | 0.4449 | 0,4364 | 0.6101 | 0.5769 | 0,2642 | 0,0125 | -0.1586 | 0,2644 |
| А,2 | 0,0402 | 0.0711 | 0.1174 | 0.2130 | 0,2455 | 0.1074 | 0,0392 | -0.0141 | -0.1454 | -0.3991 | -0.0057 |
| А,3 | 0,0184 | 0,0447 | 0.1127 | 0.2042 | 0.2391 | 0,0605 | 0,0349 | -0.0602 | -0.1781 | -0.4205 | -0.0308 |
| А,4 | -0.0103 | 0,0237 | 0,0892 | 0.1753 | 0.2191 | 0,0339 | -0.0354 | -0.1136 | -0.2226 | -0.4533 | -0.0697 |
| А,5 | -0.0298 | -0.0019 | 0,0667 | 0.1490 | 0.2327 | -0.0239 | -0.0842 | -0.1666 | -0.2760 | -0.4900 | -0.1094 |
| А,6 | 0,0142 | 0,0743 | 0.1549 | 0.2805 | 0.2630 | 0,0597 | -0.0646 | -0.1348 | -0.2383 | -0.4810 | -0.0586 |
| А,7 | 0.1279 | 0.1867 | 0.3091 | 0.3482 | 0.3623 | 0.4118 | 0.1209 | -0.0873 | -0.1926 | -0.4433 | 0,0459 |
| А,8 | 0.3953 | 0.4157 | 0.4100 | 0.4593 | 0.4666 | 0.6146 | 0.6078 | 0.2882 | -0.0009 | -0.1938 | 0.2686 |
| А,9 | 0,6525 | 0.6415 | 0.6507 | 0.6810 | 0.6730 | 0.7732 | 0.7848 | 0.7656 | 0.4594 | 0,0943 | 0.5871 |
| А,10 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.4081 | 1.0409 | 1.4449 |
| А,А | 0.6384 | 0.6863 | 0.7417 | 0.8075 | 0.8289 | 0.6277 | 0,4865 | 0.3605 | 0.2080 | -0.1580 | 0.4744 |
| 2,2 | -0.0349 | 0,0396 | 0.1235 | 0.3014 | 0.3378 | 0,0137 | -0.1412 | -0.2224 | -0.3355 | -0.5246 | -0.1145 |
| 3,3 | -0.1082 | -0.0209 | 0.1607 | 0.3049 | 0.3395 | -0.0448 | -0.2232 | -0.3100 | -0.3986 | -0.5715 | -0.1646 |
| 4,4 | -0.0136 | 0,0268 | 0.1354 | 0.2680 | 0.2980 | 0.1104 | -0.0549 | -0.2063 | -0.3069 | -0.5065 | -0.0991 |
| 5,5 | 0.4441 | 0,5075 | 0.5870 | 0.6933 | 0.7084 | 0.4663 | 0.3227 | 0.1738 | -0.0510 | -0.2978 | 0.2444 |
| 6,6 | -0.0963 | 0,0132 | 0.1456 | 0.2786 | 0.1992 | -0.1933 | -0.3222 | -0.3862 | -0.4366 | -0.5989 | -0.2245 |
| 7,7 | -0.0546 | 0,0494 | 0.1879 | 0.2244 | 0.2396 | -0.0524 | -0.3804 | -0.4744 | -0.5556 | -0.6790 | -0.2508 |
| 8,8 | 0.1165 | 0.1873 | 0,2245 | 0.3287 | 0.3508 | 0.3040 | -0.0599 | -0.4017 | -0.4929 | -0.6389 | -0.1224 |
| 9,9 | 0.2052 | 0.2156 | 0.3070 | 0.4064 | 0.4080 | 0.4011 | 0.2067 | -0.0986 | -0.2041 | -0.4520 | 0,0666 |
| 10,10 | 0.6220 | 0.6323 | 0.6402 | 0.6718 | 0.6683 | 0.7647 | 0.7832 | 0.7440 | 0.4539 | 0.1383 | 0.5803 |
| Общий | 0.1021 | 0.1388 | 0.1860 | 0.2391 | 0.2471 | 0.1473 | 0,0551 | -0.0435 | -0.1712 | -0.3891 | -0.0001 |
Ожидаемые значения в игре с восемью колодами
Ожидаемые значения карт в руке игрока и карты дилера при наличии восьми колод
| Игрок | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Туз | Общий |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | -0.1258 | -0.0929 | -0.0562 | -0.0175 | 0,018 | -0.1196 | -0.1871 | -0.266 | -0.3663 | -0.5291 | -0.2191 |
| 6 | -0.1389 | -0.1042 | -0.0677 | -0.0287 | 0,0085 | -0.1534 | -0.2192 | -0.2941 | -0.3902 | -0.5469 | -0.2395 |
| 7 | -0.1094 | -0.0760 | -0.0391 | -0.0004 | 0,0349 | -0.0689 | -0.2121 | -0.2866 | -0.3731 | -0.5526 | -0.2164 |
| 8 | -0.0234 | 0,0076 | 0,0427 | 0,0774 | 0.1079 | 0,0831 | -0.0595 | -0.2104 | -0.3079 | -0.4931 | -0.1316 |
| 9 | 0,0743 | 0.1277 | 0.1921 | 0.2580 | 0.3141 | 0.1745 | 0,0998 | -0.0522 | -0.2180 | -0.3962 | -0.0071 |
| 10 | 0.3653 | 0.4176 | 0.4704 | 0,5253 | 0.5723 | 0.3990 | 0,2895 | 0.1469 | -0.0535 | -0.2865 | 0.2056 |
| 11 | 0.4786 | 0,5264 | 0,5759 | 0.6271 | 0.6718 | 0,4653 | 0.3496 | 0.2271 | 0,0864 | -0.2297 | 0.3097 |
| 12 | -0.2535 | -0.2331 | -0.2041 | -0.1613 | -0.1208 | -0.2146 | -0.2741 | -0.3430 | -0.4273 | -0.5746 | -0.3146 |
| 13 | -0.2867 | -0.2461 | -0.2030 | -0.1611 | -0.1210 | -0.2713 | -0.3264 | -0.3858 | -0.4682 | -0.6049 | -0.3447 |
| 14 | -0.2870 | -0.2456 | -0.2034 | -0.1612 | -0.1211 | -0.3240 | -0.3707 | -0.4295 | -0.5059 | -0.6328 | -0.3694 |
| 15 | -0.2858 | -0.2456 | -0.2033 | -0.1616 | -0.1217 | -0.3683 | -0.4162 | -0.4715 | -0.5422 | -0.6597 | -0.3927 |
| 16 | -0.2866 | -0.2463 | -0.2038 | -0.1622 | -0.1236 | -0.4103 | -0.4547 | -0.5057 | -0.5721 | -0.6820 | -0.4128 |
| 17 | -0.1565 | -0.1205 | -0.0819 | -0.0461 | -0.0090 | -0.1085 | -0.3842 | -0.4223 | -0.4633 | -0.6636 | -0.2958 |
| 18 | 0.1098 | 0.1379 | 0.1648 | 0.1953 | 0.2211 | 0.3982 | 0.1045 | -0.1847 | -0.2394 | -0.4626 | -0.0208 |
| 19 | 0.3780 | 0.3949 | 0.4138 | 0.4372 | 0.4513 | 0.6153 | 0.5918 | 0,2848 | -0.0149 | -0.1753 | 0,2569 |
| А,2 | 0,0458 | 0,0737 | 0.1041 | 0.1376 | 0.2024 | 0.1207 | 0,0523 | -0.0350 | -0.1703 | -0.3789 | -0.0269 |
| А,3 | 0,0224 | 0,0507 | 0,0827 | 0.1366 | 0.2010 | 0,0769 | 0,0155 | -0.0733 | -0.2024 | -0.4031 | -0.0533 |
| А,4 | -0.0006 | 0,0294 | 0,0641 | 0.1328 | 0.1986 | 0,0368 | -0.0282 | -0.1123 | -0.2357 | -0.4281 | -0.0803 |
| А,5 | -0.0211 | 0,0088 | 0,0611 | 0.1301 | 0.2004 | -0.0070 | -0.0689 | -0.1507 | -0.2691 | -0.4532 | -0.1057 |
| А,6 | -0.0006 | 0,0558 | 0.1220 | 0.1933 | 0,2513 | 0,0545 | -0.0721 | -0.1479 | -0.2563 | -0.4626 | -0.0792 |
| А,7 | 0.1160 | 0.1749 | 0.2418 | 0.3000 | 0.3560 | 0.4014 | 0.1074 | -0.0990 | -0.2075 | -0.4205 | 0,0270 |
| А,8 | 0.3800 | 0.3993 | 0.4157 | 0.4389 | 0.4621 | 0.6159 | 0,5953 | 0.2878 | -0.0164 | -0.1795 | 0,2579 |
| А,9 | 0.6371 | 0.6455 | 0.6562 | 0.6699 | 0.6778 | 0.7732 | 0.7909 | 0.7591 | 0.4379 | 0.1070 | 0,5752 |
| А,10 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.3874 | 1.0388 | 1.4309 |
| А,А | 0.6072 | 0.6561 | 0.7062 | 0.7588 | 0.8058 | 0.6277 | 0.5001 | 0.3629 | 0.2059 | -0.1511 | 0.4411 |
| 2,2 | -0.0797 | -0.0089 | 0,0697 | 0.1700 | 0,2643 | 0,0087 | -0.1576 | -0.2385 | -0.3430 | -0.5115 | -0.1430 |
| 3,3 | -0.1305 | -0.0482 | 0,0500 | 0.1502 | 0,2425 | -0.0518 | -0.2189 | -0.2946 | -0.3899 | -0.5465 | -0.1859 |
| 4,4 | -0.0225 | 0,0080 | 0,0441 | 0.1066 | 0.2027 | 0,0857 | -0.0595 | -0.2096 | -0.3070 | -0.4921 | -0.1212 |
| 5,5 | 0.3676 | 0.4201 | 0.4748 | 0,5324 | 0,5814 | 0.4012 | 0.2910 | 0.1477 | -0.0534 | -0.2863 | 0.2074 |
| 6,6 | -0.1947 | -0.0972 | 0,0043 | 0.1075 | 0.1900 | -0.2189 | -0.2775 | -0.3453 | -0.4295 | -0.5767 | -0.2426 |
| 7,7 | -0.1233 | -0.0335 | 0,0669 | 0.1569 | 0.2508 | -0.0485 | -0.3765 | -0.4361 | -0.5129 | -0.6382 | -0.2497 |
| 8,8 | 0.0720 | 0.1452 | 0.2171 | 0.3005 | 0.3753 | 0.3195 | -0.0276 | -0.3893 | -0.5170 | -0.6660 | -0.1329 |
| 9,9 | 0.1943 | 0.2506 | 0.3196 | 0.3925 | 0.4551 | 0.3996 | 0.2308 | -0.0801 | -0.2369 | -0.4624 | 0,0585 |
| 10,10 | 0.6334 | 0.6442 | 0,6549 | 0.6688 | 0.6770 | 0.7723 | 0.7907 | 0.7566 | 0.4373 | 0.1124 | 0,5745 |
| Общий | 0,0927 | 0.1262 | 0.1628 | 0.2025 | 0.2390 | 0.1453 | 0,0585 | -0.0403 | -0.1727 | -0.3712 | -0.0058 |
Разница в ожидаемом значении (в %)
В следующей таблице показано ожидаемое значение в игре с одной колодой за вычетом значения в игре с восемью колодами в процентном соотношении.
Изменение ожидаемых значений в зависимости от руки игрока и открытой карты дилера (x100)
| Игрок | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Туз | Общий |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | -0.196 | -0.383 | 1.834 | 4.02 | 2.229 | 0,05 | 0,664 | 0,361 | 0,087 | -1.52 | 0,22 |
| 6 | -0.8770 | 0,0480 | 1.5840 | 3.9030 | 2.8630 | -1.0640 | -1.5170 | -1.0490 | -1.1320 | -2.4330 | -0.7380 |
| 7 | -0.2560 | 0.5920 | 2.7210 | 5.3240 | 3.3400 | -0.0070 | -1.1090 | -0.8160 | -1.3150 | -2.3840 | -0.4720 |
| 8 | 0.6060 | 1.2300 | 3.9870 | 6.3300 | 4.1900 | 0.9040 | 0.3020 | -0.3070 | -0.5740 | -2.1370 | 0.2910 |
| 9 | 3.8080 | 6.4600 | 9.1610 | 11.7320 | 6.5770 | 2.0670 | 1.1320 | 0.0300 | 0.1480 | -1.8380 | 2.2220 |
| 10 | 6.0970 | 7.3170 | 7.8980 | 10.2270 | 5.1830 | 4.6820 | 2.4980 | 1.7530 | 0.0720 | -1.2510 | 2.6040 |
| 11 | 6.4200 | 6.5830 | 7.5650 | 9.0560 | 4.8030 | 1.3220 | -0.7900 | -0.3170 | -1.9460 | 4.4940 | 1.7050 |
| 12 | 0.1670 | 0.7540 | 1.2640 | 2.4890 | 0.1350 | -1.2760 | -1.8390 | -2.0880 | 0.9840 | -0.7830 | 0.1460 |
| 13 | -0.1260 | 0.5070 | 2.1460 | 2.6670 | 0,0210 | -1.4780 | -1.9700 | 0.9410 | 0.9190 | -0.5660 | 0.3180 |
| 14 | -0.2970 | 0.6510 | 1.9930 | 2.6980 | 0,0150 | -2.0210 | 0.9460 | 1.0330 | 1.0240 | -0.2860 | 0.5000 |
| 15 | 0.5560 | 0.7690 | 1.9570 | 2.2820 | -0.4950 | 0.9270 | 0.2900 | 0.1190 | 0.2470 | -0.7990 | 0.3400 |
| 16 | 0.0300 | 0.1700 | 1.6680 | 1.8640 | -2.1330 | 3.4380 | 2.9220 | 2.6000 | 2.3870 | 0.8060 | 1.4950 |
| 17 | -0.0300 | -0.1100 | 1.0720 | 0.1630 | -2.1630 | -1.3190 | -1.3380 | 0.6910 | 0.7130 | 0.7580 | 0.1060 |
| 18 | -0.2560 | -0.2000 | -1.0990 | 0.2950 | -1.7950 | -0.9490 | -0.8890 | -1.1420 | 1.5210 | 0.9900 | 0.2340 |
| 19 | -0.1730 | -1.7470 | -1.7360 | 0.7660 | -1.4910 | -0.5200 | -1.4980 | -2.0590 | 2.7370 | 1.6770 | 0.7460 |
| А,2 | -0.5660 | -0.2590 | 1.3280 | 7.5340 | 4.3080 | -1.3290 | -1.3120 | 2.0900 | 2.4910 | -2.0210 | 2.1220 |
| А,3 | -0.4090 | -0.6000 | 3.0040 | 6.7580 | 3.8040 | -1.6410 | 1.9440 | 1.3040 | 2.4300 | -1.7440 | 2.2470 |
| А,4 | -0.9750 | -0.5720 | 2.5100 | 4.2580 | 2.0490 | -0.2980 | -0.7230 | -0.1290 | 1.3080 | -2.5210 | 1.0610 |
| А,5 | -0.8730 | -1.0720 | 0.5650 | 1.8950 | 3.2330 | -1.6930 | -1.5280 | -1.5890 | -0.6930 | -3.6740 | -0.3690 |
| А,6 | 1.4820 | 1.8480 | 3.2870 | 8.7240 | 1.1650 | 0.5180 | 0.7480 | 1.3090 | 1.7920 | -1.8340 | 2.0600 |
| А,7 | 1.1920 | 1.1830 | 6.7250 | 4.8180 | 0.6310 | 1.0410 | 1.3420 | 1.1640 | 1.4890 | -2.2860 | 1.8940 |
| А,8 | 1.5370 | 1.6390 | -0.5690 | 2.0370 | 0.4540 | -0.1320 | 1.2540 | 0,0390 | 1.5550 | -1.4310 | 1.0640 |
| А,9 | 1.5370 | -0.3990 | -0.5560 | 1.1160 | -0.4780 | 0.0020 | -0.6060 | 0.6480 | 2.1530 | -1.2700 | 1.1970 |
| А,10 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 2.0730 | 0.2070 | 1.3970 |
| А,А | 3.1200 | 3.0230 | 3.5450 | 4.8720 | 2.3070 | 0.0000 | -1.3620 | -0.2430 | 0.2140 | -0.6920 | 3.3340 |
| 2,2 | 4.4790 | 4.8510 | 5.3790 | 13.1380 | 7.3480 | 0.4980 | 1.6370 | 1.6100 | 0.7540 | -1.3140 | 2.8470 |
| 3,3 | 2.2320 | 2.7290 | 11.0750 | 15.4710 | 9.7010 | 0.7020 | -0.4300 | -1.5380 | -0.8700 | -2.4920 | 2.1250 |
| 4,4 | 0.8840 | 1.8800 | 9.1320 | 16.1400 | 9.5290 | 2.4760 | 0.4550 | 0.3380 | 0,0090 | -1.4460 | 2.2100 |
| 5,5 | 7.6550 | 8.7410 | 11.2230 | 16.0940 | 12.6990 | 6.5150 | 3.1720 | 2.6130 | 0.2380 | -1.1510 | 3.7020 |
| 6,6 | 9.8410 | 11.0360 | 14.1250 | 17.1060 | 0.9170 | 2.5610 | -4.4720 | -4.0910 | -0.7110 | -2.2180 | 1.8060 |
| 7,7 | 6.8730 | 8.2850 | 12.1030 | 6.7540 | -1.1240 | -0.3840 | -0.3830 | -3.8370 | -4.2660 | -4.0800 | -0.1170 |
| 8,8 | 4.4530 | 4.2080 | 0.7370 | 2.8160 | -2.4470 | -1.5490 | -3.2240 | -1.2460 | 2.4110 | 2.7050 | 1.0500 |
| 9,9 | 1.0910 | -3.5070 | -1.2560 | 1.3820 | -4.7120 | 0.1480 | -2.4060 | -1.8530 | 3.2860 | 1.0450 | 0.8060 |
| 10,10 | -1.1490 | -1.1970 | -1.4750 | 0.2960 | -0.8740 | -0.7630 | -0.7510 | -1.2620 | 1.6580 | 2.5910 | 0.5780 |
| Общий | 0.9370 | 1.2510 | 2.3110 | 3.6590 | 0.8050 | 0.1970 | -0.3390 | -0.3210 | 0.1480 | -1.7900 | 0.5620 |
Дополнительная литература
Книга Питера Гриффина «Теория блэкджека» наилучшим образом освещает тему этой статьи из всех, что я видел. Он рассматривает этот вопрос в главе 8, озаглавленной «Много колод и разные правила», где используется другой базовый набор правил и рассчитывается разница между одной колодой и бесконечным количеством колод. Он не всегда приводит точные цифры для всего, но перефразирует разбивку разницы в 0,69% при своих предположениях следующим образом:
- Удвоение ставок: почти половина от 0,69%
- Блэкджек среди игроков: 0,07%
- Разделение карт: более чем компенсирует преимущества блэкджека.
- Комментарий к 12-16: «Предположительно, оставшееся расхождение».
Гриффин далее перечисляет преимущества различных изменений правил как для колод с одной колодой, так и для колод с бесконечным количеством карт.
Благодарности
Я хотел бы поблагодарить Дона Шлезингера за его мудрые советы по анализу и корректуре этой статьи.


